Figure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At t=0 the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time. 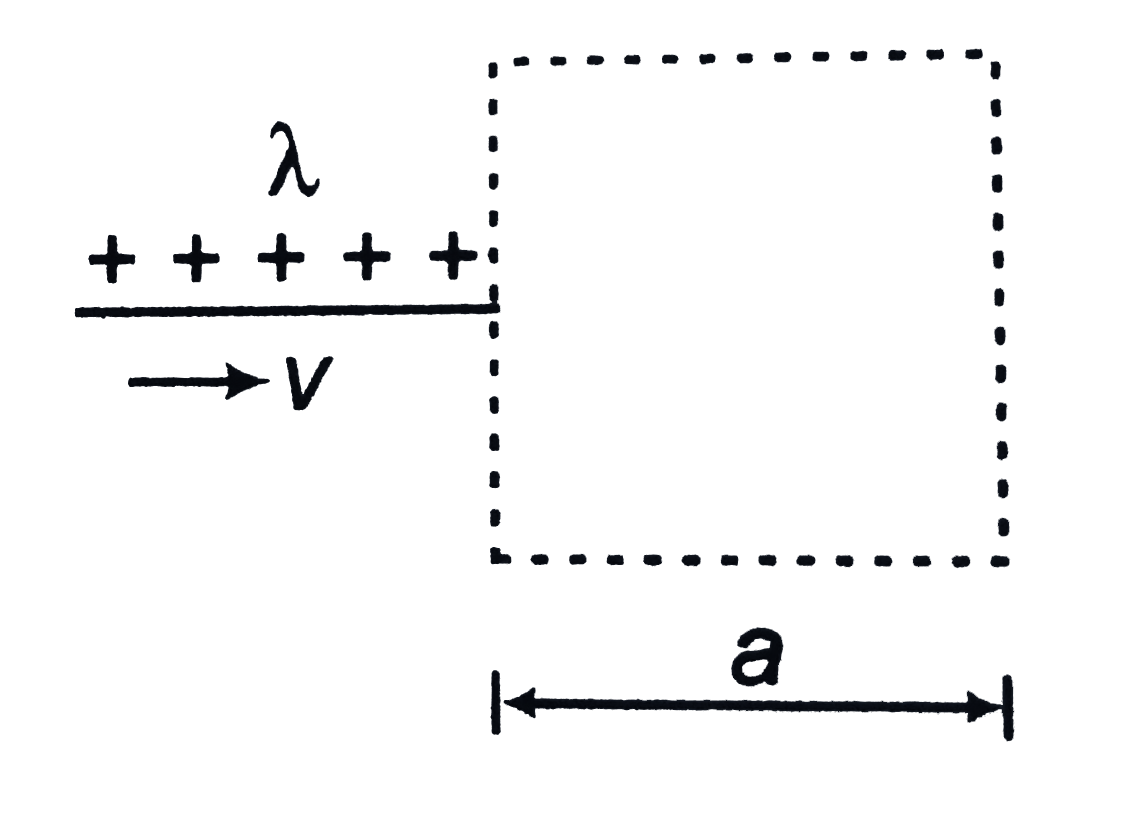
The electric flux passing through a closed surface depends on the net charge inside the surface. Net charge in this case first increases, reaches a maximum value and finaly decreases to zero. The same is the case with the electric flux. The electric flux ϕ versus time graph is as shown in figure below. 
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Exercise 24.1
Explore 4 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Exercise 24.2
Explore 9 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Example Type 8
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
Figure shown an imaginary cube of edge L/2. A uniformly Charged rod of length L moves towards left at a small but constant speed v. At t=0, the left end just touches the centre of the cube opposite it. Which of the graphs shown in figure represents the flux of the electic field through the cube as the rod goes through it?

View SolutionAn imaginary cube of edge length is shown in the figure. A uniformly charged rod having linear charge density and length L moves towards left with constant speed v. At time t = 0, the left end just touches the centre of face of the cube. v= constant Choose the correct graph which represents the flux of the electric field through the cube as rod goes through it. flux- time- flux - time
View Solution
Knowledge Check
The figure shows an imaginary cube of length L/2 and a uniformly charged rod of length L touching the centre of the centre of the right face of the cube normally.At time t=0 the rod starts moving to the left slowly at a constant speed v .The electric flux (F) thriguh the cube si plotted against time (t) .The correct graph showing the variation of flux with time is
 A
A B
B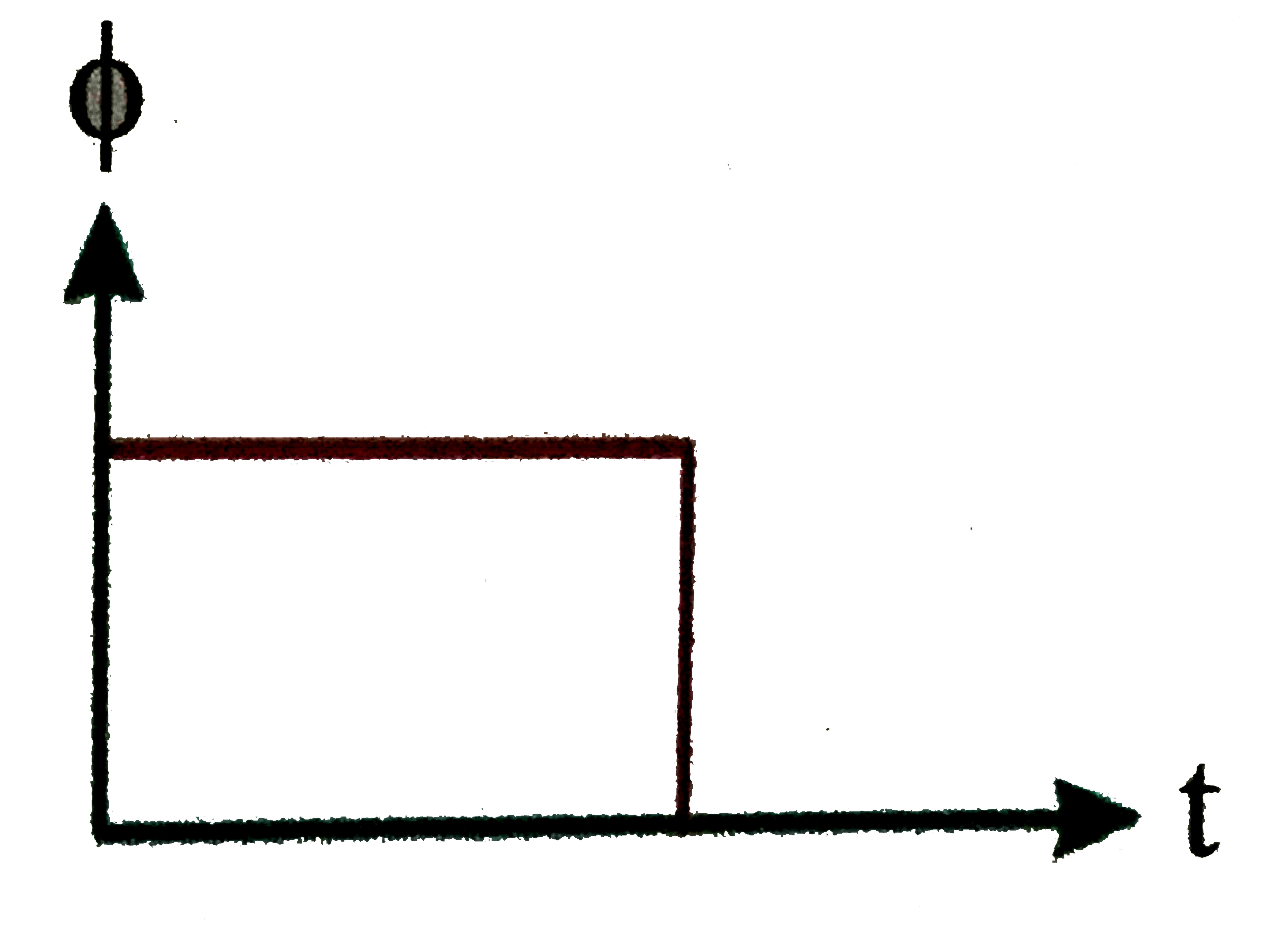 C
C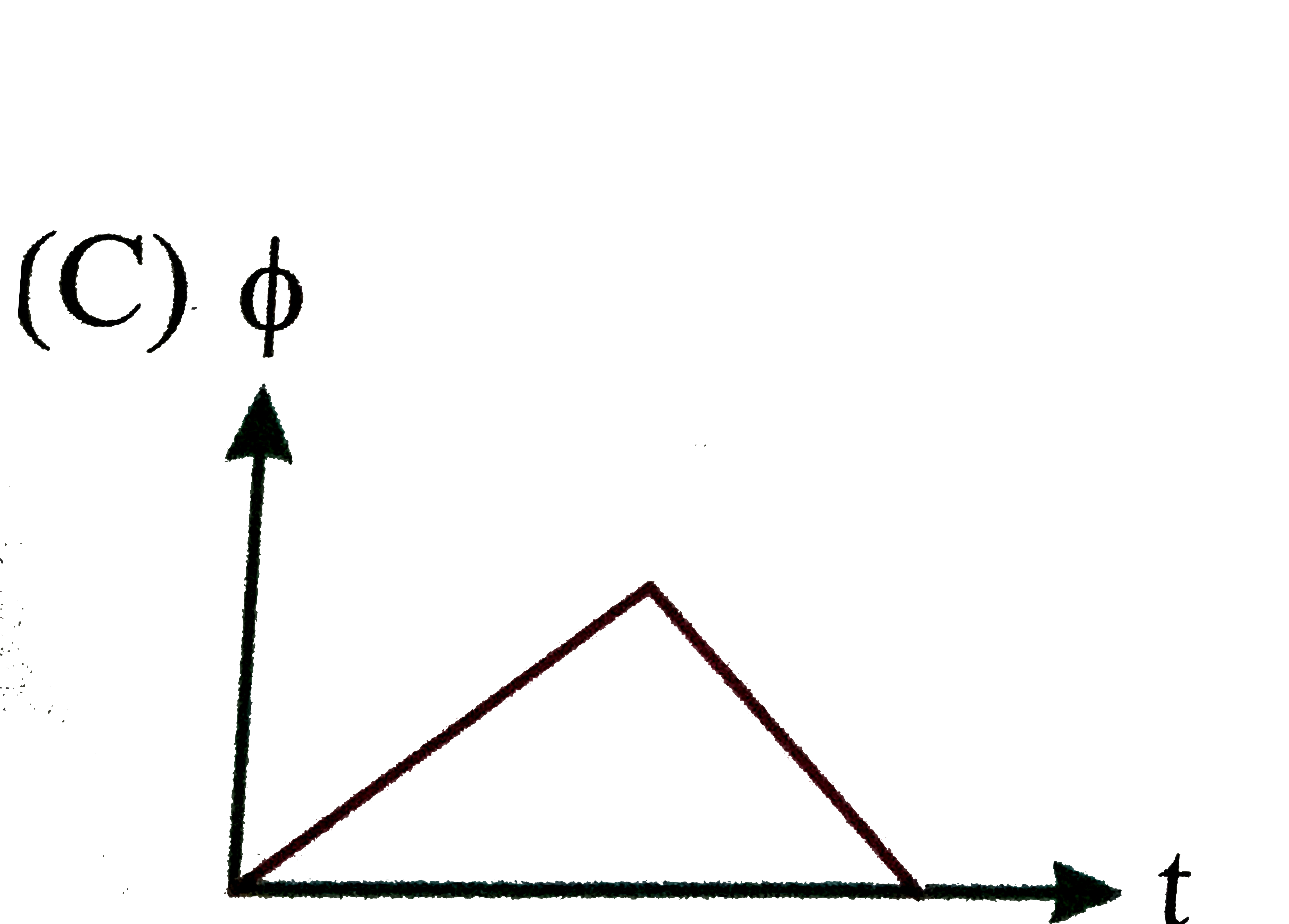 D
D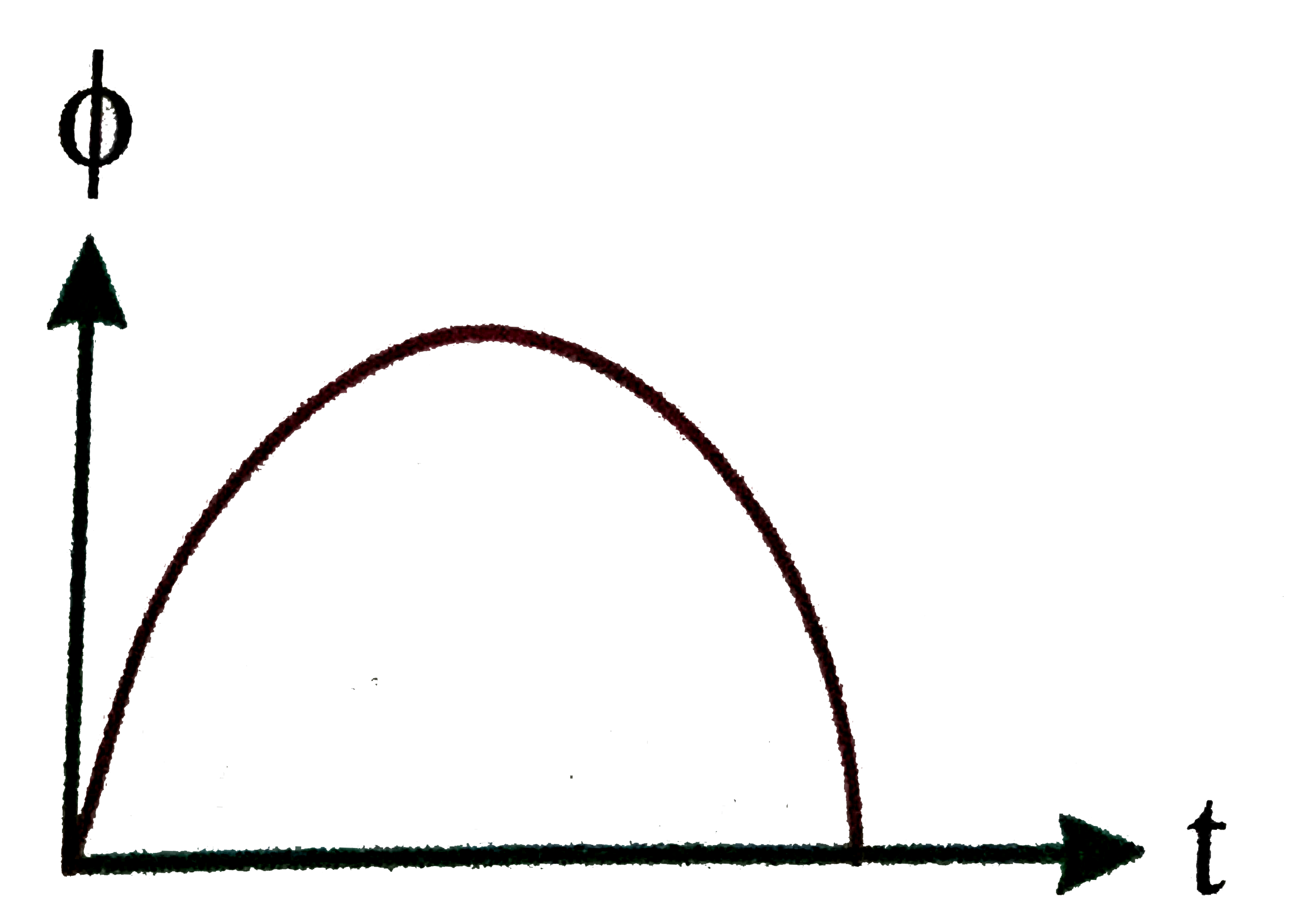
Figure shows a squre loop of side 5 cm being mo ved towards right at a constant speed of 1cm/sec. The front edge just enters the 20 cm wide magnetic field at t=0 . Find the induced emf in the loop at t=2s and t=10s.
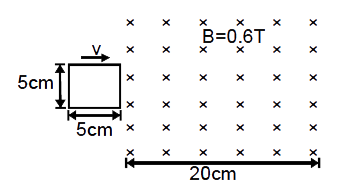 A3×10−2, zeroB3×10−2,3×10−4C3×10−4,3×10−4D3×10−4, zero
A3×10−2, zeroB3×10−2,3×10−4C3×10−4,3×10−4D3×10−4, zeroIn the figure shown as uniform magnetic field |B|=0.5T is perpendicular to the plane of circuit. The sliding rod of length l=0.25m moves uniformly with constant speed v=4ms−1. If the resistance of the sllides is 2Ω, then the current flowing through the sliding rod is
 A0.1AB0.17AC0.08D0.03A
A0.1AB0.17AC0.08D0.03A
A charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionFigure shown a square loop of side l being moved towards right at a constant speed v . The front edge enters th emagnetic field B at t=0 . The width of field is 3l . Sketch induced emf versus time graph.

View SolutionA square loop of side l being moved towards right at a constant speed v as shown in figure. The front edge enters the magnetic field B at t = 0. The width of field is 4l. Sketch induced emf versus time graph.
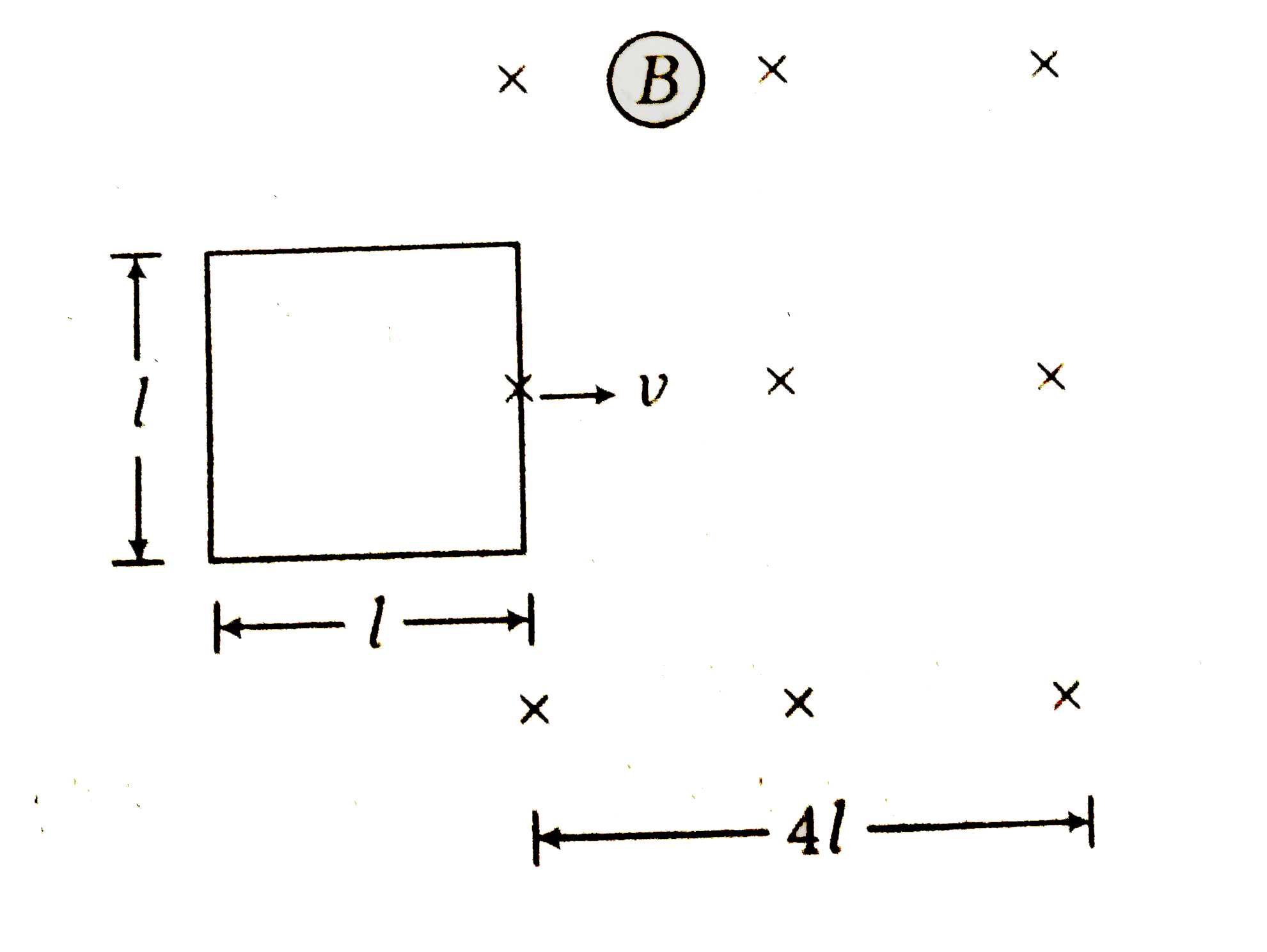
View SolutionA charge Q is uniformly distributed over a rod of length ι. Condider a hypothetical cube of edge ι with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
View SolutionFigure shows a square loop of resistance 1Ω of side 1 m being moved towards right at a constant speed of 1m/s. The front edge enters the 3m wide magnetic field (B=1T) at t=0 . Draw the graph of current induced in the loop as time passes. ( Take anticlockwise direction of current as positive )

View Solution