An electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
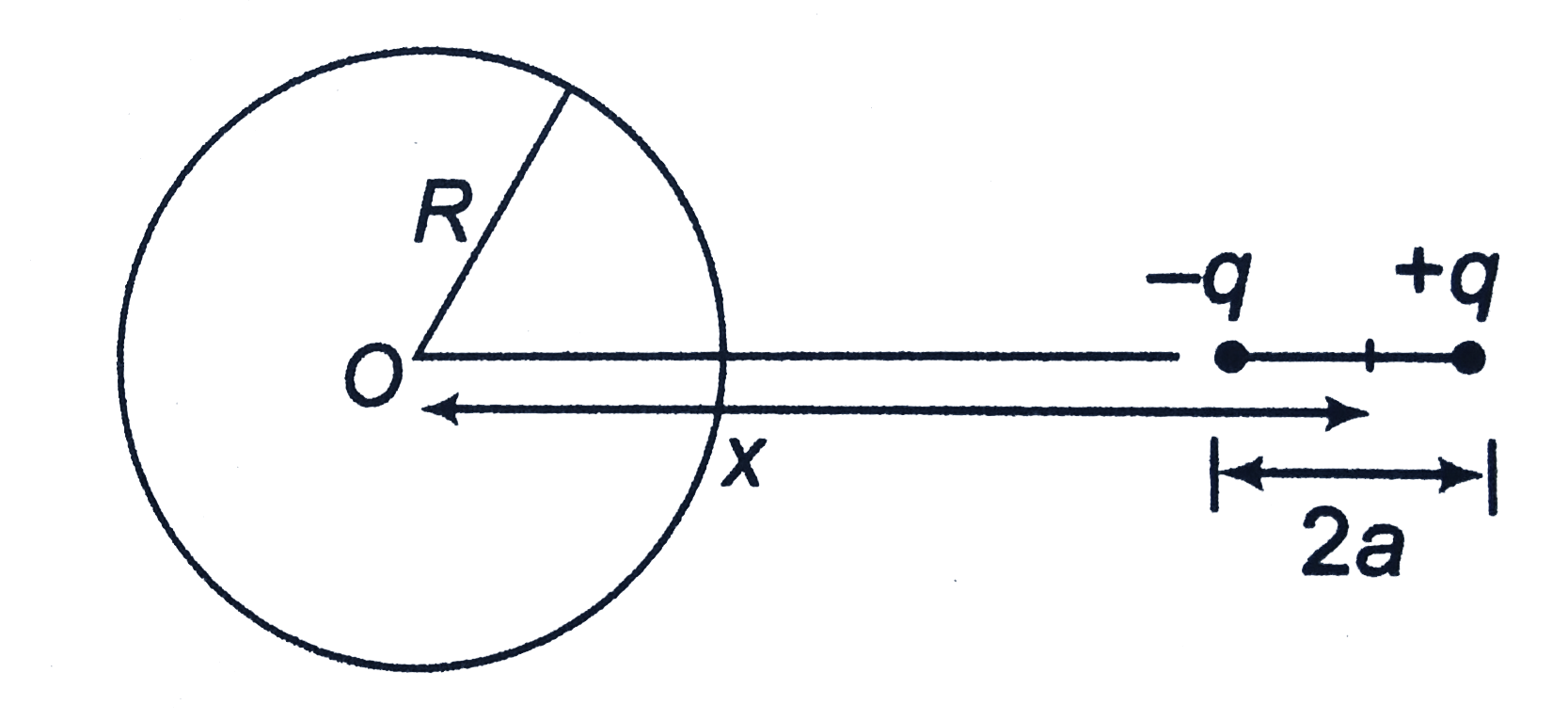
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through ?
The correct Answer is:A, B, C
a.
or
or
Her
b.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
An electric dipole is placed at a distance x from centre O on the axis of a charged ring of radius R and charge Q uniformly distributed over it.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘?
[(a)aqQ2πε0(R2−2x2(R2+x2)3/2),(b)aqQxπε0(R2+x2)3/2]

View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

[(a) (find the net force acting on the dipole b) The work done external agent in rotating the dipole through 180∘ would be
View Solution
Knowledge Check
As shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is
 AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2
AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2
A short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
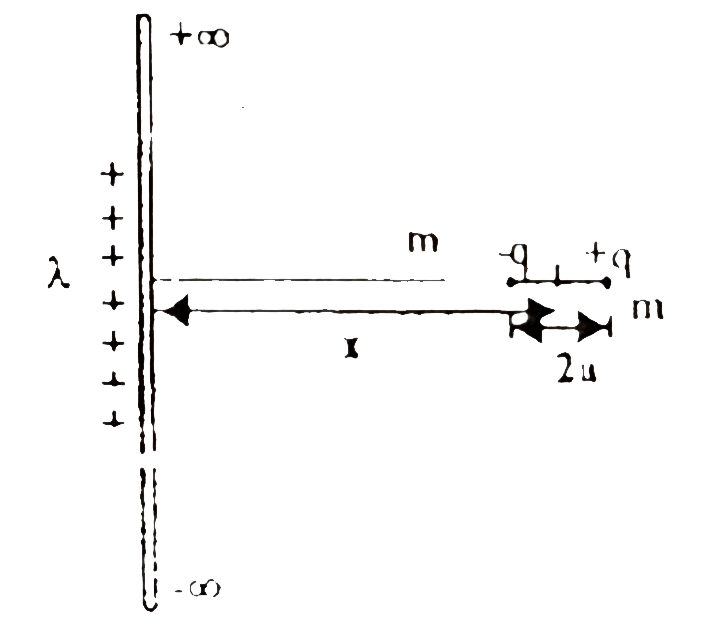
View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.

View SolutionIn figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
[(a)λaqπ∈0x2,(b)2λaqπ∈0x,(c)2π√2π∈0mx2aλq]

View SolutionShort electric dipole of dipole moment P is placed at the centre of a ring of radius R having charge Q uniformly distributed on its circumference. The dipole moment vector is along the axis of the ring. Find force on the dipole due to the ring.
View SolutionA short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

View SolutionA short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

View Solution
