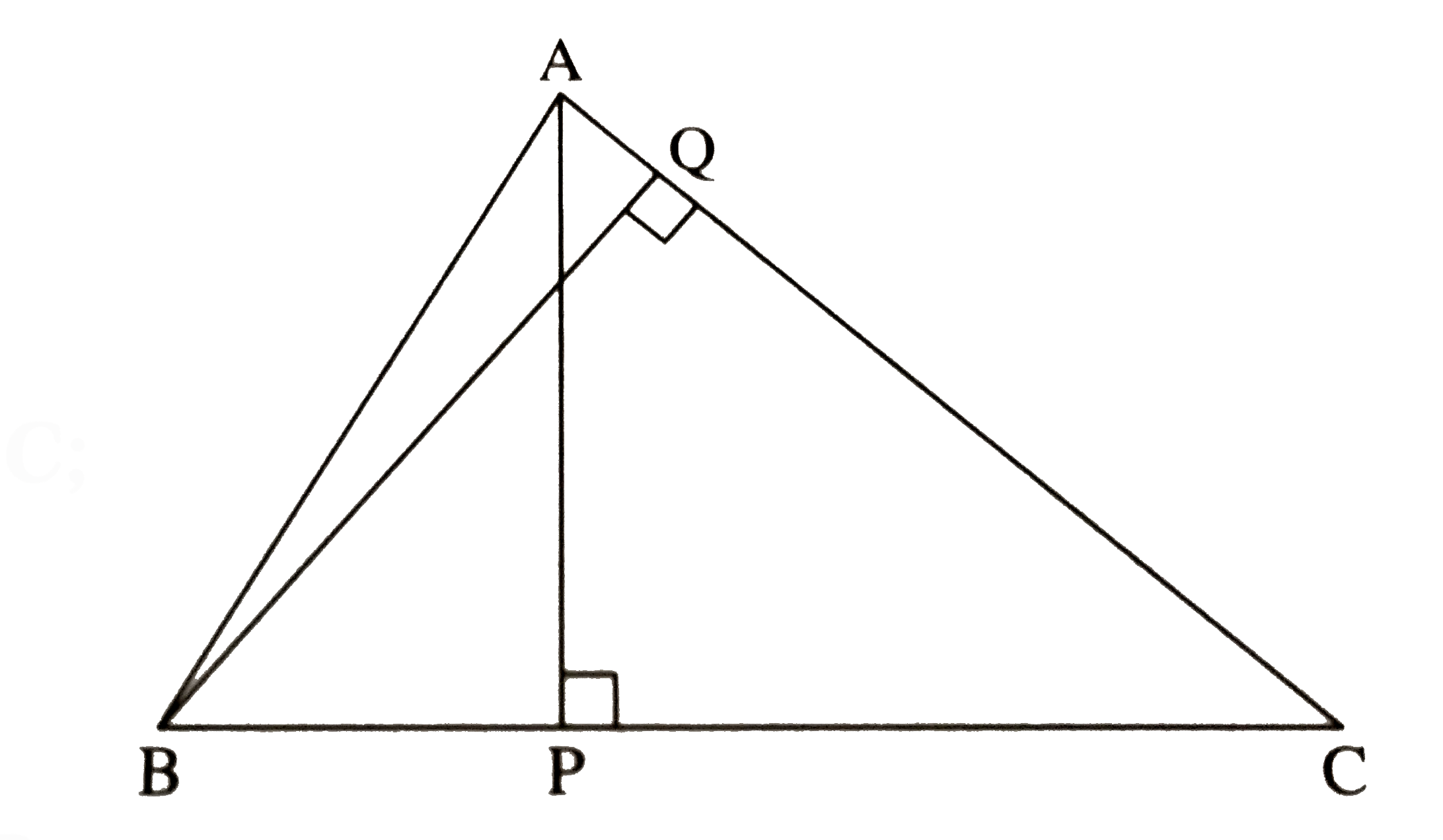
In ΔABC,AP⊥BC,BQ⊥AC.B−P−C,A−Q−C,
then prove that ΔCPA~ΔCQB.
If AP=7,BQ=8,BC=12 then find AC.
Video Solution
Text Solution
In ΔCPA and ΔCQB,
∠CPA≅∠CQB …..(Each of measure 90∘)
∠ACP≅∠BCQ……..(Common angle)
∴ΔCPA~ΔCQB …….. ("AA" test of similarity)
∴APBQ=ACBC ……..(Corresponding sides of similar triangles are proportional)
∴78=AC12.........(Substituting the given values)
∴AC×8=7×12
∴AC=10.5
|
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.3 (2 mark each)
10 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
Knowledge Check
In the ΔABC,AB=a,AC=candBC=b, then
Aa+b+c=0Ba+b-c=0Ca-b+c=0D−a+b+c=0If A:B = 2:3 and B:C = 7:8 then A:C is
A9:11B7:12C16:21Dnone of these
In ΔABC, AP is a median. If AP=7,AB2+AC2=260, then find BC.
View SolutionThe angles A, B and C of a ΔABC are in A.P. If AB=6,BC=7,then AC=
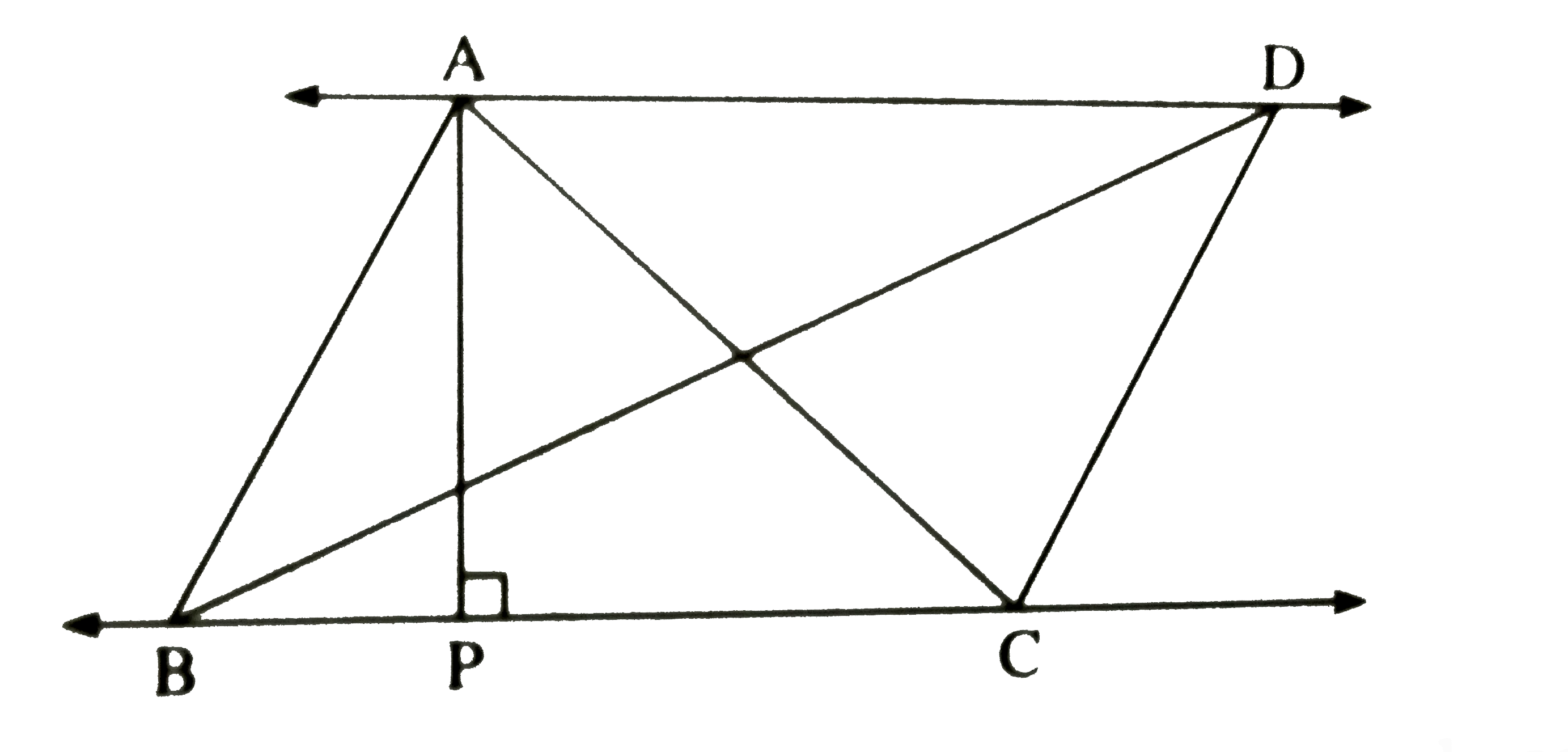
View SolutionIn the following figure AP⊥BC,AD∣∣BC, then find A(ΔABC):A(ΔBCD).
View SolutionIn ΔABC,AC=BCand∠BAC=50∘. Find ∠BCA.
View SolutionIn ΔABC,∠BAC=90∘andAB=AC.Seg AP⊥sBC.B-P-C.Disanyp∮sonsBC.Provetˆ2AD^2=BD^2+CD^2
View SolutionIn ΔABC seg AP is a median. If BC=18,AB2+AC2=260 Find AP.
View Solution
