In an equilateral △ABC,AD is the altitude drawn from A on the side BC. Prove that 3AB2=4AD2
Step by step video & image solution for In an equilateral triangleABC, AD is the altitude drawn from A on the side BC. Prove that 3AB^(2) = 4AD^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.5
5 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 1 MARK MULTIPLE CHOICE QUESTIONS )
11 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.3
9 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.4
12 Videos
- QUADRATIC EQUATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS
2 Videos
Similar Questions
The perimeters of two similar triangles are 25cm and 15cm respectively. If one side of the first triangle is 9cm, find the length of the corresponding side of the second triangle.
OR
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD2=7AB2
View SolutionIn an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD2 is equal to
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn equilateral △ABC,AD⊥BC. Prove that 3BC2=4AD2.
View SolutionAD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
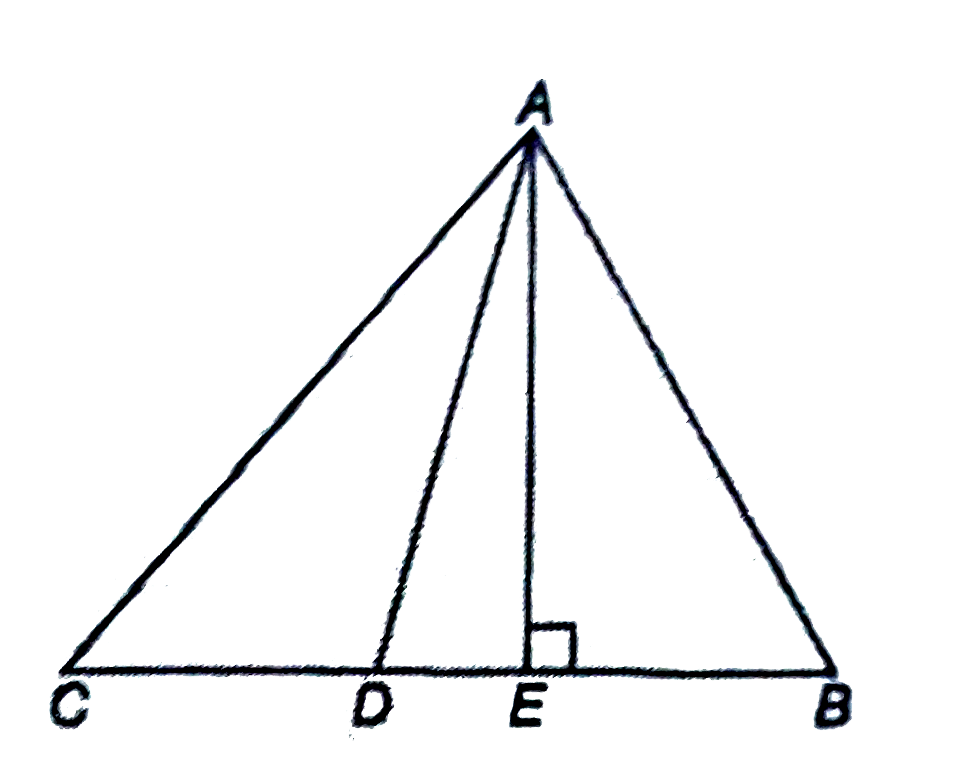
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionIn an equilateral triangle with side a, prove that the altitude is of length a√32
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View SolutionIn an equilateral triangle ABC the side BC is trisected at D . Prove that 9 AD2=7 AB2
View SolutionIn a ΔABC, altitude drawn from vertex A to side BC meets BC at D such that DB=3CD. Prove that 2AB2=2AC2+BC2
View Solution
