1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
Step by step video & image solution for 1. In the figure trianglePQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN^2 = 3PR^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

View SolutionIn the figure 2.35,ΔPQR is an equilatral triangle. Point S is on seg QR such that QS=13QR. Prove that : 9PS2=7PQ2
View SolutionIn the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
View SolutionIn the given figure, ABC is an equilateral triangle; PQ∣∣AC and AC is produced to R such that CR=BP. Prove that QR bisects PC
View SolutionIn the givne figure, ABC is an equilateral triangle, PQ||AC and AC is produced to R such that CR = BP. Prove that QR bisects PC.

View SolutionIn the figure given below, ΔPQR is right-angled at Q and the points S and T trisect the side QR. Prove that 8PT2=3PR2+5PS2
View SolutionIf PQR is an equilateral triangle and PX ⊥ QR, find the value of PX^2.
View SolutionIn figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.

View SolutionIn the figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
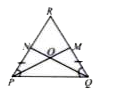
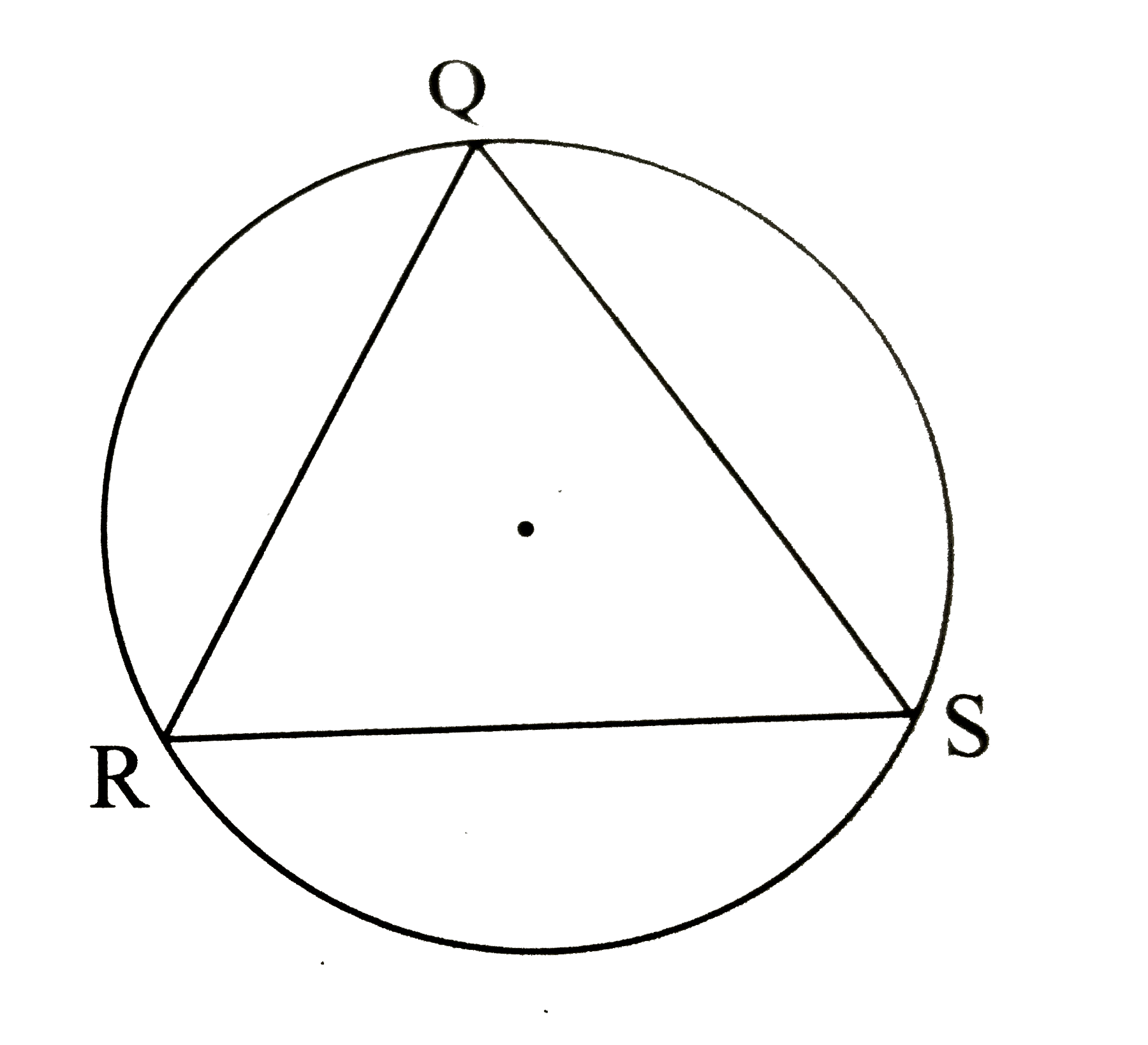
View SolutionIn the figure , ΔQRS is an equilateral triangle.
Prove that
(1) arc RS ≅arcQS≅ arc QR
(2) m (arc QRS ) =240∘.
Proof :
View Solution
