If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70∘, then ∠POA is equal to
70∘
55∘
100∘
40∘
The correct Answer is:B
To solve the problem, we need to find the angle ∠POA given that the tangents PA and PB from point P to the circle with center O are inclined to each other at an angle of 70∘.
1. Draw the Circle and Tangents:
- Draw a circle with center O.
- Mark a point P outside the circle.
- Draw two tangents PA and PB from point P to the circle, touching the circle at points A and B respectively.
2. Identify the Given Angle:
- We are given that the angle between the tangents PA and PB is ∠APB=70∘.
3. Use the Properties of Tangents:
- Recall that the radius of the circle is perpendicular to the tangent at the point of contact. Therefore, ∠OAP=90∘ and ∠OBP=90∘.
4. Form a Quadrilateral:
- Consider the quadrilateral OAPB. The sum of the angles in any quadrilateral is 360∘.
- We can express the angles as follows:
∠OAP+∠APB+∠OBP+∠AOB=360∘
- Substituting the known values:
90∘+70∘+90∘+∠AOB=360∘
5. Solve for ∠AOB:
- Combine the known angles:
90+70+90=250∘
- Therefore,
250∘+∠AOB=360∘
- Solving for ∠AOB:
∠AOB=360∘−250∘=110∘
6. Find ∠POA:
- The angle ∠POA is half of ∠AOB because PA and PB are tangents from point P to the circle.
- Therefore,
∠POA=12∠AOB=110∘2=55∘
Final Answer:
Thus, ∠POA=55∘.
- Draw a circle with center O.
- Mark a point P outside the circle.
- Draw two tangents PA and PB from point P to the circle, touching the circle at points A and B respectively.
- We are given that the angle between the tangents PA and PB is ∠APB=70∘.
- Recall that the radius of the circle is perpendicular to the tangent at the point of contact. Therefore, ∠OAP=90∘ and ∠OBP=90∘.
- Consider the quadrilateral OAPB. The sum of the angles in any quadrilateral is 360∘.
- We can express the angles as follows:
∠OAP+∠APB+∠OBP+∠AOB=360∘
- Substituting the known values:
90∘+70∘+90∘+∠AOB=360∘
- Combine the known angles:
90+70+90=250∘
- Therefore,
250∘+∠AOB=360∘
- Solving for ∠AOB:
∠AOB=360∘−250∘=110∘
- The angle ∠POA is half of ∠AOB because PA and PB are tangents from point P to the circle.
- Therefore,
∠POA=12∠AOB=110∘2=55∘
Thus, ∠POA=55∘.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.26videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.311videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)7videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80o then ∠POA is equal to 50o (b) 60o (c) 70o (d) 80o
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View Solution
Knowledge Check
- Question 1 - Select One
If tangent PA and PB from a point P to a circle with centre O are inclined to each other at angle 80∘, then ∠POA is equal to
A50∘B60∘C70∘D80∘
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 110∘ , find ∠POA.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘ , then find ∠POA .
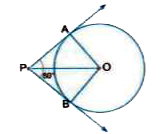 View Solution
View SolutionTwo tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
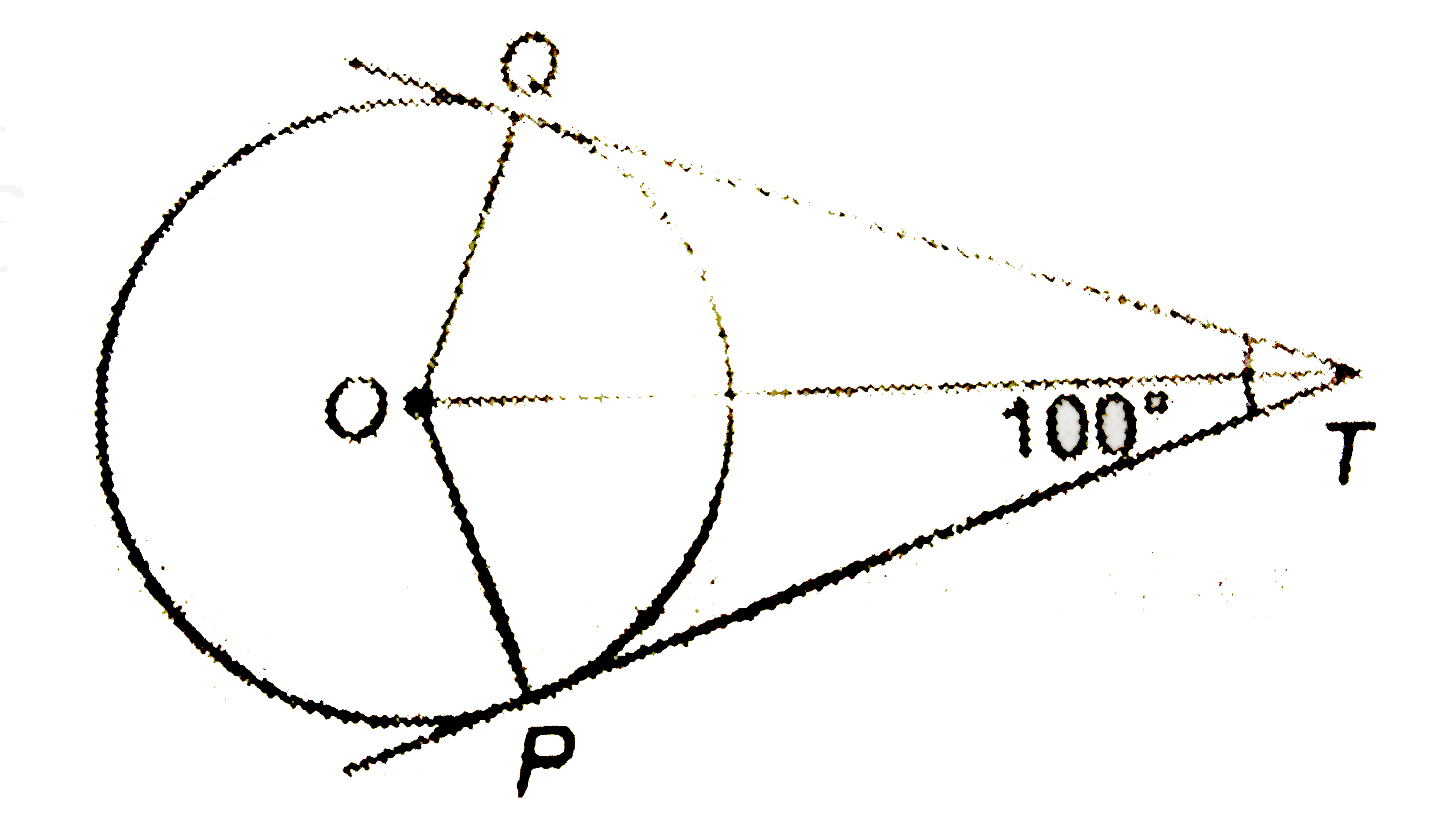 View Solution
View SolutionIf PA and PB are tangents drawn from an external point P to a circle with centre O such that ∠APB=70∘, then ∠OAB is equal to:
यदि PA और PB एक बाहरी बिंदु P से केंद्र O के साथ एक वृत्त में खींची गई स्पर्श रेखाएँ हैं जैसे कि ∠APB=70∘ तो ∠OAB बराबर है:View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=80∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=80∘ है, तो ∠OAB का मान क्या होगा ?View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100o , then what is the value of ∠POQ ?
View Solution

