A 4 A current carrying loop consists of three identical quarter circles of radius 5 cm lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin joined together, value of B at the origin is
μ010(ˆi+ˆj−ˆk)T
μ010(−ˆi+ˆj+ˆk)T
μ05(ˆi+ˆj+ˆk)T
10μ0(ˆi+ˆj+ˆk)T
The correct Answer is:D
As →B=→Bxy+→Byz+→Bzx …(i)
where →Bxy=μ04πIRθˆk,→Byz=μ04πIRθˆi,→Bzx=μ04πIRθˆj,
Substituting these values in equation (i) we get,
→B=μ04πIRθ(ˆi+ˆj+ˆk)
Here, θ=π2,I=4A and R = 5 cm =5×10−2m
∴ →B=μ04πIRθ[ˆi+ˆj+ˆk]
Here, θ=π2,I=4AandR=5cm=5×10−2m
∴ →B=μ04π×45×10−2×π2(ˆi+ˆj+ˆk)=10μ0(ˆi+ˆj+ˆk)T
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Ampere'S Circuit Law
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - The Solenoid And The Toroid
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Magnetic Field Due To A Current Element, Biot-Savart Law
4 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason
15 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View SolutionThe line y=√3x+4 touches a circle with centre at the origin. Find the radius of the circle.
View Solution
Knowledge Check
A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
Aμ0i2√2RBμ0i2RCμ0i4RDμ0i√2RA current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-y plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
Aμ0i2√2RBμ0i2RCμ0i4RDμ0i√2RA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.
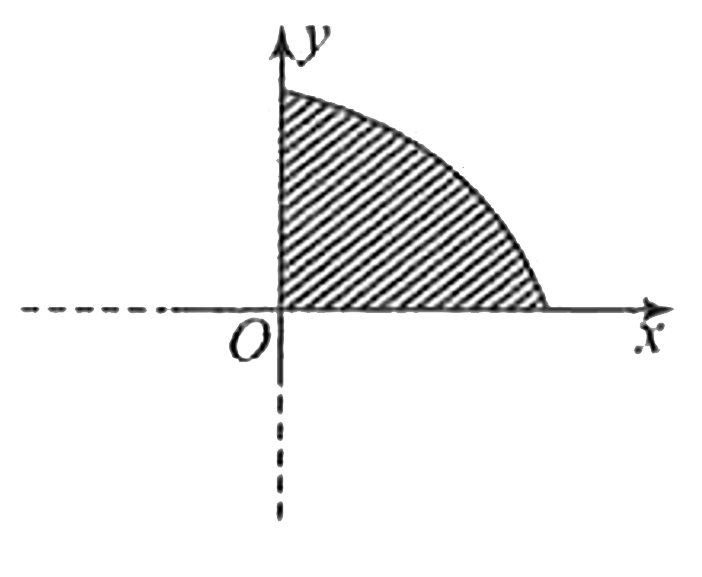
A uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).
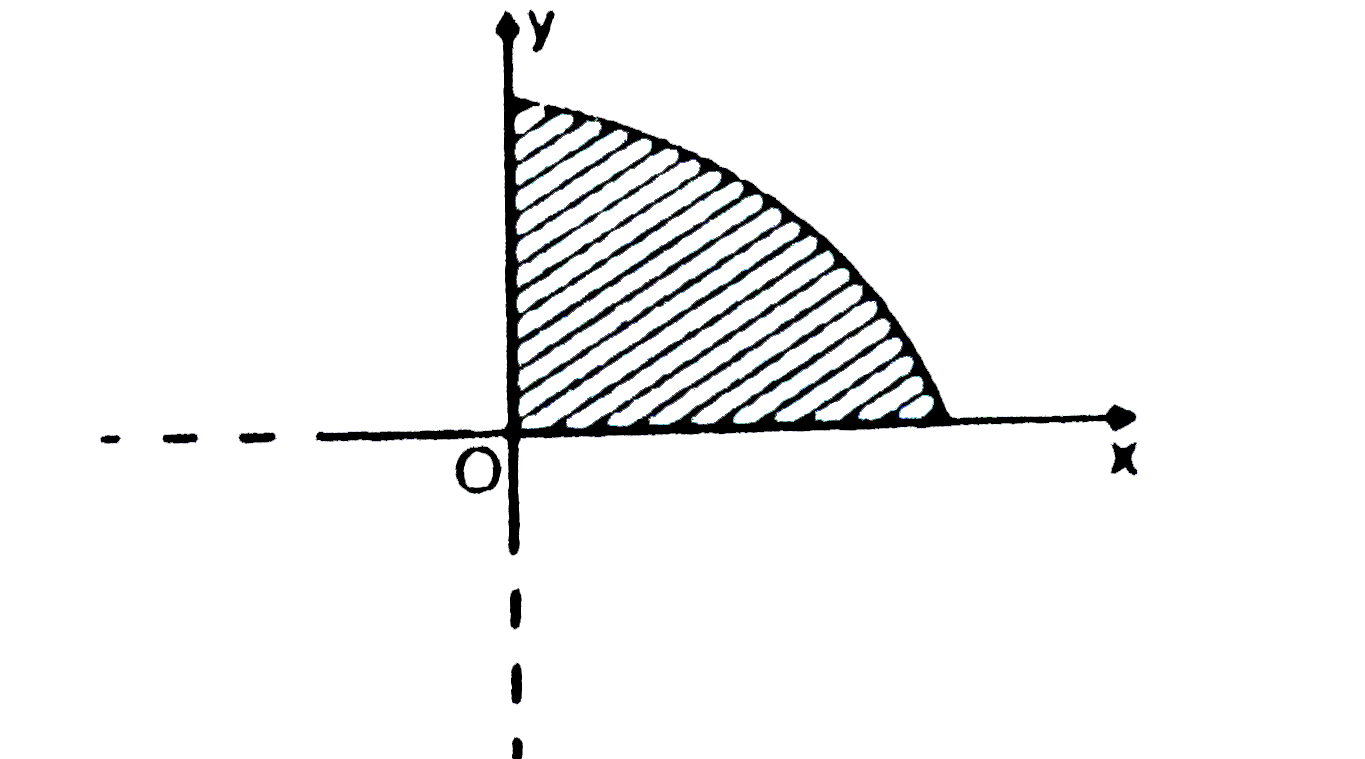
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
View SolutionVerify the Ampere's law for magnetic field of a point dipole moment →M=Mˆk. Take C as the closed curve running clockwise along (i) z-axis from z=a>0 to z=R, (ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane, (iii) along the x-axis from x=R to x=a, and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-y plane.
View SolutionThe distance of the plane 3x+4y+5z=10 from the origin is:
View SolutionAn equation of a plane parallel to the plane x−2y+2z−5=0 and at a unit distance from the origin is
View Solution
