The electric current in a circular coil of two turns produced a magnetic induction of 0.2 T at its centre. The coil is unwound and then rewound into a circular coil of four turns. If same current flows in the coil, the magnetic induction at the centre of the coil now is
0.2T
0.4T
0.6T
0.8T
The correct Answer is:D
To solve the problem, we need to determine the magnetic induction at the center of a circular coil after it has been rewound into a coil with a different number of turns. Let's break down the solution step by step.
Step 1: Understand the relationship between magnetic induction, number of turns, and current.
The magnetic induction B at the center of a circular coil is given by the formula:
B=μ0nI2R
where:
- B is the magnetic induction,
- μ0 is the permeability of free space,
- n is the number of turns,
- I is the current flowing through the coil,
- R is the radius of the coil.
Step 2: Set up the equations for the two scenarios.
For the first coil with n1=2 turns, the magnetic induction B1 is given as 0.2 T. Thus, we can write:
B1=μ0n1I2R1=0.2T
For the second coil with n2=4 turns, we need to find the new magnetic induction B2:
B2=μ0n2I2R2
Step 3: Relate the lengths of wire used in both coils.
The length of the wire used in both coils remains the same. The length of the wire L for the first coil is:
L=n1⋅2πR1=2⋅2πR1=4πR1
For the second coil:
L=n2⋅2πR2=4⋅2πR2=8πR2
Since the lengths are equal, we can equate them:
4πR1=8πR2
From this, we can simplify to find the relationship between R1 and R2:
R2=R12
Step 4: Substitute R2 into the equation for B2.
Now we can substitute R2 into the equation for B2:
B2=μ0n2I2R2=μ0⋅4I2⋅(R12)=μ0⋅4IR1
Step 5: Relate B2 to B1.
Now we can relate B2 to B1:
B1=μ0⋅2I2R1=μ0IR1
Thus, we can express B2 in terms of B1:
B2=4⋅B1
Step 6: Calculate B2.
Given that B1=0.2T:
B2=4⋅0.2T=0.8T
Final Answer:
The magnetic induction at the center of the coil with 4 turns is 0.8T.
---
The magnetic induction B at the center of a circular coil is given by the formula:
B=μ0nI2R
where:
- B is the magnetic induction,
- μ0 is the permeability of free space,
- n is the number of turns,
- I is the current flowing through the coil,
- R is the radius of the coil.
For the first coil with n1=2 turns, the magnetic induction B1 is given as 0.2 T. Thus, we can write:
B1=μ0n1I2R1=0.2T
B2=μ0n2I2R2
The length of the wire used in both coils remains the same. The length of the wire L for the first coil is:
L=n1⋅2πR1=2⋅2πR1=4πR1
L=n2⋅2πR2=4⋅2πR2=8πR2
4πR1=8πR2
From this, we can simplify to find the relationship between R1 and R2:
R2=R12
Now we can substitute R2 into the equation for B2:
B2=μ0n2I2R2=μ0⋅4I2⋅(R12)=μ0⋅4IR1
Now we can relate B2 to B1:
B1=μ0⋅2I2R1=μ0IR1
Thus, we can express B2 in terms of B1:
B2=4⋅B1
Given that B1=0.2T:
B2=4⋅0.2T=0.8T
The magnetic induction at the center of the coil with 4 turns is 0.8T.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTIPSChapter:MOVING CHARGES AND MAGNETISM Exercise:Ampere'S Circuit Law
Explore 5 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTIPSChapter:MOVING CHARGES AND MAGNETISM Exercise:The Solenoid And The Toroid
Explore 5 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTIPSChapter:MOVING CHARGES AND MAGNETISM Exercise:Magnetic Field Due To A Current Element, Biot-Savart Law
Explore 4 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTIPSChapter:MAGNETISM AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
- NUCLEIBook:NCERT FINGERTIPSChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
When a long wire carrying a steady current is best into a circular coil of one turn, the magnetic induction at its centre is B. When the same wire carrying the same current is bent into a circular coil of one turn, the magnetic induction at its centre is B. when the same wire carrying the same current is bent to form a circular coil of a turns of a smaller radius, the magnetic induction at the centre will be
View SolutionA wire length 6.28m is bent into a circular coil of 2 turns. If a current of 0.5A exists in the coil, the magnetic moment of the coil is, in Am2:
View Solution
Knowledge Check
The current passing through a circular coil of two rurns produces a magnetic firld of 4μT as its centre. The coil is then rewound, so as to have four turns and the current passing through it is doubled. What is the new magnetic firld at the centre of the coil ?
A8μTB16μTC24μTD32μTA current passing through a circular coil of two turns produces a magnetic field B as its centr. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is
A2BBB/2CB/4D4BA wire length 6.28m is bent into a circular coil of 2 turns. If a current of 0.5A exists in the coil, the magnetic moment of the coil is, in Am2:
Aπ4B14CπD4π
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
View SolutionA circular coil carrying a certain, current produces a magnetic field B0 at its centre. The coil is now rewound so a to have 3 turns and the same currents is passed through it. The new magnetic field at the centre is
View SolutionA circular coil carrying a certain current produces a megnetic field Bo at its centre. The coil is now rewound so as to have 3 turns and the same current is passed through it. The new magnetic field at the centre is
View SolutionA circular coil of length L and radius r carries a current I. It provides a magnetic field of induction B at its center. Now the coil is bent sharply so as from a circular coil of n turns of rqual radii. The new induction at the center of this coil is
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
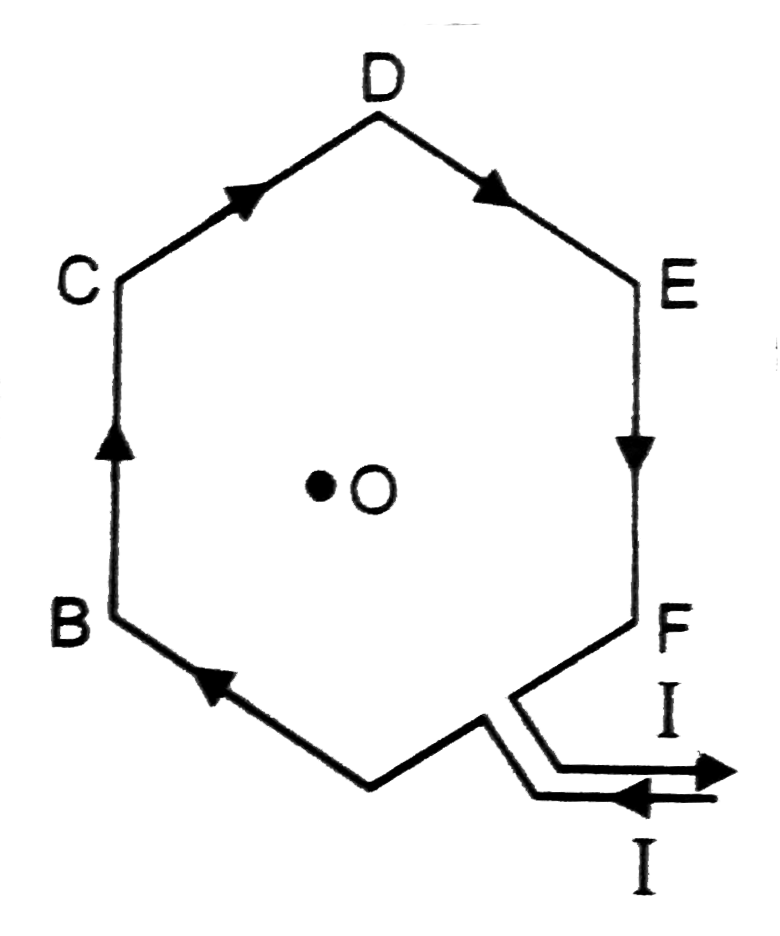
View Solution
