ABCD is a regular tetrahedron. MandN are the mid points of the edges ABandCD. It the length of AB is a, then ∣∣¯¯¯¯¯¯¯¯MN∣∣2=
Step by step video & image solution for ABCD is a regular tetrahedron. M and N are the mid points of the edges AB and CD. It the length of AB is a, then |bar(MN)|^2 = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
ABCD is a regular tetrahedron P & Q are the mid -points of the edges AC and AB respectively, G is the cenroid of the face BCD and θ is the angle between the vectors −−→PG and −−→DQ, then
View SolutionIn a regular tetrahedron, if the distance between the mid points of opposite edges is unity, its volume is
View Solution
Knowledge Check
ABCD is a regular tetrahedron P & Q are the mid -points of the edges AC and AB respectively, G is the cenroid of the face BCD and θ is the angle between the vectors −−→PG and −−→DQ, then
AThe angle between −−→AB and −−→CD is 90∘BThe angle θ is π−cos−1(53√3)CThe angle θ is π−cos−1(56√3)DThe angle between −−→AB and −−→CD is 120∘In a regular tetrahedron, if the distance between the mid points of opposite edges is unity, its volume is
A13B12C1√2D16√2M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NM
ABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:

View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
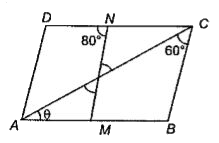
View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is

View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :

View SolutionABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
View Solution