In figure, the vertices, of square DEFG are on the sides of ΔABC. ∠A=90∘. Then prove that DE2=BD×EC.
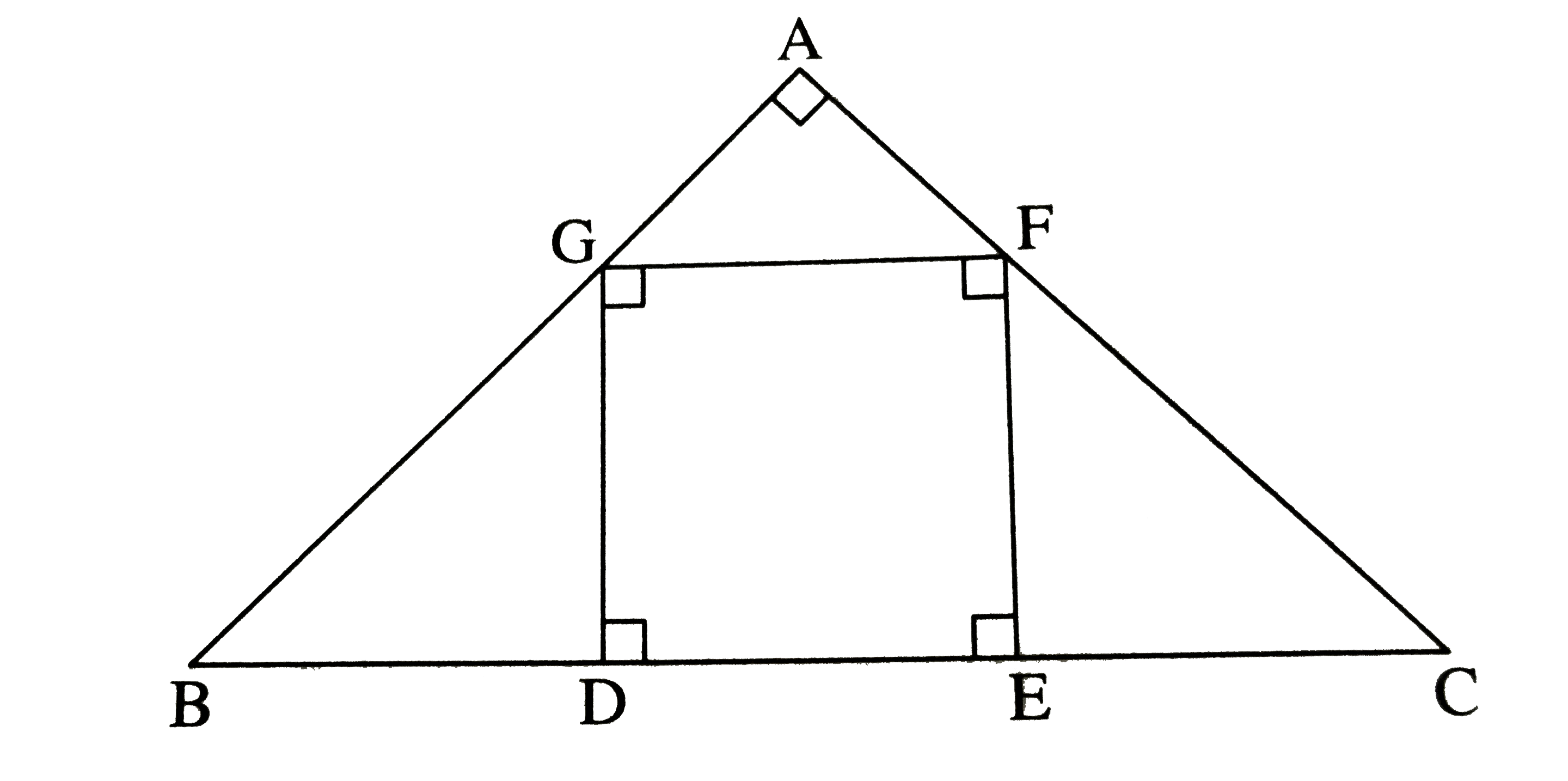
□DEFG is a square (Given)
∴DE=EF=GF=GD
………….(Sides of a square )………….1
∠GDE=∠DEF=90∘………….(Angles of a square)
∴ seg GD⊥ sides BC and seg EF⊥ side BC
In ΔBAC and ΔBDG,
∠BAC≅∠BDG….......(Each measures 90∘)
∠ABC≅∠DB (Common angles)
∴ΔBAC~ΔBDG ...........(AA test of similarity) .......2
Similarly ΔBAC~ΔFEC.......3
∴ΔBDG~ΔFEC ...........[From 2 and 3]
∴BDEF=GDEC.............(Corresponding sides of similar triangles are in proportion)
∴BDDE=DEEC............[From 1]
∴DE2=BD×EC.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE15videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)3videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
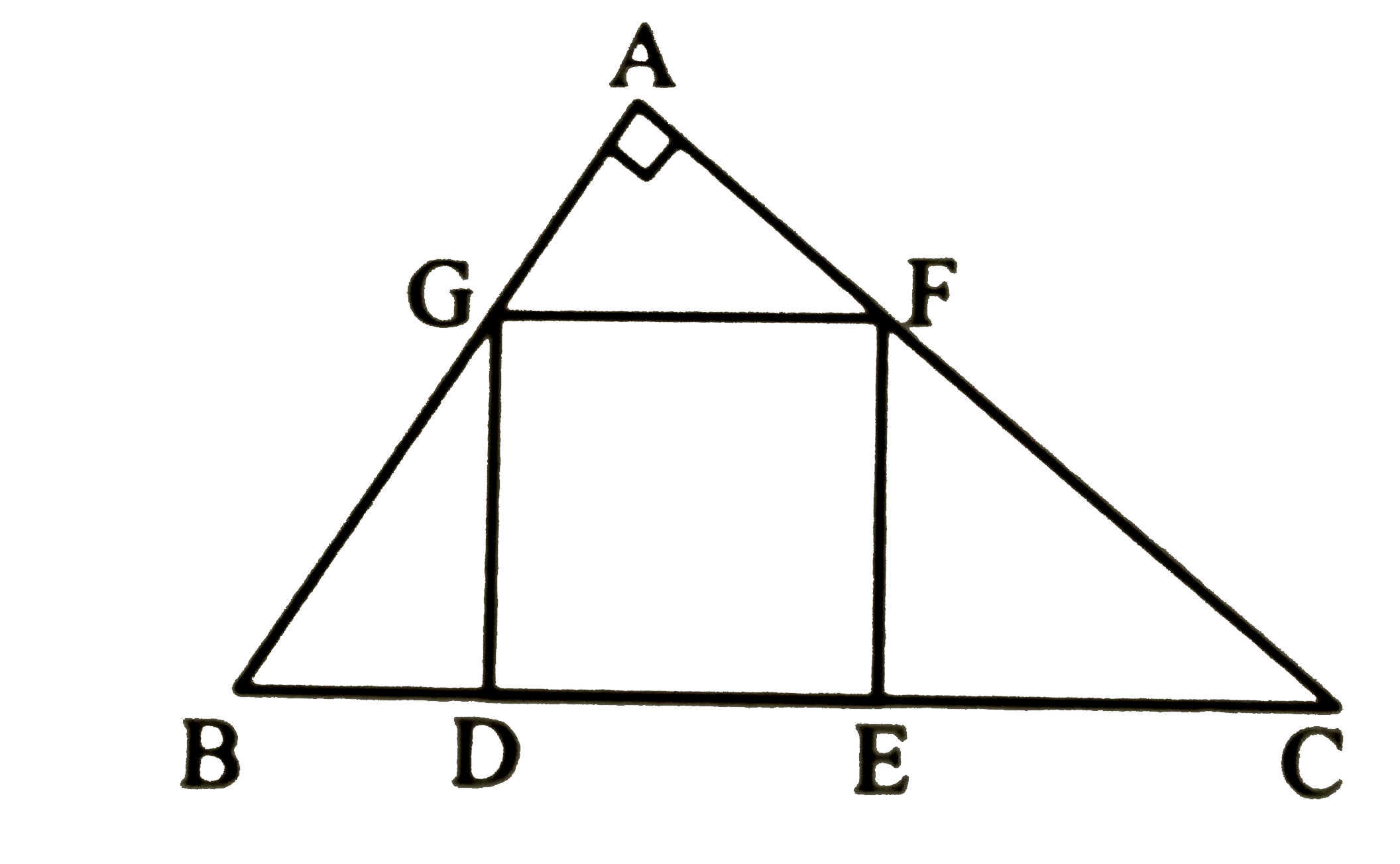
In the adjoining figure, the vertices of square DEFG are on the sides of ΔABC. If ∠A=90∘, then prove that DE2=BD×EC.
 View Solution
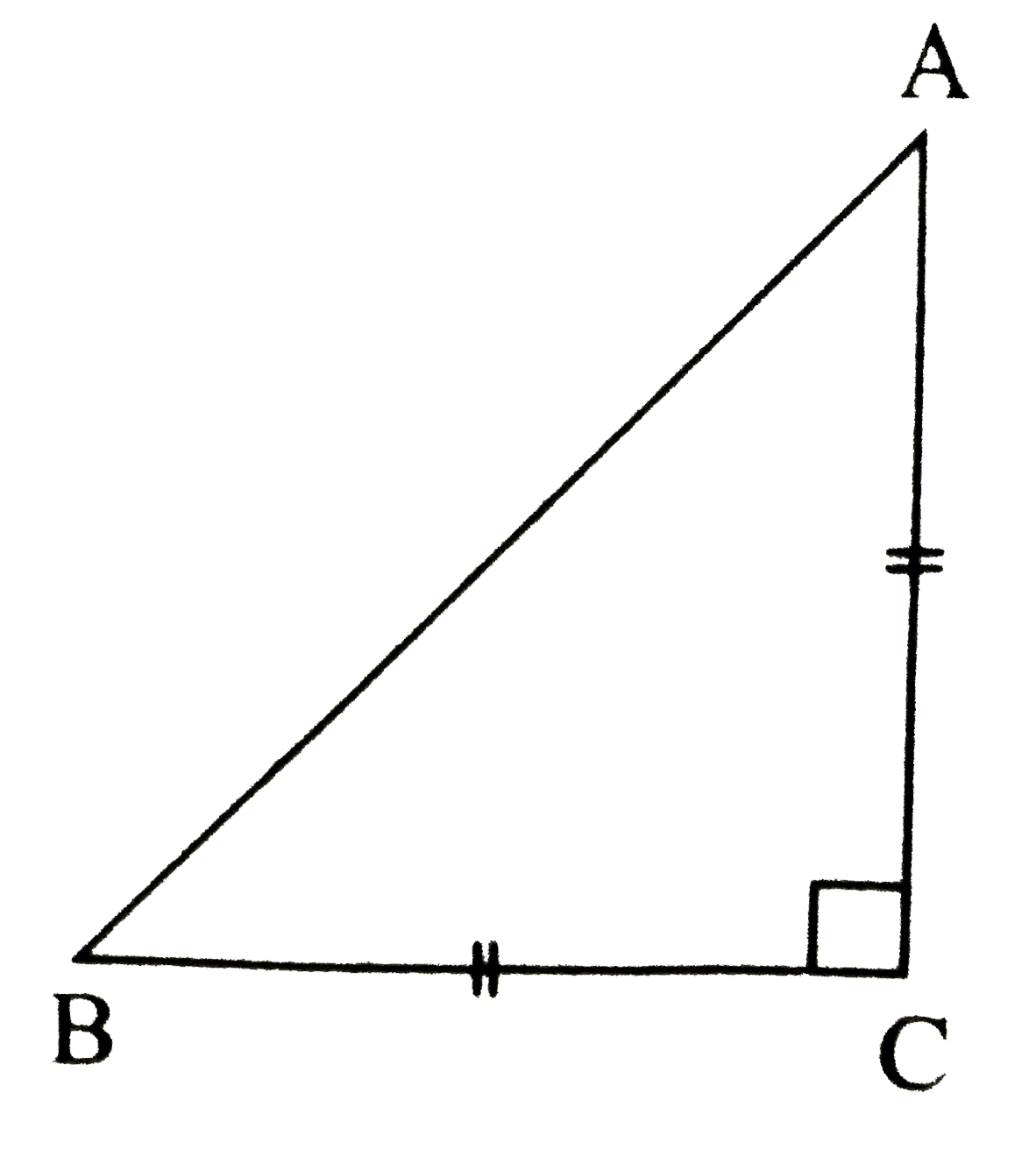
View SolutionIn ΔABC, AC=BC and ∠ACB=90∘ then prove AB2=2AC2
 View Solution
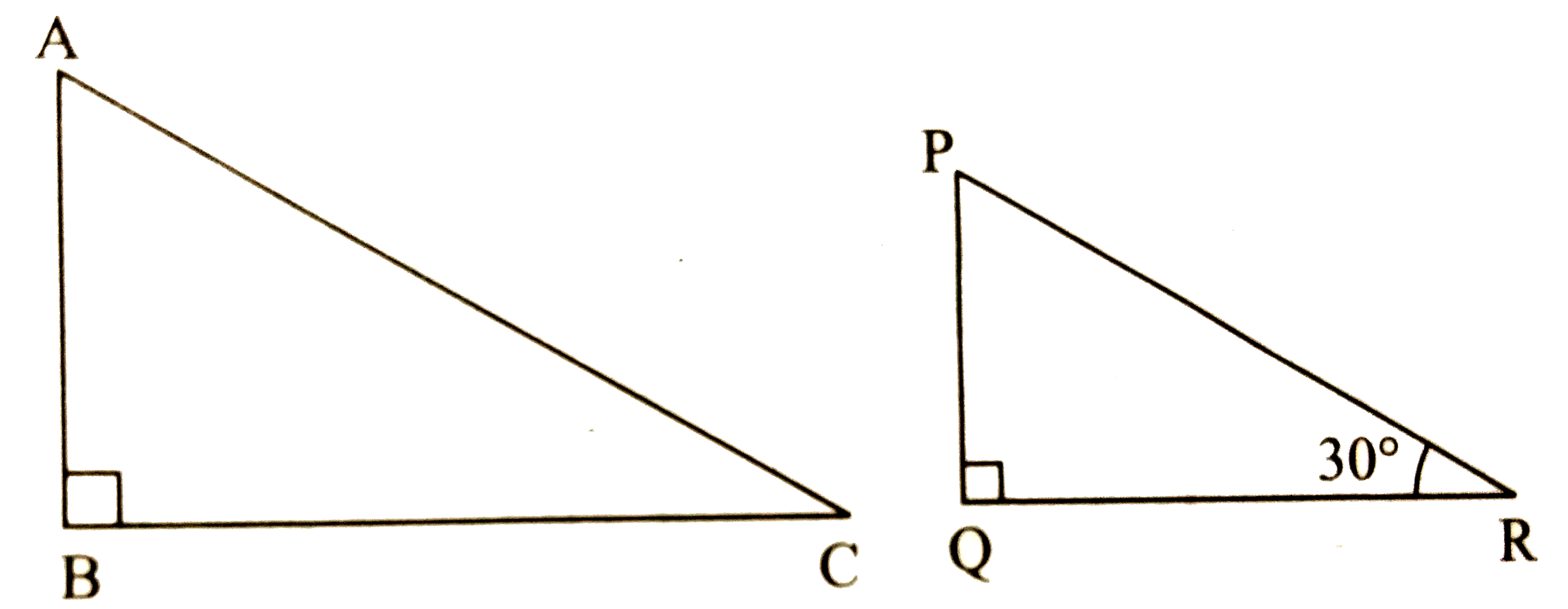
View SolutionIn the figure, ΔABC~ΔPQR ∠R=30∘, then ∠A=?
 View Solution
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that AC2+BD2=AD2+BC2.
View SolutionIn figure∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
View SolutionIn the given figure DEFG is a square and ∠BAC=90∘ . Show that FG2=BG×FC .
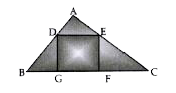 View Solution
View SolutionIn the figure in ΔABC, point D on side BC is such that ∠BAC=∠ADC.
Prove that CA2=CB×CD.
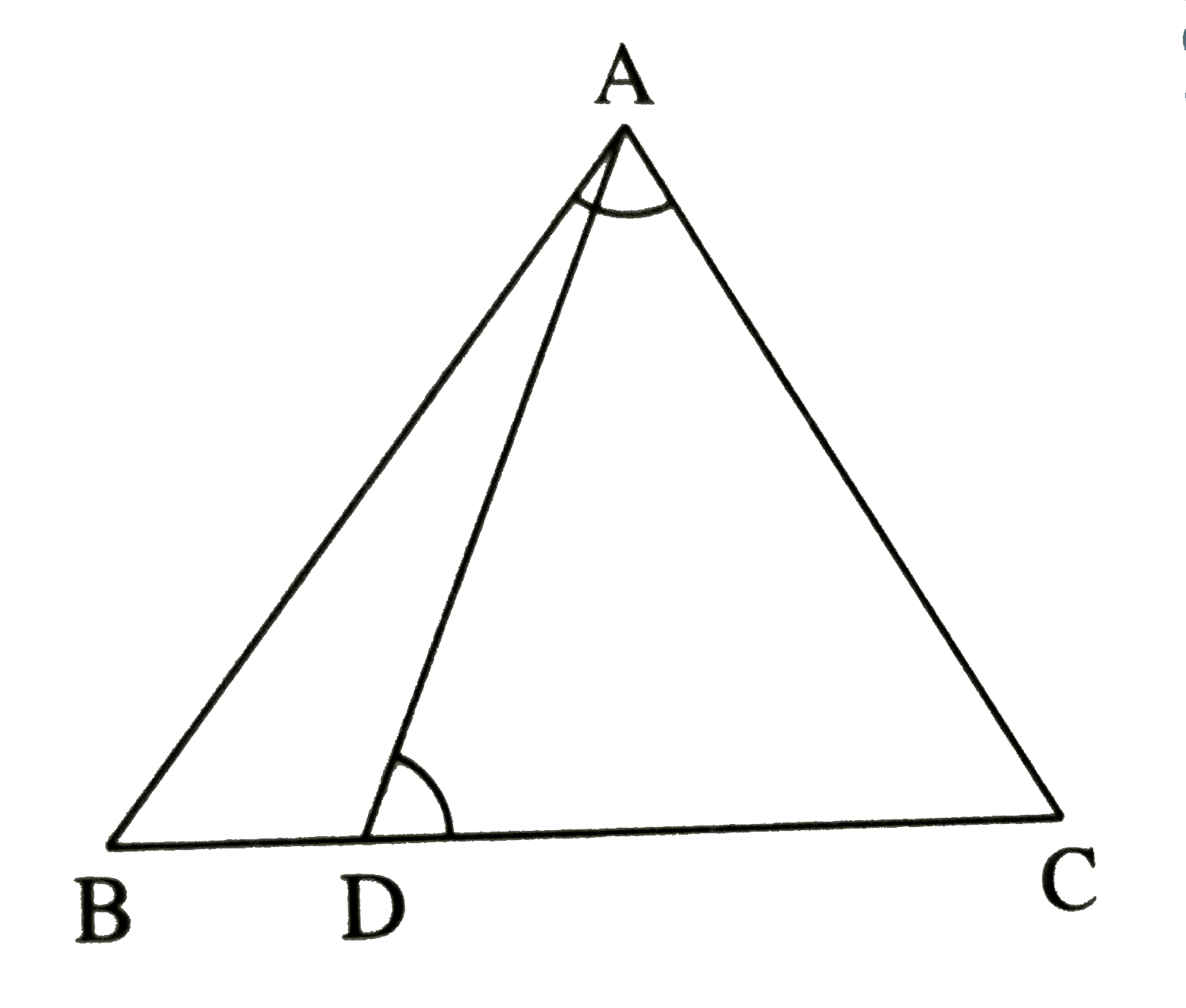 View Solution
View SolutionIn Figure, AD is the median and DEAB. Prove that BE is the median.
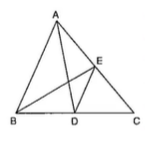 View Solution
View SolutionIn ΔABC,∠A=40∘ and ∠B=60∘ then (2∠A+∠C)=?
View SolutionIn the figure,tangents at B and C of the circle with centre O intersect at point A. If ∠BAC=90∘ then prove □BACO is a square
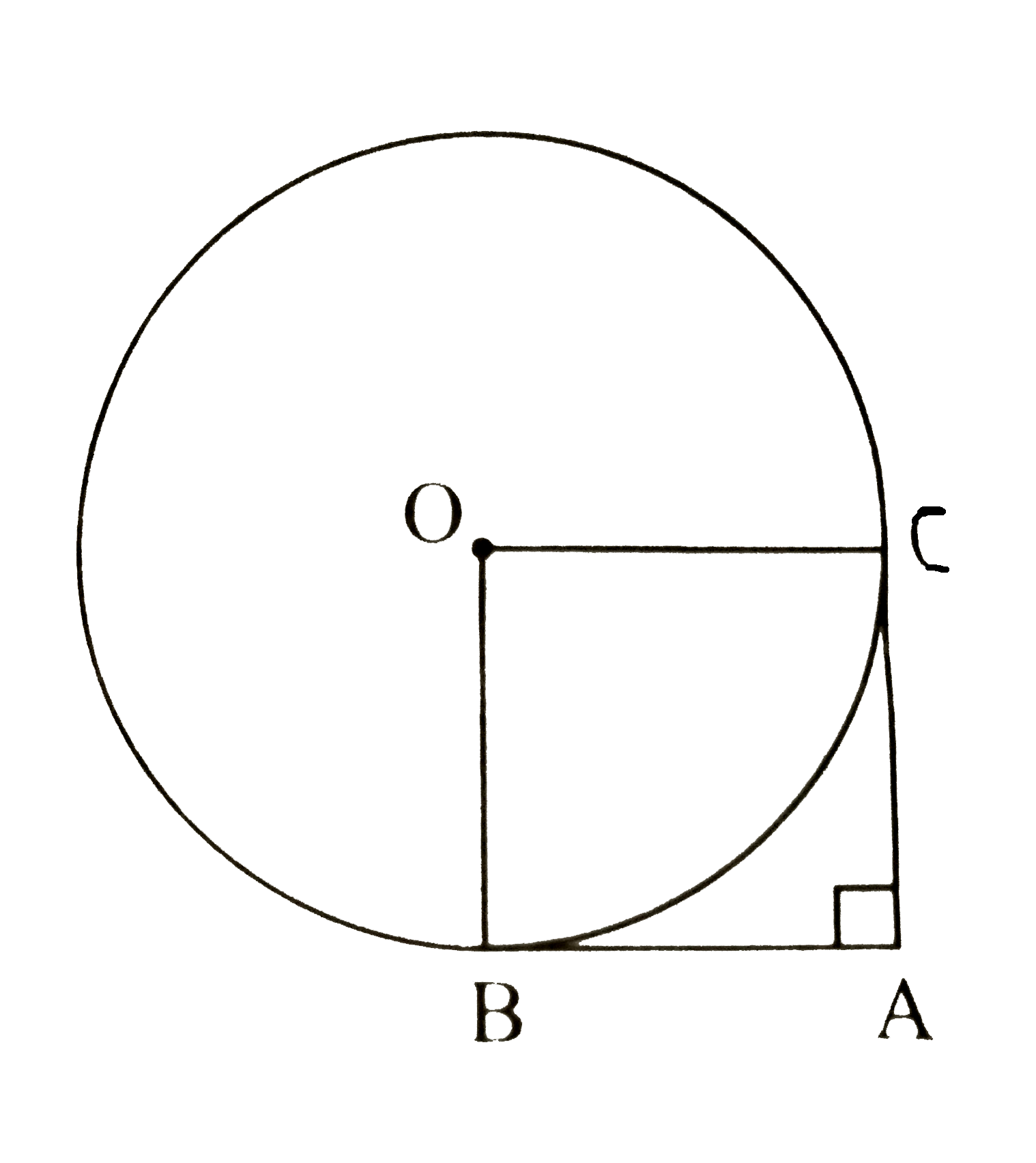 View Solution
View Solution

