In the isosceles ΔABC,AB=AC. The circumcentre of ΔABC is the centre O lies on the opposite side of BC in which a lies. If ΔBOC=100∘, then find the value of ∠ABC∠ABO. Solution in Bengali
In ΔBOC,OB,OC[∴ radii of same circle]
∴∠OBC=∠OCB
or, ∠OBC+∠OBC=∠OCB+∠OBC
or, 2∠OBC=180∘−∠BOCor,2∠OBC=180∘−100∘
or, 2∠OBC=810∘or,∠OBC=80∘2=40∘

Again, the centralangle produced by the are ⌢BC=∠BOC and the angle in cricle =∠BAC.
By theorem -34, ∠BOC=2∠BAC.
or, ∠BAC=12∠BOC=12×100∘=50∘
Now, angleABC=180∘−(∠ACB+∠BAC)
=180∘−∠ABC−50∘[∴∠ACB=∠ABCand∠BAC=50∘]
=130∘−∠ABC
or, 2∠ABC=130∘,or∠ABC=130∘2=65∘
Then ∠ABO=∠ABC−∠OBC=65∘−40∘=25∘
Hence, ∠ABC=65∘and∠ABO=25∘
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)4videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)12videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
03:58View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
03:19View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
04:17View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
03:32View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
04:18View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है । यदि AB2=2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
02:55View SolutionΔABC में, ∠A का समद्विभाजक AD भुजा BC पर लम्ब है। दर्शाइए कि AB = AC है और ΔABC समद्विबाहु है।
 01:35View Solution
01:35View SolutionΔABC में AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
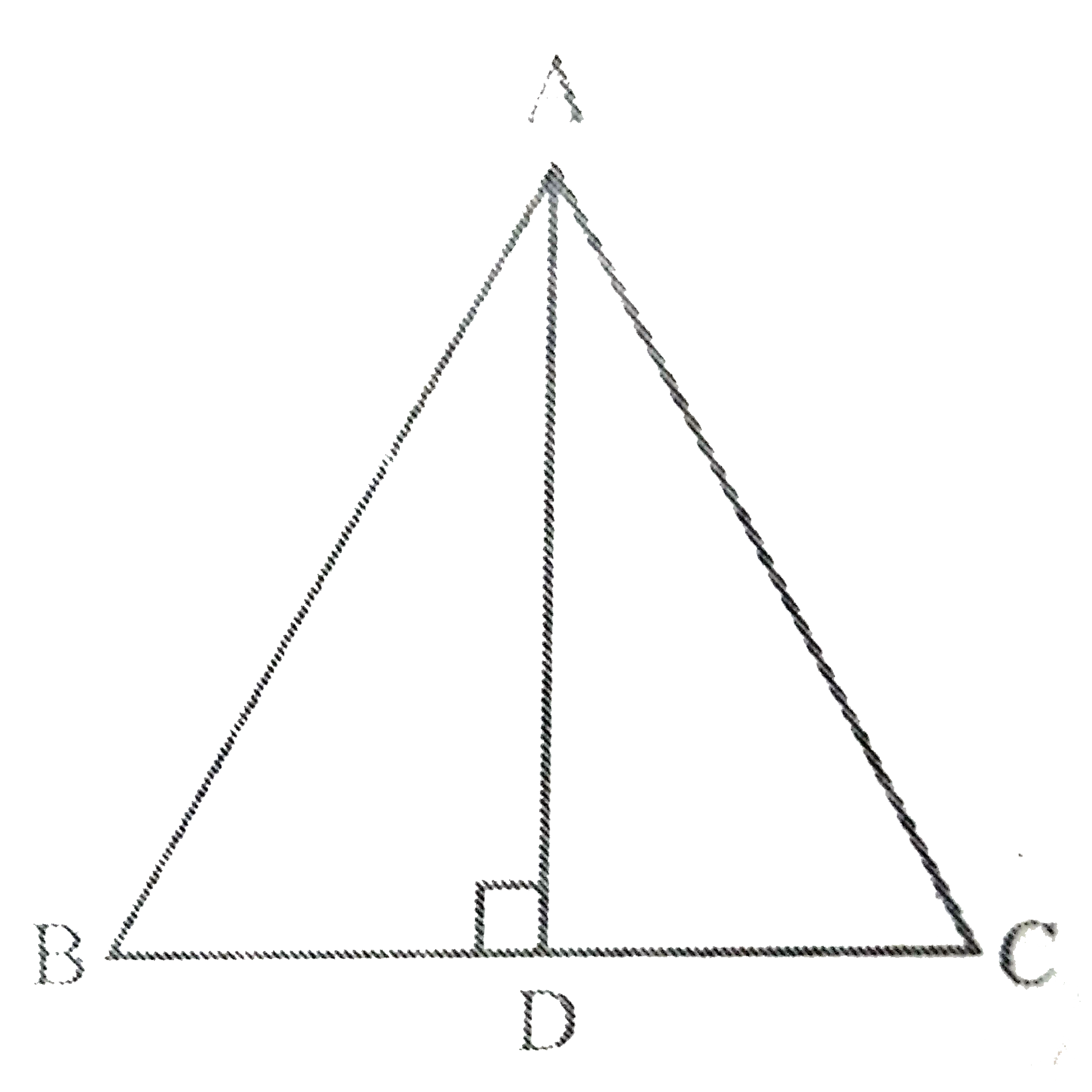 01:44View Solution
01:44View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC =BC है। यदि AB2=2AC2 है , तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
02:10View Solutionआकृति में त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BDCD=ABAC है । सिद्ध कीजिए कि AD , कोण BAC का समद्विभाजन है ।
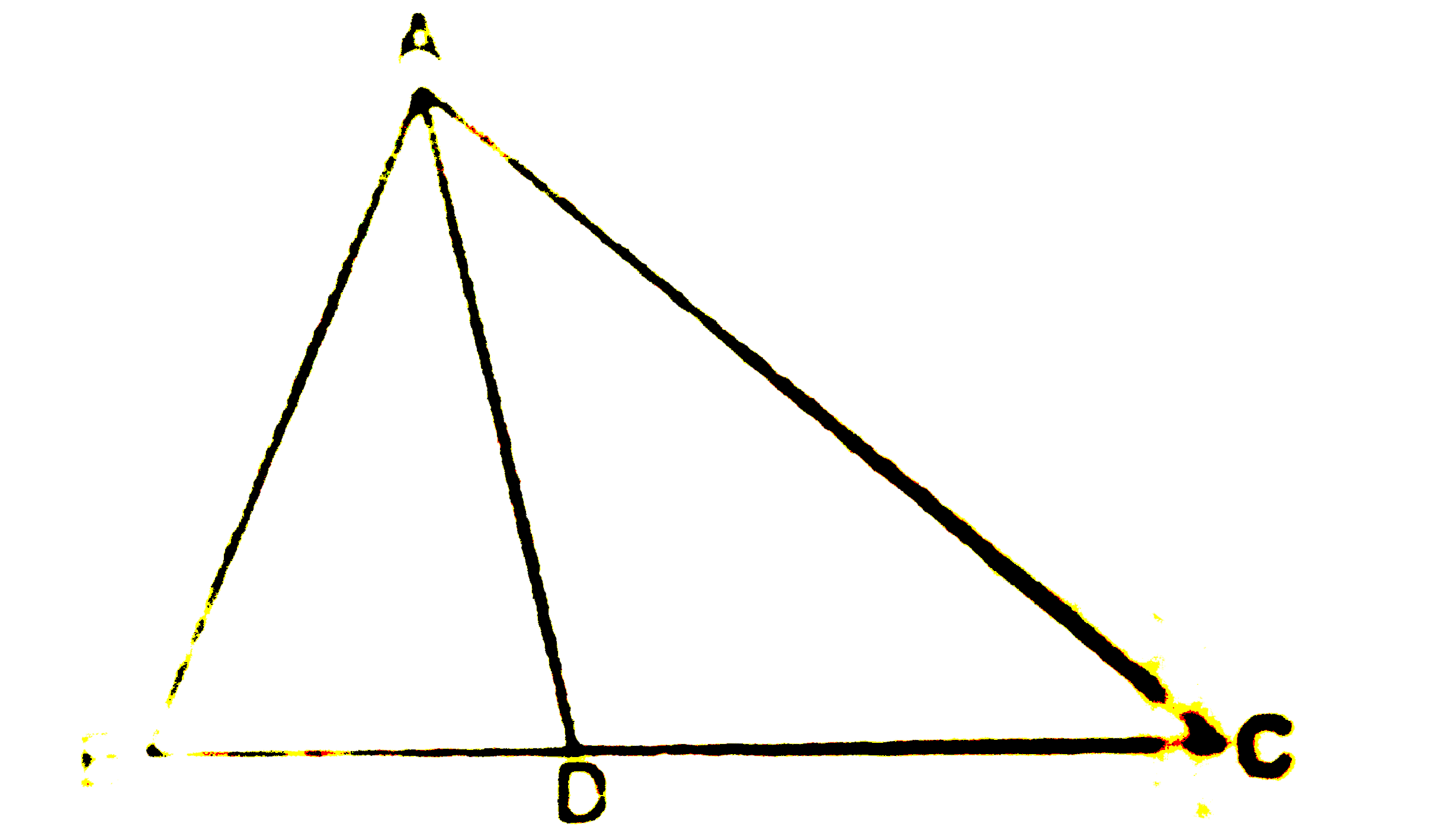 04:55View Solution
04:55View Solution△ABC में ∠A का समद्विभाजक AD भुजा BC पर लम्ब है (आकृति देखिये) दर्शाइए की AB=AC है और △ABC समद्विभाजक है।
01:46View Solutionयदि ABC एक समद्विबाहु त्रिभुज है तथा AC = BC यदि AB2=2AC2 है तो सिद्ध कीजिए कि △ABC एक समकोण त्रिभुज है |
01:49View Solutionएक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AC = BC यदि AB2=2AC2 है तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है |
03:46View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। यदि AB2=2AC2 है, तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
03:00View SolutionABC is an isoscles triangle in which AB =AC. If O be the centre of the circle and ∠OBC=30∘ then the value of ∠ABC is ________
View Solution

