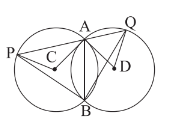
Like the adjoining figure, draw two circles with centres C and D which intersect each other at the points A and B . Draw a straight line through A which intersects the circle C at the point P and the circle with centre D at the point Q. Prove that (i) ∠PBQ=∠CAD(ii)∠BPC=∠BQD. Solution in Bengali
In the circle with centre C,the central angle produced by the chrod AP∠ACP and angle in circle = ∠ABP. By theorem-34,
∠ACP=2∠APBor,∠ABP=12∠ACP......(1)

Again, in the circle which centre at d, the central angle produced by the chord AQ=∠ADQ and angle in circle ∠ABQ.
∴ by theorem-34 ∠ADQ=2∠ABQor,∠ABQ=12∠ADQ.....(2)
then, adding (1) and (2) we get,
∠ABP+∠ABQ=12∠ACP+12∠ADQ
or, ∠PBQ=12∠ACP+∠ADQ
or, ∠PBQ=12(∠ACP+∠ADQ)
=12(180∘−2∠PAC+180∘−2∠QAD)
[∴∠ACP+∠PAC+∠PAC=180∘
or, ∠ACOP+∠PAC+∠PAC=180∘
or,ACP=180∘−2∠PAC
similiarly, ∠ADQ=180∘−2∠QAD]
or, ∠PBQ=12[360∘−2(∠PAC+∠QAD)]=12[360∘−2(180∘−∠CAD)]
=12[360∘−360∘+2∠ACD]=12×∠CAD=∠CAD
∴∠PBQ=∠CAD [ proved (i)]
Now, let us join B,C and B,D
∴CP=CB(∴ radii of same circle), ∴∠BPC=∠PBC......(3)
∴BD=DQ(∴ radii of same circle) ∴∠DBQ=∠DQB.......(4)
Now, from (i) we get,∠PBQ=∠CAD.
or,∠PBC+∠QBA=∠CAB+∠DAB
or,∠PBC+∠CBA+∠DAB
or, ∠PBC+∠CBA+∠DBA−∠DBQ=∠CAB+∠DAB
or, ∠PBC+∠CAB+∠DAB−∠DBQ=∠CAB+∠DAB
[∴CB=CA,∴∠CBA=CAB
∴DB=DA,∴∠DBA=∠DAB]
or, ∠PBC−∠DBQ=0or,∠PBCand∠DBQ=∠BQD]
∴∠BPC=∠BQD [ Proved (ii)]
Hence (i)∠PBQ=∠CADand(ii)∠BPC=∠BQD (Proved)
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)4videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)12videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
04:59View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
03:42View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
05:07View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
07:11View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
04:49View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
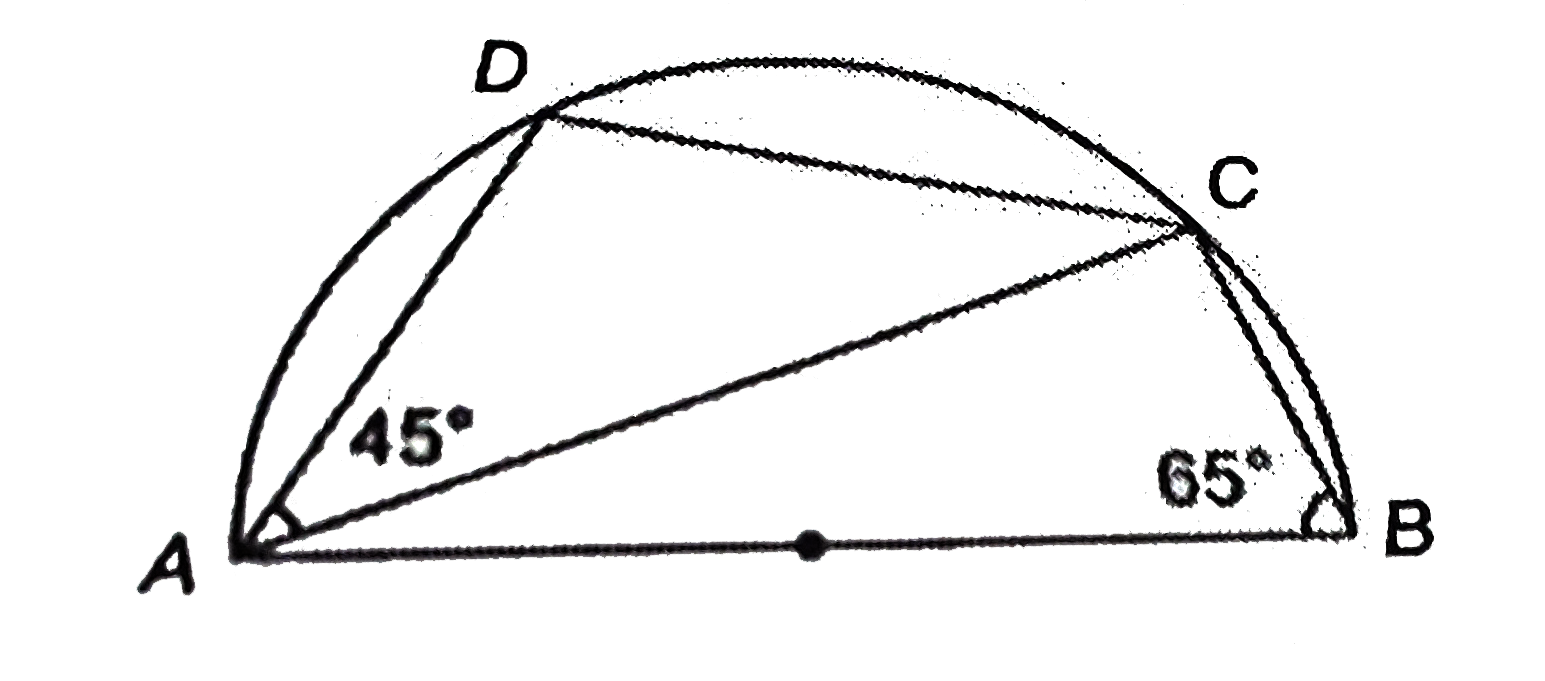
03:14View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
 07:47View Solution
07:47View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
06:44View SolutionTwo circles with centres A and B inrtersect each other at the points C and D. The centre B of the other circle lies on the circle with centre A. if ∠CQD=70∘, then find the value of ∠CPD.
09:02View SolutionAnkita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that ∠AQC=∠BQD.
04:19View SolutionTwo chords AB and CD of the circle with centre at O intersect each other at an internal point P of the centre. Prove that ∠AOD+∠BOC=2∠BPC
07:21View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
05:07View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
04:38View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
06:31View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, ∠PBQ=∠CAD
 04:18View Solution
04:18View Solution

