Two straight lines are drawn through any point X and exterior to a circle to intersect the circle at points A, B and points C, D respectively . Prove that ΔXACandΔXBD are equiangular. Solution in Bengali
ABCD is a cyclic quadrilateral.
∴∠ABD+∠ACD=180∘ …………….(1)
Again , ∠XCA+∠ACD=1straight angle=180∘ ………..(2)
Then , subtracting (1) from (2) we get ∠XCA−∠ABD=0 or ,∠XCA=∠ABD .
Again in cyclic quadrilateral ABDC , ∠BAC+∠BDC=180∘ .........(3)
and ∠XAC+∠BAC=1straight angle=180∘ ........(4) ltbr? Then subtracting (3) and(4) we get,
∠XAC−∠BDC=0 or ,∠XAC=∠BDC
∴ in triangles ΔXACandΔXBD,
∠XCA=∠XBD[∵∠ABD=∠XBD]
and ∠XAC=∠XDB
two angles of each of ΔXACandΔXBD are equal.
Hence ΔXACandΔXBD are equianhular.

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXERCISE-3(Very short - answer type questions)(MCQ)4videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Short -answer type question (S. A.)2videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXAMPLE (Short - answer type questions)5videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )9videos
THEOREMS RELATED TO CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
Similar Questions
If the length of diagonal of a square is √72cm, then calculate the area of the square.
02:18View SolutionIf the length of diagonal of a square is 12√2m, then calculate the area of the square.
04:59View SolutionIn the adjoining figure , if ∠BAD=60∘.∠ABC=80∘ , then find the values of ∠DPCand∠BQC .
05:07View SolutionProve that diameter is the greatest chord of a circle.
04:49View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
07:47View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
09:27View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
03:35View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
19:41View SolutionAnkita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that ∠AQC=∠BQD.
04:19View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
07:21View SolutionTwo circles intersect each other at the points G and H . A straight line is drawn through the point G which intersect two circles at the points P and Q and the straight line through the point H parallel to PQ intersects the two circles at the points R and S . Prove that PQ=RS .
08:51View SolutionTwo circle intersect at two points B and C. Through B, Two lines segment ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ACP=QCD.
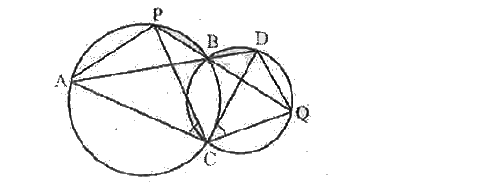 04:30View Solution
04:30View Solutionகொடுக்கப்பட்ட படத்தில் O மையமாக உடைய வட்டத்தின் ஆரம் 5 செ .மீ ஆகும் .T ஆனது OT =13 செ .மீ என அமைந்த ஒரு புள்ளி மற்றும் OT ஆனது வட்டத்தை E ல் வெட்டுகிறது,வட்டத்தின் E என்ற புள்ளியின் வழியாக செல்லும் ஒரு தொடுகோடு AB எனில் ,AB -யின் நீளம் காண்க ?
04:32View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, ∠PBQ=∠CAD
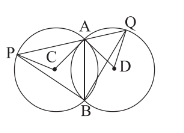 04:49View Solution
04:49View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, ∠BPC=∠BQD
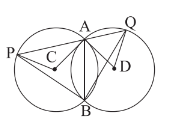 06:31View Solution
06:31View Solution

