ABCD is a cyclic quarilateral. The bisectors of ∠aand∠C in tersect the circle at the points E and F respectively . Prove that EF is a diameter of the circle. Solution in Bengali
Let ABCD is a cyclic quadrilateral in the circle with centre at O . The bisector AE of the ∠A intersects the circle at E and the bisector of the ∠C intersects the circle at F .Let us join E F
To Prove : EF is a diameter of the circle.
Construction : Let us join C, E.
Proof : ABCD is a cyclic quadrilateral.
∴∠BAD+∠BCD=180∘
or. 12∠BAD+12∠BCD=90∘ [dividing by 2 ]
or, ∠DAE+∠DCF=90∘ [∵ BE and CF are the bisectors of ∠Aand∠C respectively]
But two angles in circle produced by the arc DE are ∠DAEand∠DCE.
∴ ∠DAE=∠DCE
∴ from (1) we get , ∠DCE+∠DCF=90∘ or ∠ECF=90∘
∴ ∠ECF is semicircular angle.
Hence EF is a diameter of the circle .

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXERCISE-3(Very short - answer type questions)(MCQ)
4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Short -answer type question (S. A.)
2 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXAMPLE (Short - answer type questions)
5 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )
9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
Similar Questions
If the length of diagonal of a square is √72cm, then calculate the area of the square.
View SolutionIf the length of diagonal of a square is 12√2m, then calculate the area of the square.
View SolutionIn the adjoining figure , if ∠BAD=60∘.∠ABC=80∘ , then find the values of ∠DPCand∠BQC .
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf the bisectors of the opposite angle ∠Pand∠R of a Cyclic quadrilateral PQRS intersect the corresponding circle at A and B respectively; then AB is a diameter of the circle.
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
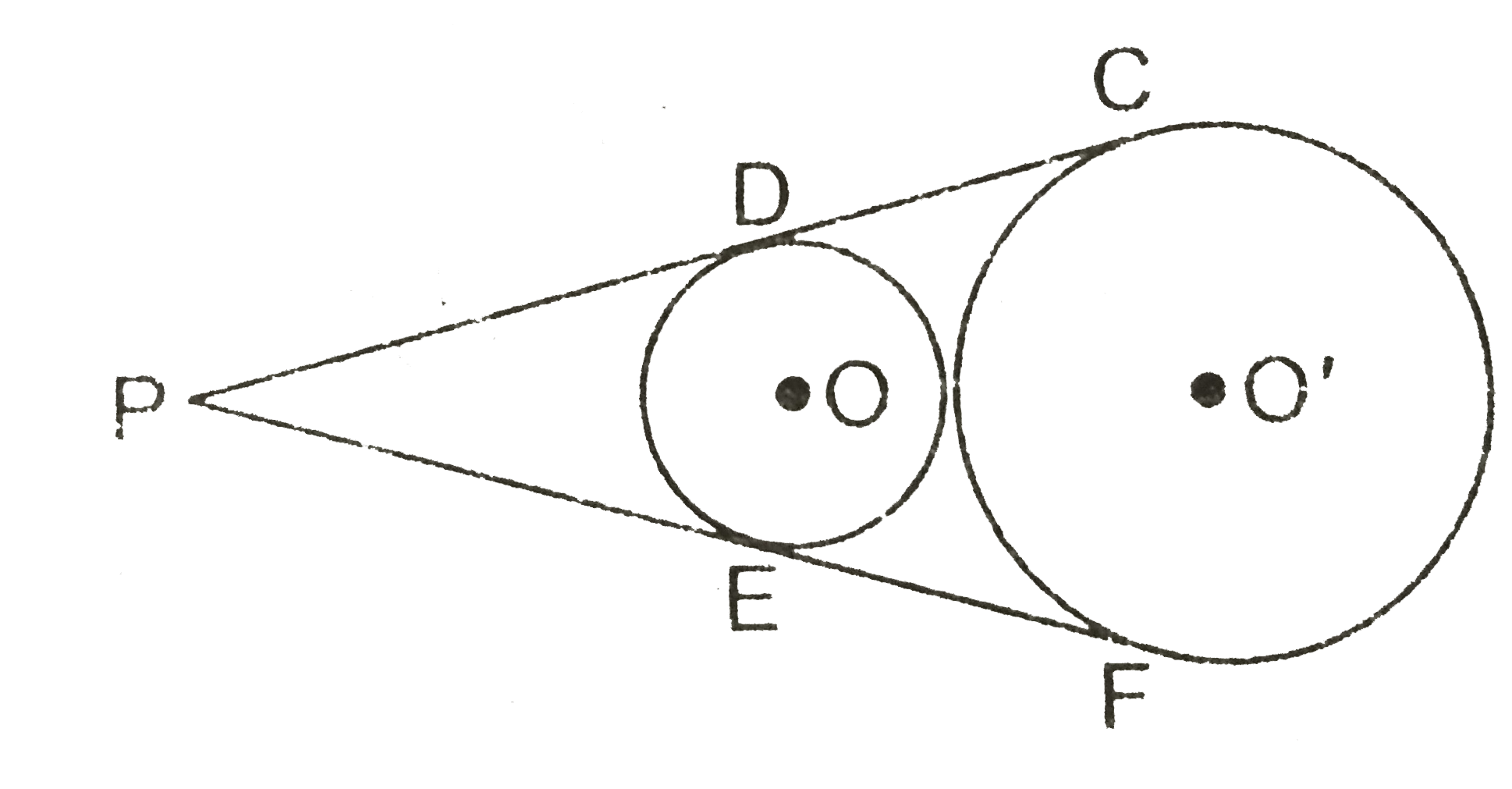
View Solutionदिये गये चित्र में, बाह्रा स्पर्श करने वाले दो वृत्तों कि उभयनिष्ठ अनुस्पर्शी रेखाएँ PDC तथा PEF खींची गयी हैं जो वृत्तों को क्रमशः D व C तथा E व F पर स्पर्श करती हैं। सिद्ध कीजिए - DC = EF
(अथवा) चित्र में, दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ PDC और PFE हैं। सिद्ध कीजिए कि CD = EF
(अथवा) चित्र में, दो वृत जिनके केन्द्र O और O हैं, बाह्यतः स्पर्श करते हैं। इन वृत्तों कि दो उभयनिष्ठ अनुस्पर्शी रेखाएँ PDC तथा PEF खींची गयी हैं जो वृत्तों को क्रमशः D व C तथा E व F बिन्दुओं पर स्पर्श करती हैं। सिद्ध कीजिए कि DC = EF
View SolutionABCD is a cyclic quadrilateral. The side BC of it is extended to E . Prove that the two bisectors of ∠BADand∠DCE meet on the circumferncee of the circle .
View SolutionIn a cyclic quadrilateral ABCD, the bisectors of opposite angles A and C meet the circle at Pand Q respectively. Prove that PQ is a diameter of the circle.
View Solutionयदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q बिन्दुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
View Solutionआकृति में, ABCD एक चक्रीय चतुर्भुज है| एक वृत्त जो A और B से होकर जाता है, AD और BC को बिंदुओं E और F पर मिलता है | सिद्ध कीजिए कि EF∣∣DC है|

View SolutionAngles opposite a cyclic quadrilateral ABCD angleA And angleC Let's intersect the bisector circle at the point E and F respectively. Prove that EF will be the diameter of the circle.
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View Solution
