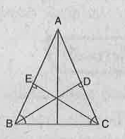
BE and CF are perpendicular on sides AC and AB of triangles ABC respectively . Prove that four points B , C ,E , F are concyclic. Also prove that the two angles of each of ΔAEFandΔABC are equal. Solution in Bengali
BE⊥AC,∴∠BEC=90∘
Also CF⊥AB,∴∠sBFC=90∘ , i.e , at two points E and F the same side of BC , the produced angles are equal are equal.
∴ B ,C ,E ,F, are concyclic.
Now , in ΔAEF,∠AEF=∠AEB−∠BEF
90∘=∠BEF[∵∠AEB=90∘]
= 90∘−∠BCF[∵∠BCF=∠BCF same angles in circle produced by the arc BF] ltbr =90∘−∠BCF[∵BEF=∠BCF same angles in circle produced by the BF]
=∠CBF[∵∠BFC=90∘]
Again , ∠AFE=∠AFC=∠CFE=90∘−∠CFE [∵∠AFC=90∘]
=90∘−∠CBE[∵∠CFE=∠CBE , same angle in circle produced by the arc CE ]
=∠BCE [∵∠BEC=90∘]
∴inΔ'sAEFandΔABC,∠AEF=∠ABC [∵∠CBF=∠ABC]
and ∠AFE=∠ACB [∵∠BCE=∠ACB]
Hence two angles of each of ΔAEFandΔACB are equal.

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXERCISE-3(Very short - answer type questions)(MCQ)
4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Short -answer type question (S. A.)
2 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXAMPLE (Short - answer type questions)
5 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )
9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
Similar Questions
If the length of diagonal of a square is √72cm, then calculate the area of the square.
View SolutionIf the length of diagonal of a square is 12√2m, then calculate the area of the square.
View SolutionIn the adjoining figure , if ∠BAD=60∘.∠ABC=80∘ , then find the values of ∠DPCand∠BQC .
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionABC is a triangle is which BE and CF are, respectively, the perpendiculars to the sides AC and AB . If BE=CF , prove that ABC is isosceles.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionIf BM and CN are the perpendiculars drawn on the sides AC and BC of the ΔABC, prove that the points B, C, M and N are concyclic.
View Solutionएक न्यूनकोण त्रिभुज ABC है । B से AC पर लम्ब ,C से AB पर लम्ब के बराबर है तो सिद्ध कीजिए कि AB = AC
View SolutionIn ΔABC,AB=AC,BEandCF are resepectively the bisectors of ∠ABCand∠ACB and itersect the sides AC and AB at the points E and F resepectively. Then four points B,C,E,F are not concylic.
View SolutionIn ΔABC , AB =AC , BE and CF are the bisectors of the angles ∠ABCand∠ACB and they intersect AC and AB at the points E and F respectively. Then four points B ,C ,E , F are not concyclic.
View Solutionएक त्रिभुज ABC में BE तथा CF क्रमशः भुजाओं AC तथा AB पर डाले गए लम्ब हैं | यदि BE=CF हो, तो सिध्द करो कि ΔABCसमद्विबाहु है |
View SolutionABC एक त्रिभुज है जिसमें B और C शीर्षों के सम्मुख भुजाओं पर BE और CF लंब डाले गए हैं । सिद्ध करें कि B,C,E,F एकवृत्तीय है।
View SolutionΔABC ఒక సమద్విబహు త్రిభుజము. సమాన భుజాలు AC,AB లకు గీసిన లంబాలు వరుసగా BE మరియు CF అయిన ఈ లంబాలు సమానమని చూపండి.
View Solutionসত্য বা মিথ্যা লেখো : ABC ত্রিভুজের AB=AC, BE ও CF যথাক্রমে ∠ABCও ∠ACB -এর সমদ্বিখণ্ডক এবং AC ও AB যথাক্রমে E ও F বিন্দুতে ছেদ করে । B, C, E, F বিন্দু চারটি সমবৃত্তস্থ নয় ।
View Solution
