The resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
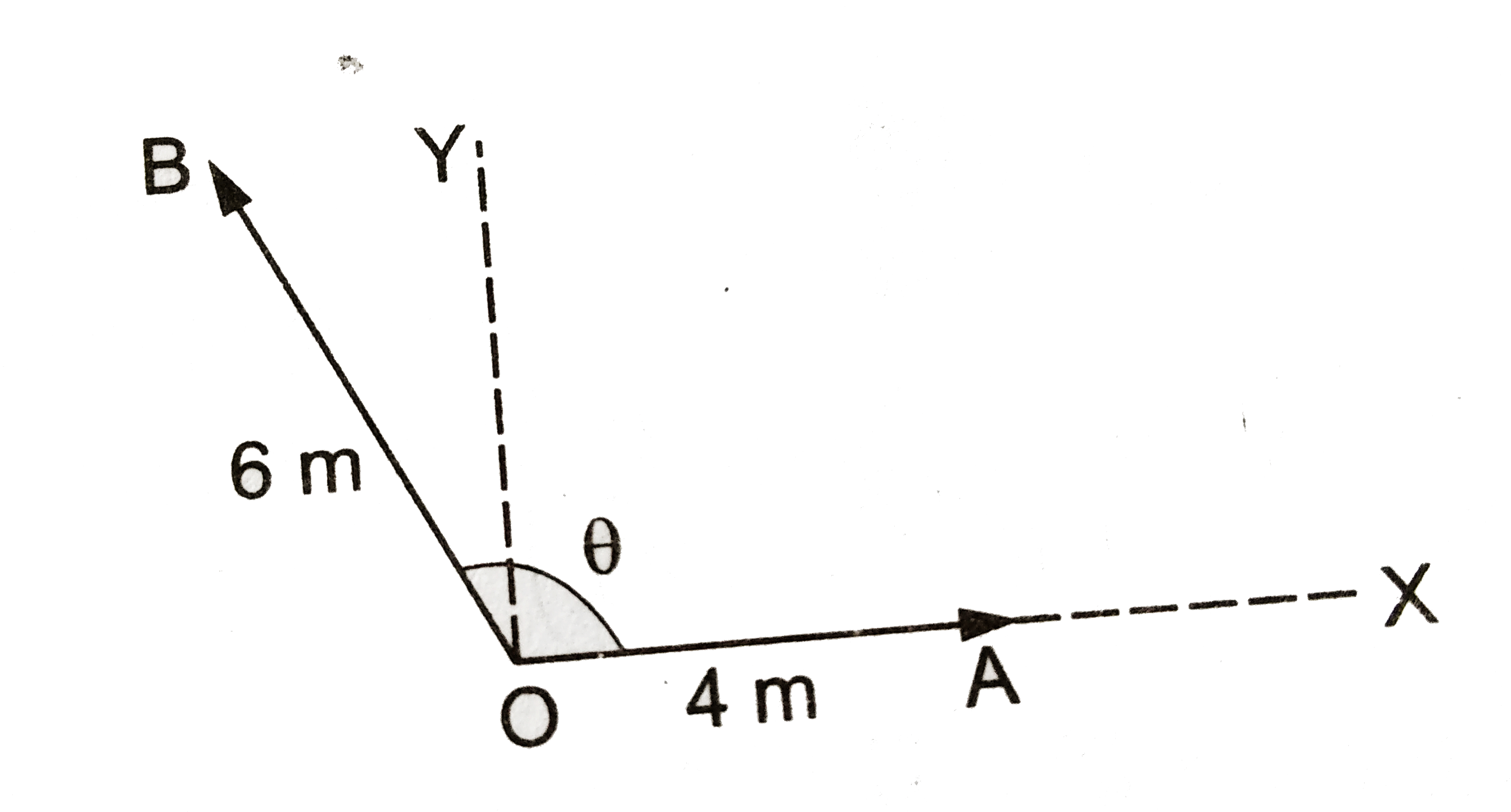
Take the dotted lines as X,Y axes.
x -component of −−→OA=4m,x−compo≠ntof<br>vec(OB)=6 m costheta.<br>x−compo≠ntoftherestant–––––=(4+6cos theta)m.<br>Butitisgiventˆtherestant–––––isalongY−aξs.Thus,the−compo≠ntoftherestant–––––=0<br>4+6cos theta = 0, or, costheta = 2/3
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 1
6 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
Similar Questions
The resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View SolutionThe resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View Solution
Knowledge Check
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of theseThe resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
A30∘B45∘C150∘D120∘The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
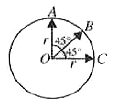 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1)
The magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionFind the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View SolutionMagnitude of resultant of two vector →A and →B is equal to 2. angle between two vectors is 180∘ if ∣∣→A∣∣=3 then find ∣∣→B∣∣
View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View Solution
