A block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system.

The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle θ with horizontal. Find the acceleration of m and M after release.
Method 1: Just after the release of system, block M will move towards left (say with acceleration A) and block m will move down with respect ot M (say with acceleration a). As there is no motion of M is vertical direction, hence the acceleration of m in verticle direction will be same as that of M, i.e. A, because horizontal both move together.
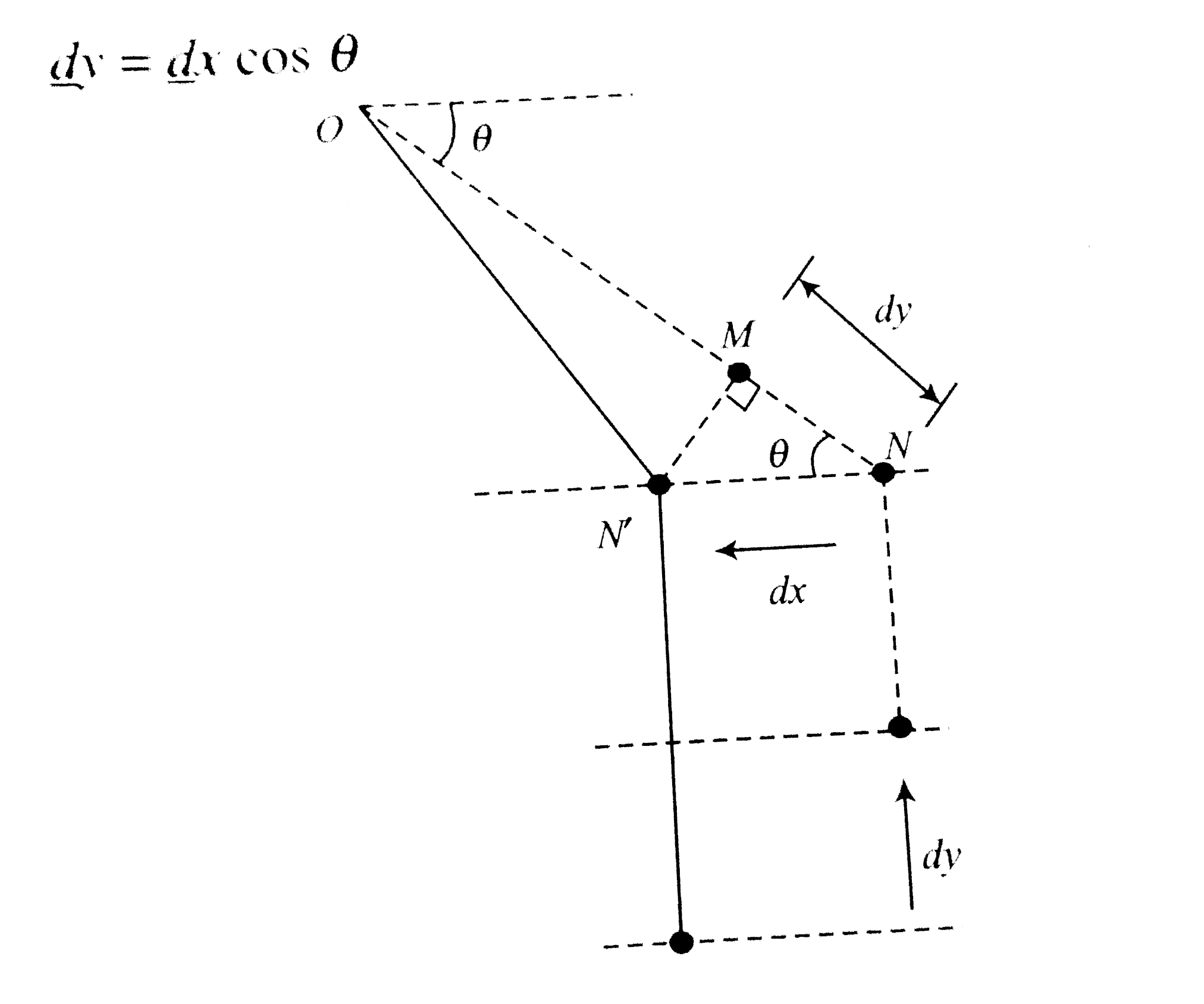
Finding constraint Method 1: Let just after release, during a small time dt, the displacement of m(w.r.t. M) is dy downwards and that of M is dx horizontally as shown in fig.
Decreases in the length of segment I=d¯xcosθ
Increases in the length of segment II' d¯y
As the total length of the string is constant , so
d¯=d¯xcosθ ..(i)
Divinding both sides by dt, we get
dydt=dxdtcosθ⇒v=Vcosθ ..(ii)
differenting w.r.t. t=dvdt=V(−sinθ)dθdt+dVdtcosθ
But initially V=0, as a=Acosθ ...(iii)
(∴dvdt=a,dVdt=A)
Method 2: we can obtain (i) in the following way.
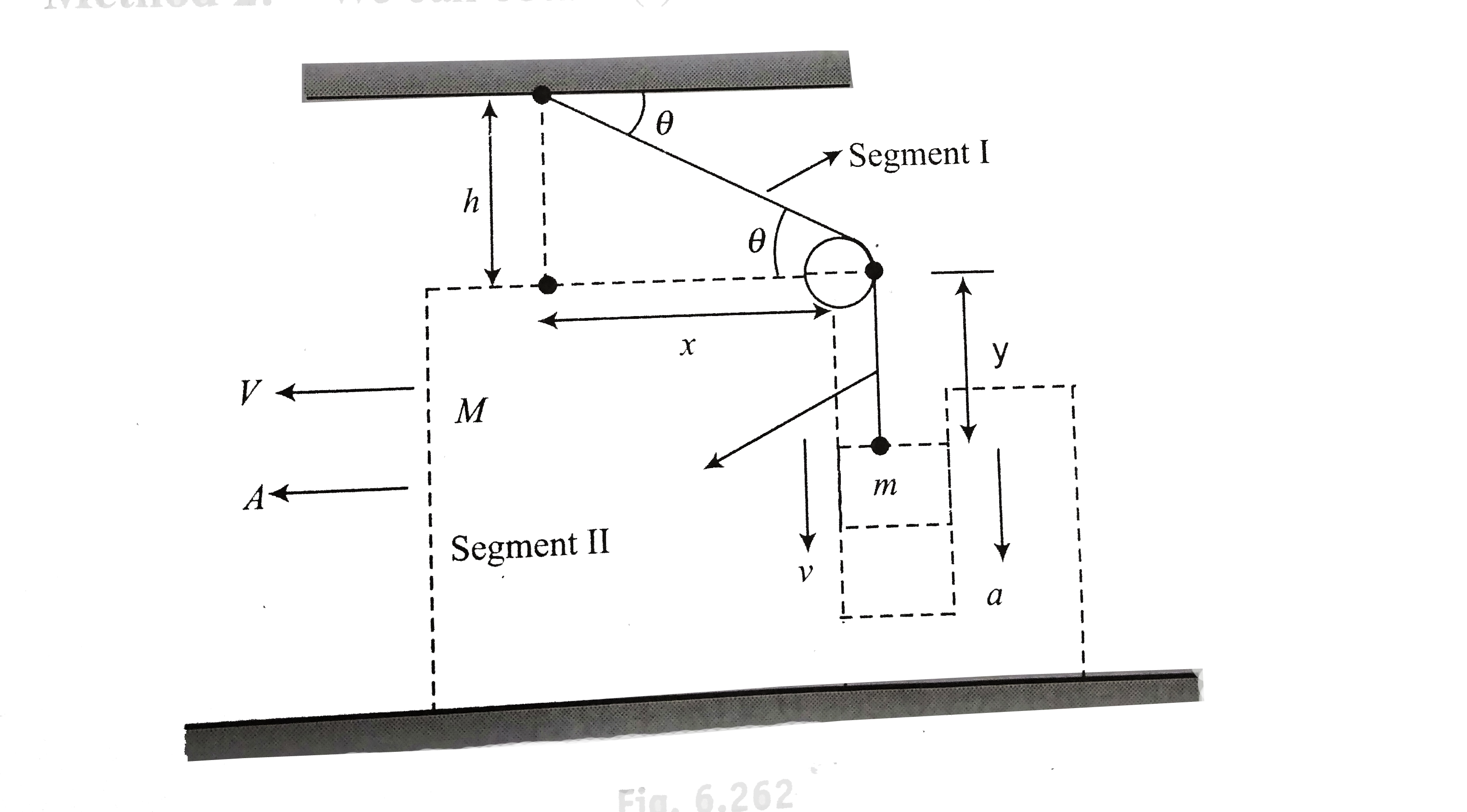
The displacment of M towards left is dx, then its component along AP is dxcosθ should be decreased in the length of segment I and this should be equal to increases in the length of segment II which is dy. Hence, dy=dxcosθ.
⇒a=Acosθ
Method 3:
Total length of string : l=√h2+y2+x
differentiating w.r.t. t=dldt=d(h2+x2)1/2dt+dxdt
⇒0=2ydydt2√h2+y2+dxdt⇒0=cosθ(−V)+r
(∵dxdt=v,dydt=−V (as y decreases with time)
and cosθ=y√h2+y2
⇒v=Vcosθ which is same as (ii)
Now finding acceleration of blocks
We can use any of the following method to find the value of A and a .

Method 1: From FBD of M:
Tcosθ−N=MA ...(iv)
From FBD of m: N=mA ..(v)
mg−t=ma ..(vi)
Combining (iv) and (v) we get
Tcosθ=(m+M)A ...(vii)
Putting a=Acosθ in (iv) we get
mg−T=mAcosθ ..(viii)
Put the value of T form (viii) into (vii) we get
(mg−mAcosθ)cosθ=(m+M)A
⇒A=mgcosθM+m(1+cos2θ)
and a=Acosθ=mgcos2θM+m(1+cos2θ)
The net acceleration of m is
√A2+a2=A√1+cos2θ=mgcosθ√1+cos2θM+m(1+cos2θ)
Method 2: Analyzing the block with w.r.t. wedge

W.r.t M, m has only vertcal acceleration which is a downwards. Here we have to apply pseudo force because M is a non inertial frame.
FBD of m w.r.t. M:
N=mA,mg−T=ma
These equation are same as (v) and (vi). Now solve to get answer.
Method 3: Analyzing the block and wedge together
Analyzing the system of (M+m), i.e. , block and wedge together in horizontal direction, in horizontal direction both masses have same acceleration which is A.
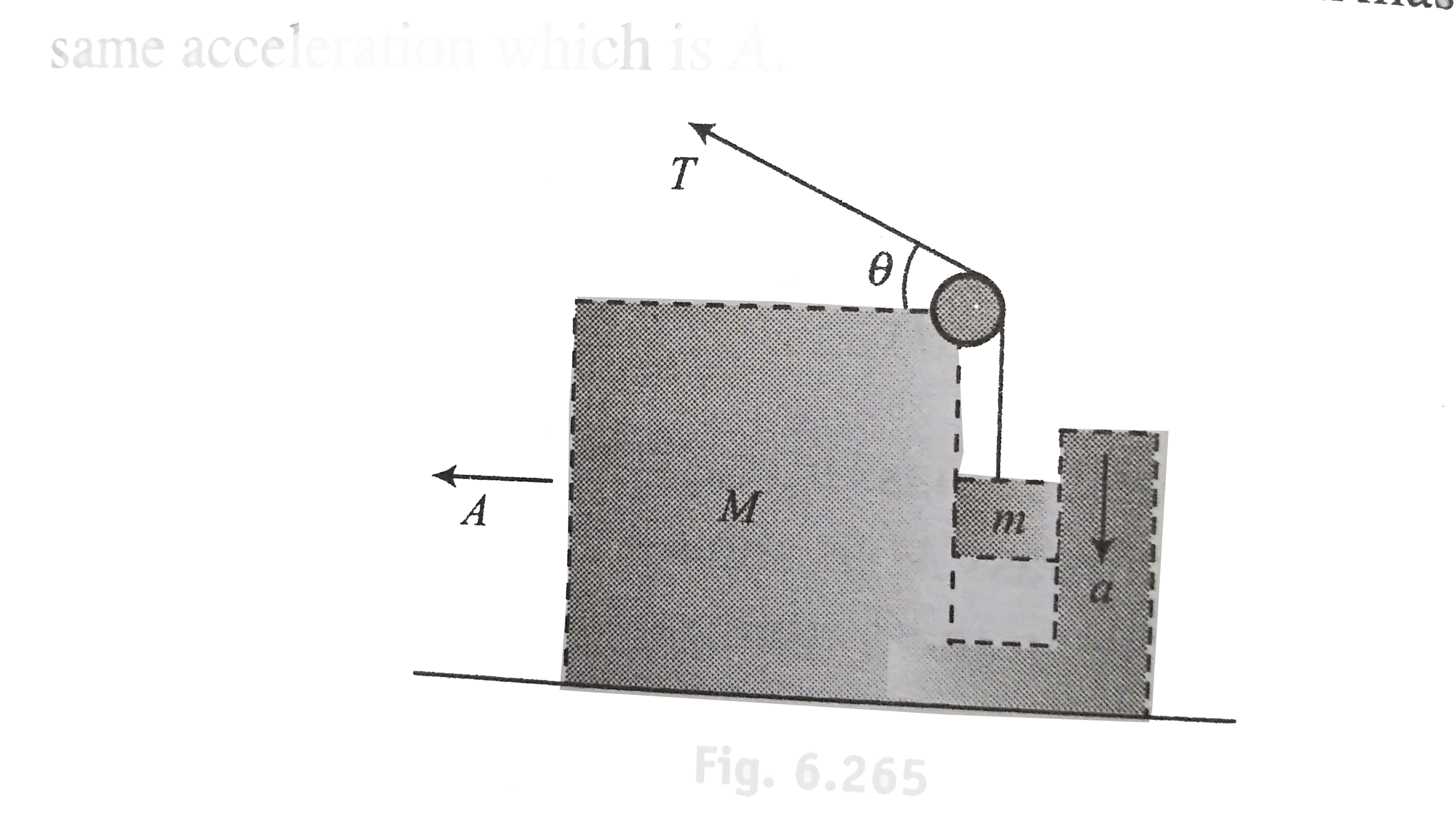
Tcosθ=(M+m)A ...(ix)
Analyzing the motion of blcok in vertical direction
mg−T=ma ..(x)

Solving (ix) and (x) , we get
A=mgcosθM+m(1+cos2θ)
and a=mgcos2θM+m(1+cos2θ)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A block of mass m can slide freely along the verticle surface of a bigger block of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end is fixed at point P.
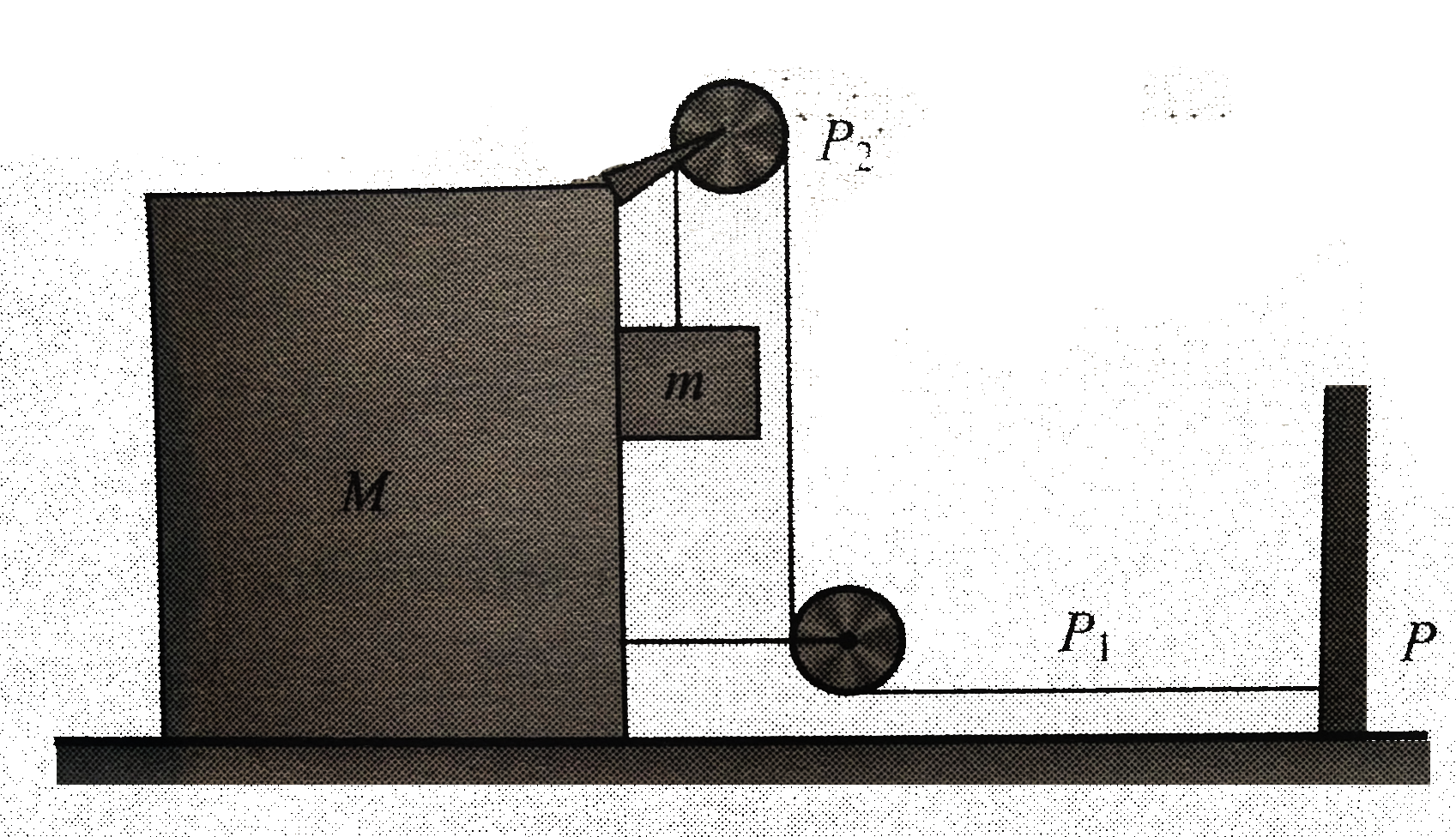
The string between P1 and P is horizontal and other parts of the string are vertical. system is released from rest. Find the acceleration of m and M during their subsequent motion.
View SolutionA block of mass m can slide freely along the verticle surface of a bigger block of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end is fixed at point P.
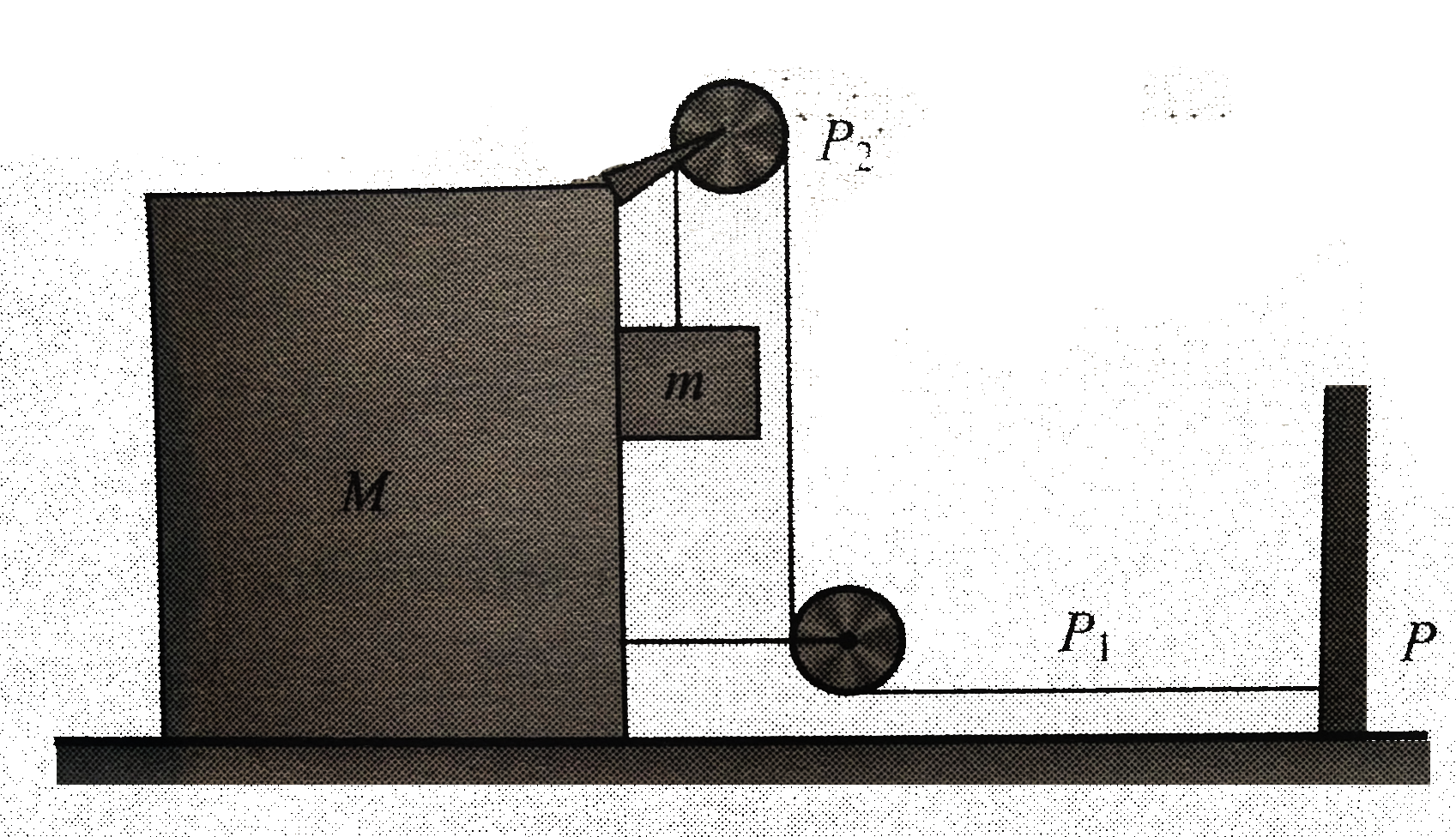
The string between P1 and P is horizontal and other parts of the string are vertical. system is released from rest. Find the acceleration of m and M during their subsequent motion.
View Solution
Knowledge Check
A thin uniformed rod of mass m and length L is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass 2m) and a block of mass 2m is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of 37∘ with horizontal. Based on above information answer the following question :
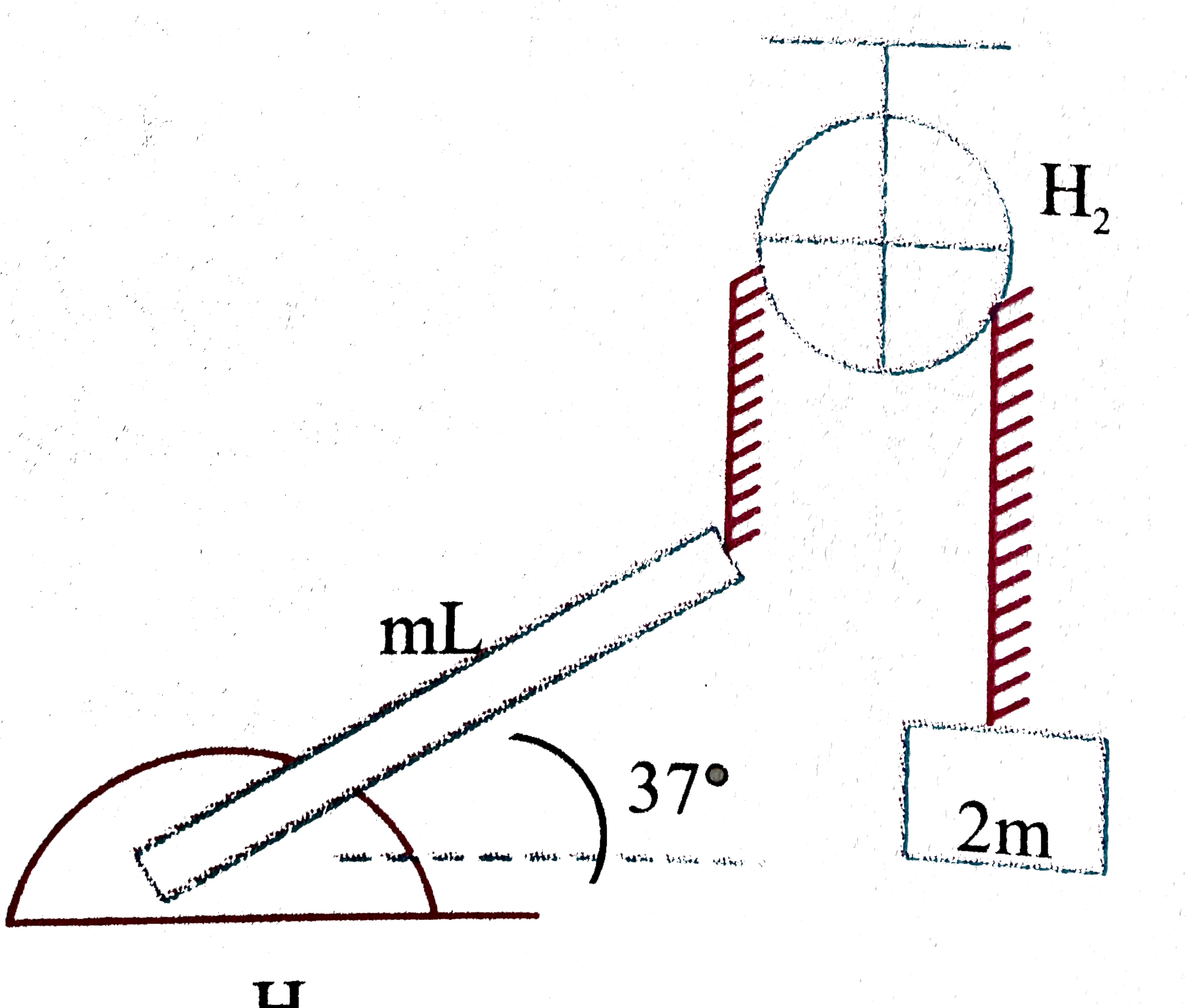
Just after releases of the system from rest acceleration of block isA72g121, downwardsB48g119, downwardsC90g121, downwardsD90g121,upwards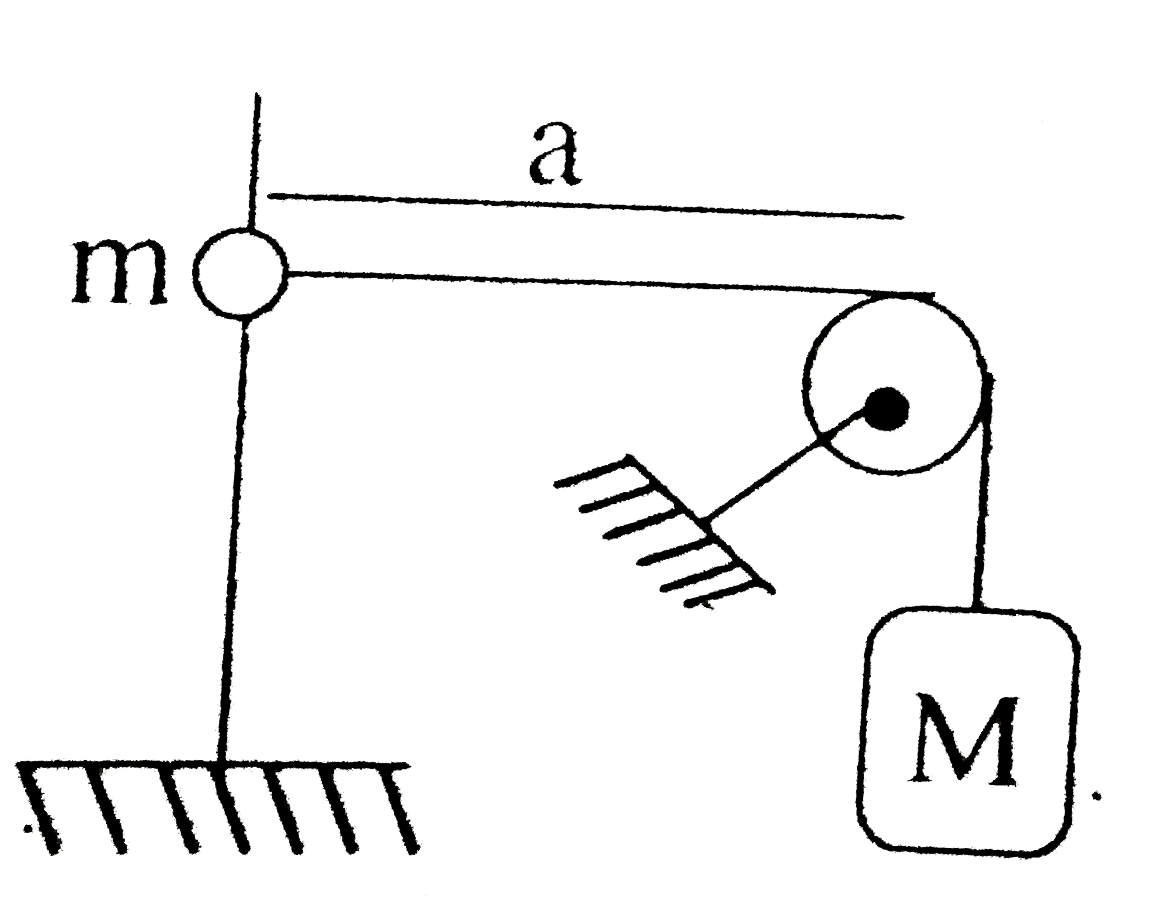
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string isAT=MgBT>MgCT<MgDT=Mg+Mg
A ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
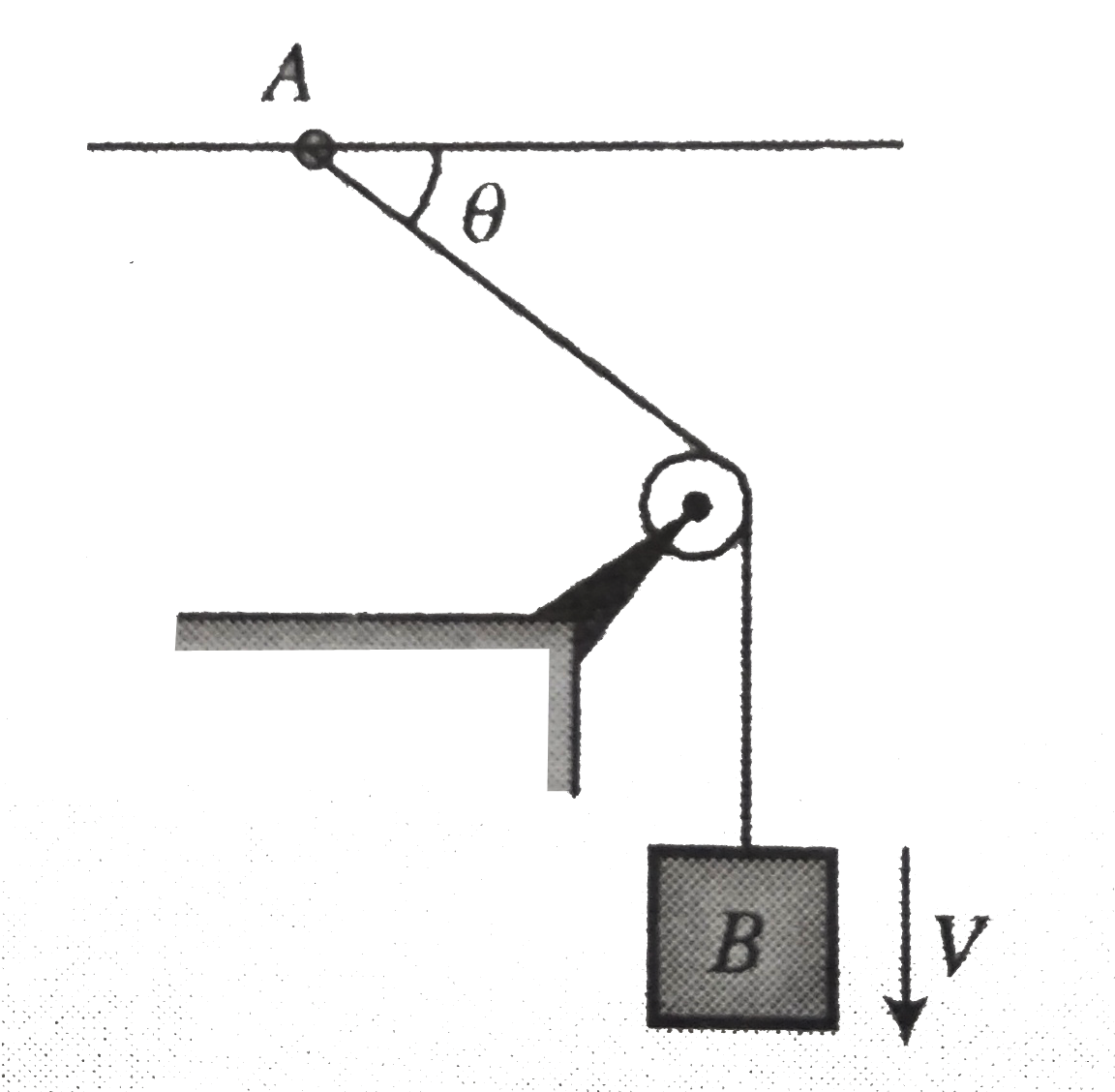
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.

View SolutionA block of mass M si suspended by two strings angles θ1 and θ2 with the horizontal. Find the tensions in the strings.

View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
View Solution
