A block of mass m can slide freely along the verticle surface of a bigger block of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end is fixed at point P.
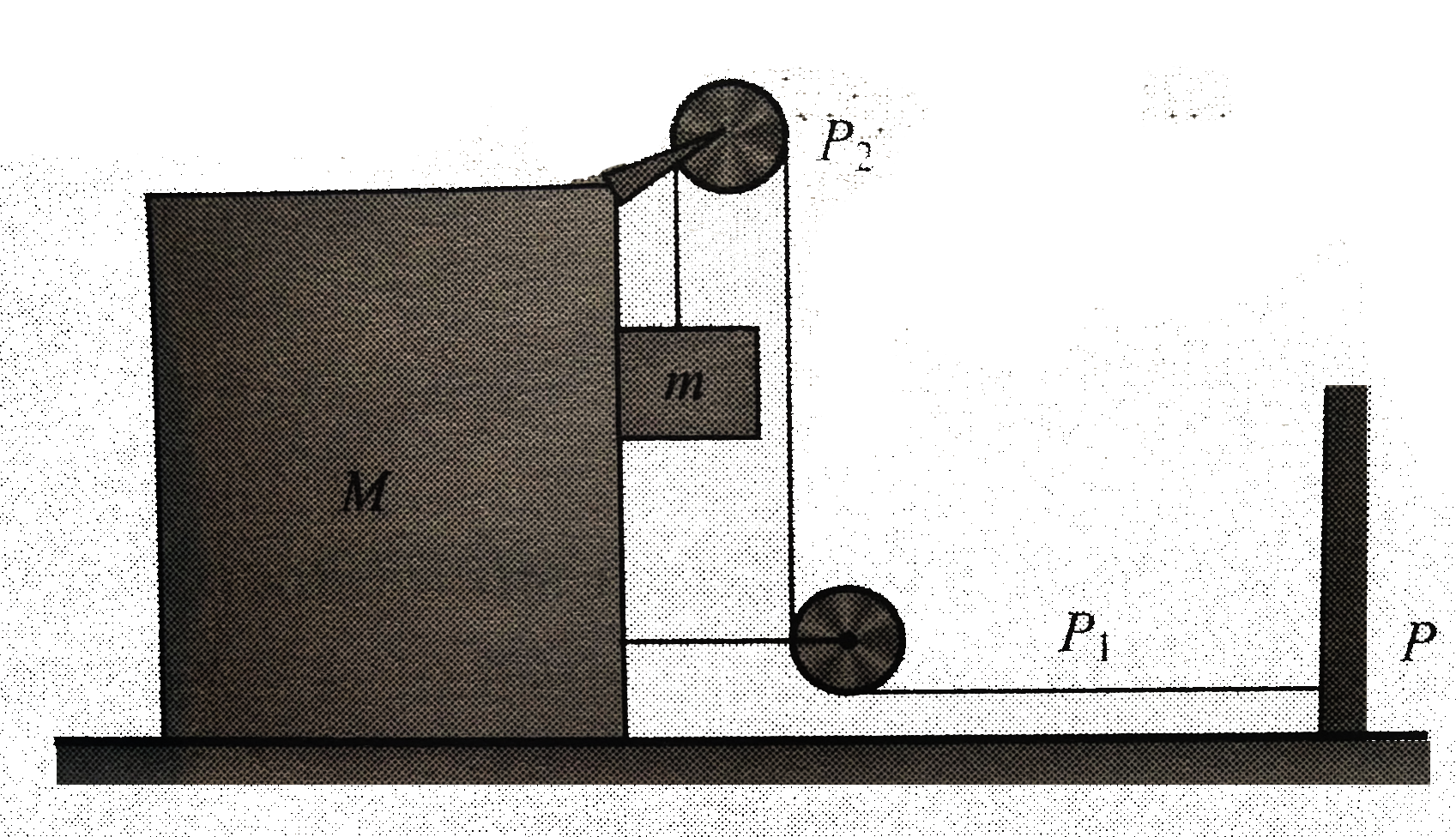
The string between P1 and P is horizontal and other parts of the string are vertical. system is released from rest. Find the acceleration of m and M during their subsequent motion.
Let us divde the string in three segments as shown in fig. As we release the system, the block m will try to move downwards due to which the length of segment I will increses. Then the length of segment III should decreses because the length of segment II is fixed. This will make M to move toward right. Let the acceleration of m downward be a and the acceleration of M toward right be A. Then in horizontal direction, the acceleration of m will also be A, because m is constrained to move horizontally with M.

Constraint relation: As the length of string is constant, there should not be any change in the length of string although there can be change in the individual segments of string. Let during some time, m moves downwards a distance x and M moves towards right a distance X.
Change in the length of segment I=+x
Change in the length of segment II=0
Change in the length of segment III = -X
But net change is zero, so (+x)+0+(−X)=0⇒x=X
Differentiating twice w.r.t. time, we get a=A (i)
Now finding the accelerations.
Method1 !: Analyses from ground frame:
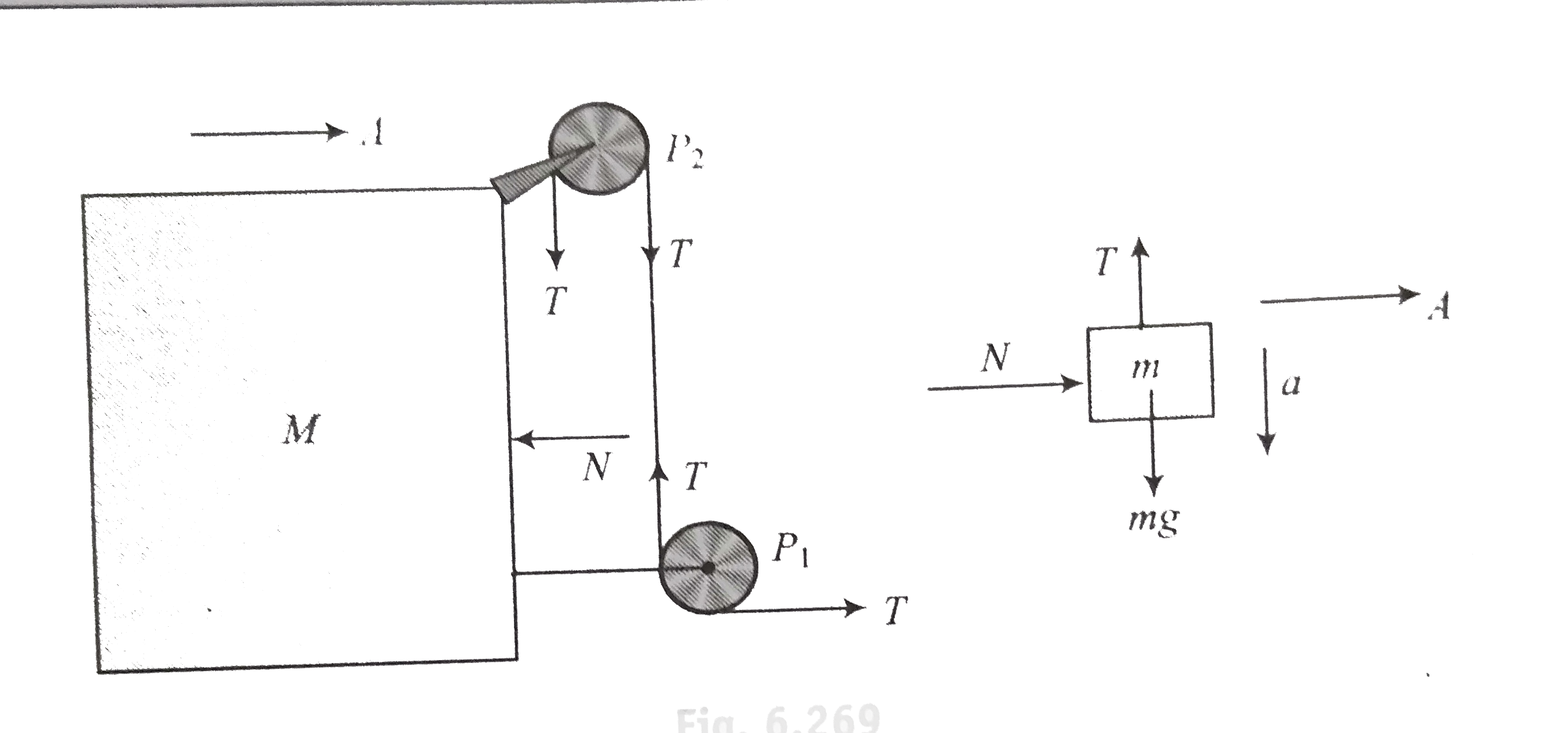
If we make FBDs of M and m separately, then
From FBD of M:
T−N=MA...(ii)
Form FBD of m:
N=mA
and mg−T=ma ...(iv)
From (ii) and (iii), we get
T=(M+m)A...(v)
Equation (v) is same is (ii). Now solve to get the answers.
Method 2: Anaylzing block, w.r.t wedge
W.r.t. M, m has only vertical acceleration which is a downward. Here we have to apply pseudo force(mA in figure) because M is non-inertial frame.
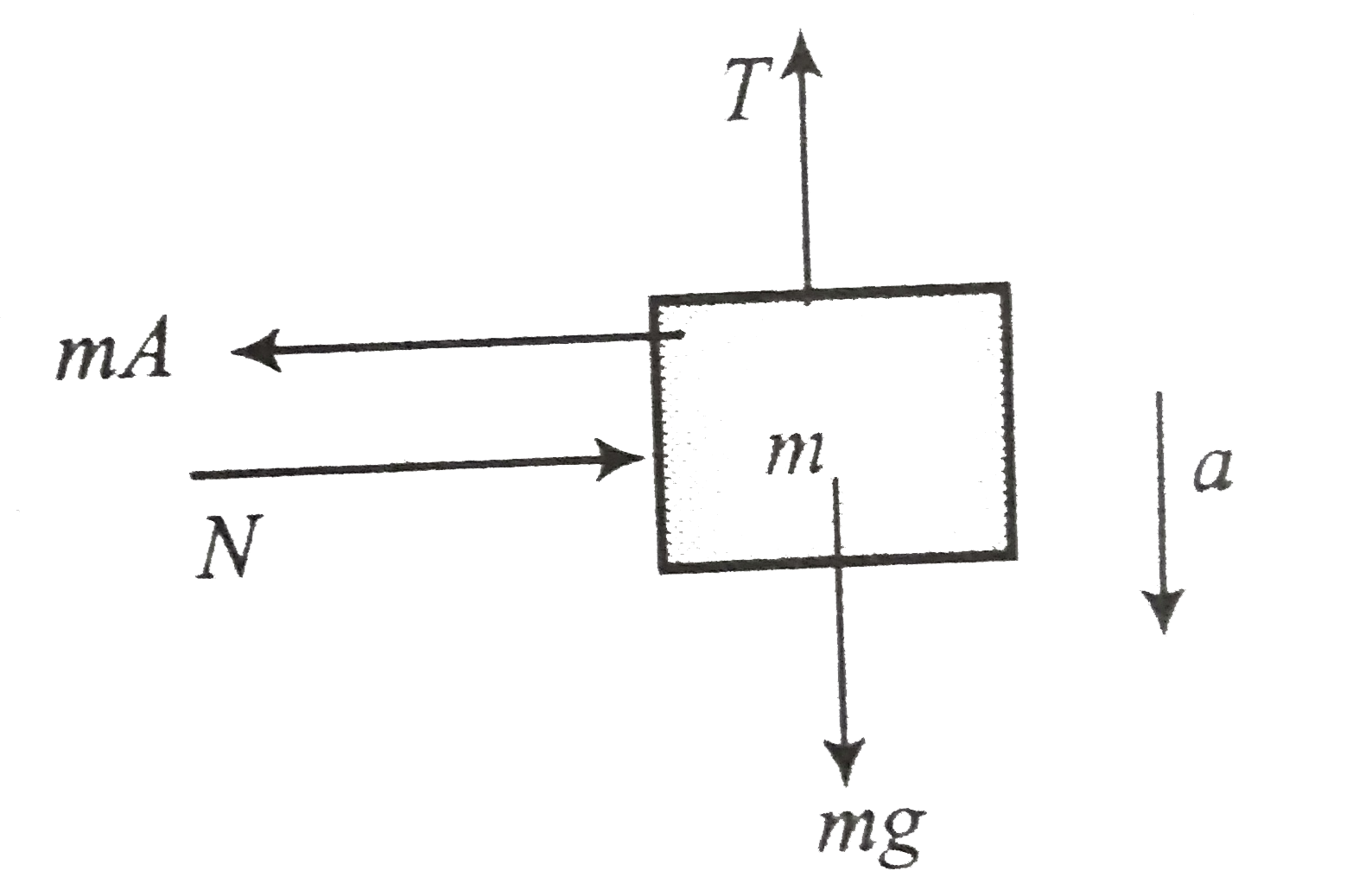
From FBD of w.r.t. M, writing the equation of motion of block:
N=mA,mg−T=ma
These equation are same as (vi) and (vii). solve to get answer.
Method 3: Consider the motion of m and M together in horizontal direction.
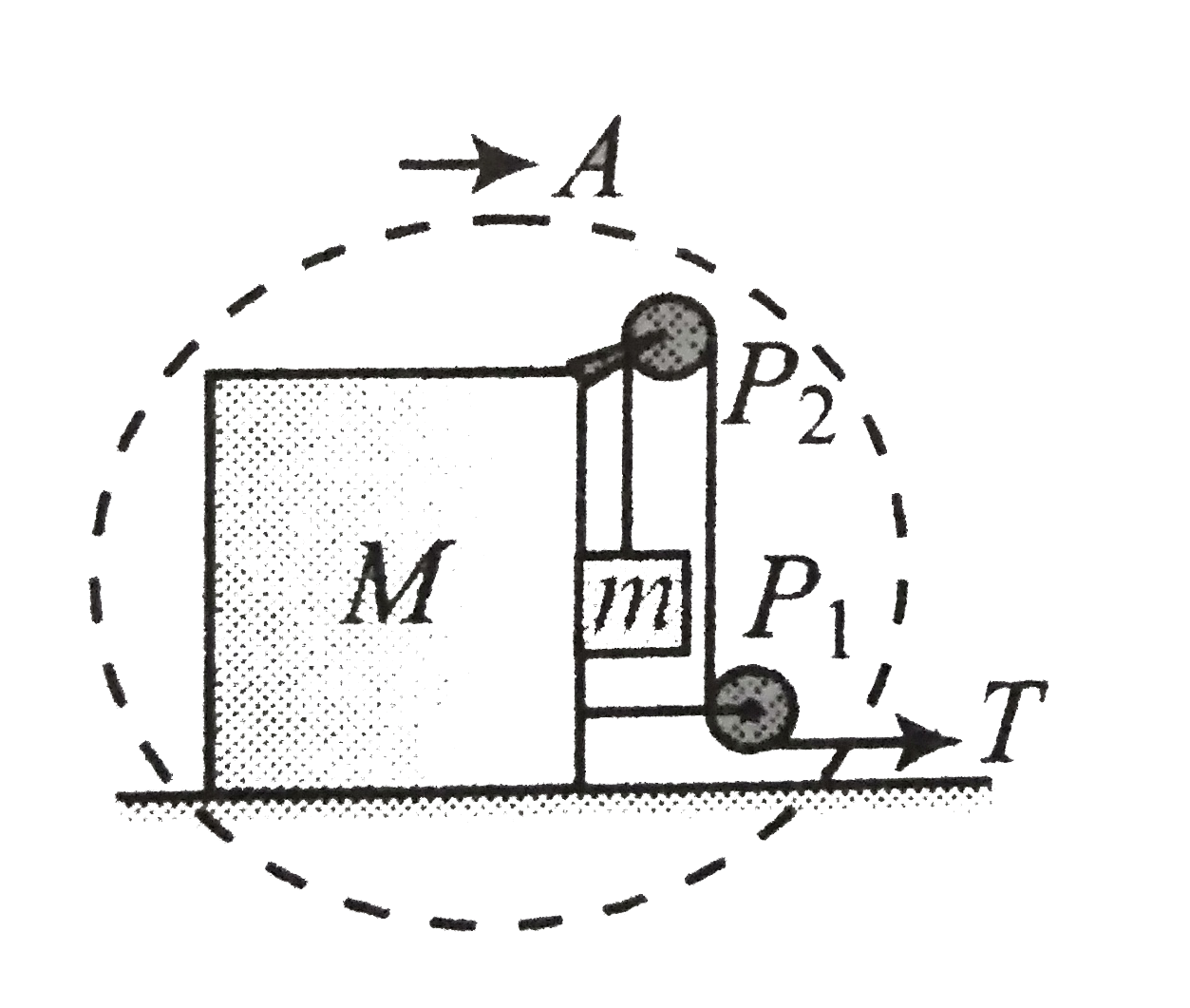
T=(M+m)A ...(vi)
Now consider the motion of m in vertical direction only
mg−T=ma=mA ...(vii)
From (iii)
T=m(g−A) ...(viii)
From (ii) and (iv)
m(g−A)=(M+m)A⇒A=mgM+2m=a
Hence, the net acceleration of m
anet=√a2+A2=√2A=√2mg(M+2m).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.235videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system.

The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle θ with horizontal. Find the acceleration of m and M after release.View SolutionFigure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
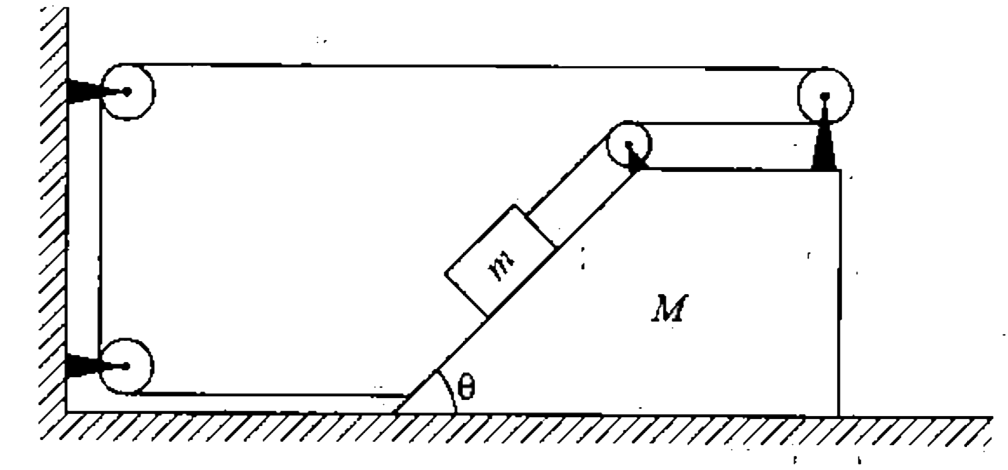 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-
 A√πRgB2√πRgC√2RgD√gR
A√πRgB2√πRgC√2RgD√gR - Question 2 - Select One
A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
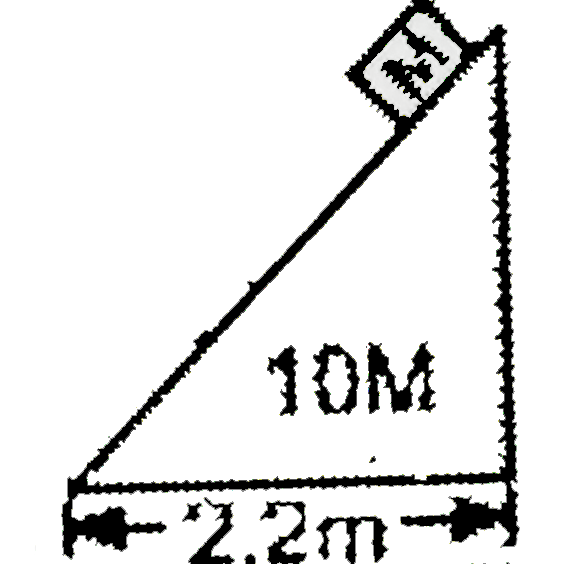 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 m - Question 3 - Select One
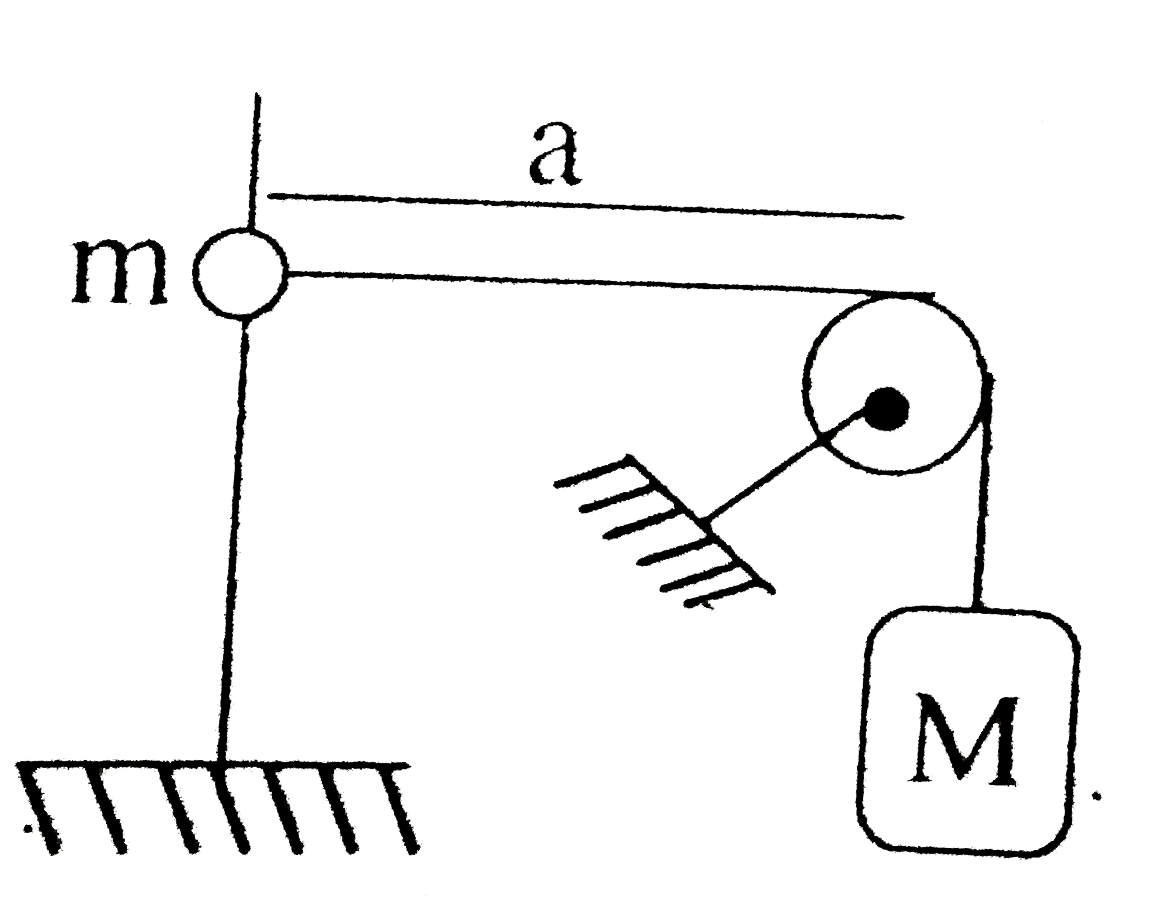
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string isAT=MgBT>MgCT<MgDT=Mg+Mg
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force P is applied at one end of rope. The force which the rope exerts on the block is:
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
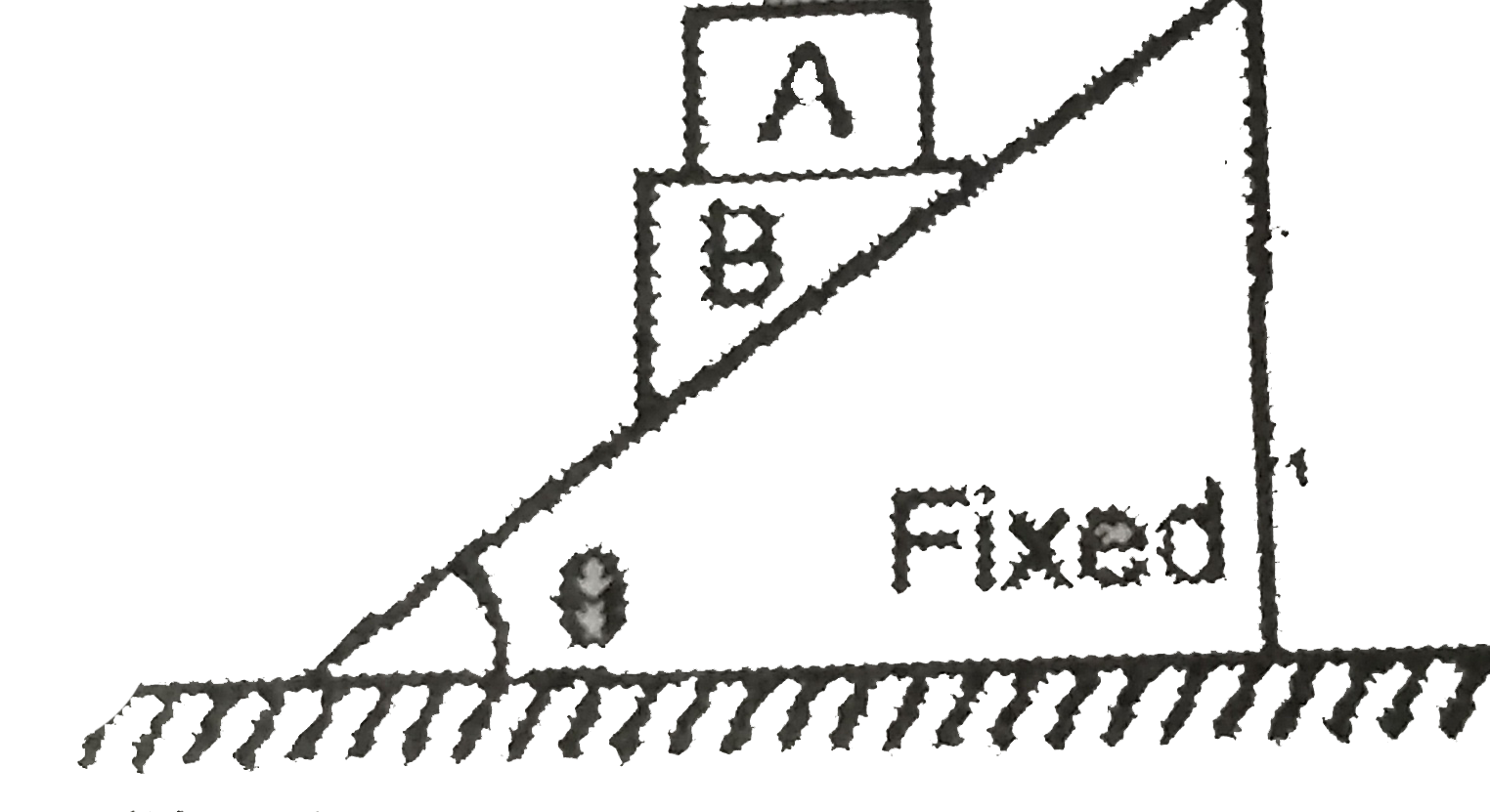 View Solution
View SolutionIn the system shown in fig., mA=4m, mB=3m, and mc=8m. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of block C isView SolutionIn the system shown in fig., mA=4m, mB=3m, and mc=8m. Friction is absent everywhere. String is inextensible and light. If the system is released from rest, then

Acceleration of Block B isView Solution

