The bobo of a pendulum at rest is given a sharp hit to impart a horizontal velocity u where l is the length of the pendulum. Find the angle rotated by the string before it becomes slack.
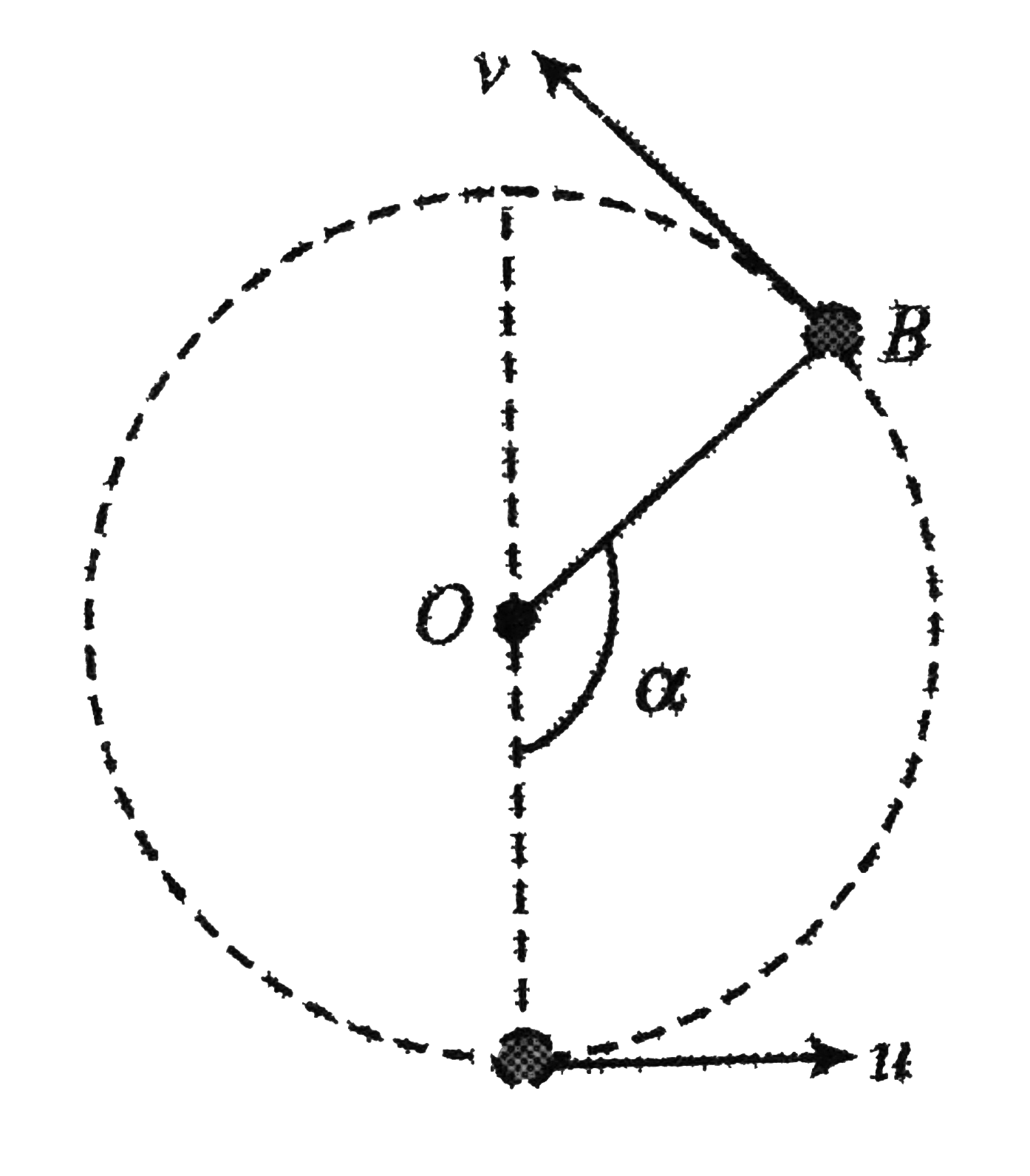
Let stirng slacks at B.
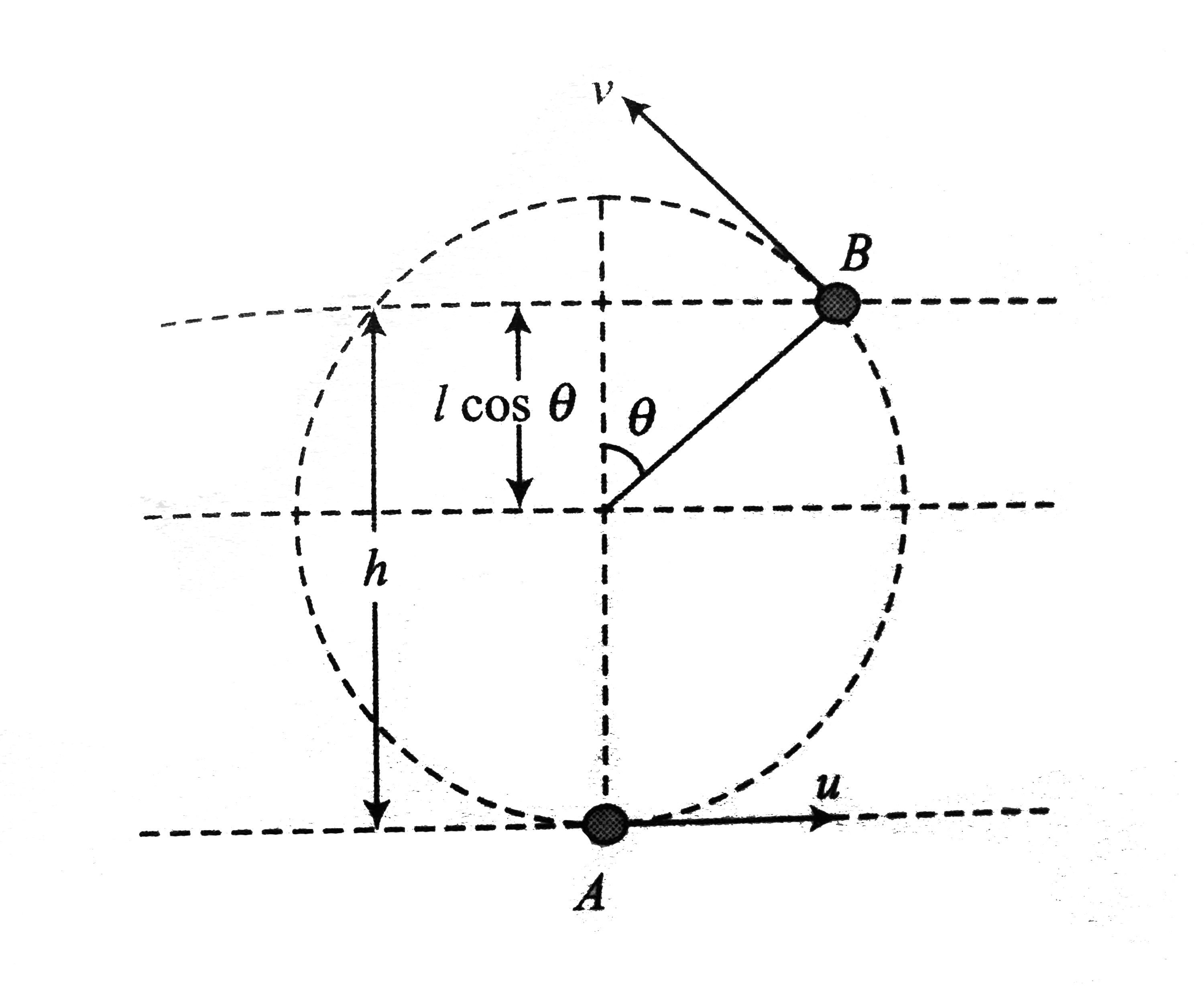
Applying COM, E at A and B, ΔU+ΔK=0
mgh+[12mv2−12μ2]=0
12mv2−12μ2=−mgh
v2=u2−2g(1+1cosθ)
When string slacks tension in the string becomes zero. The component of the weight in radial direction provide centripetal force at this position. From FBD of bob, we can write
mv2l=mgcosθ
v2=lgcosθ (ii)
From equation (i) and (ii), we get
3gl−2glcosθ=glcosθ
3cosθ=1⇒θ=cos−1(13)

Hence, the angle rotated by the string before it becomes slack is
⇒α=π−θ=π−cos−1(13)
Topper's Solved these Questions
Similar Questions
The bob of a pendulum at rest is given a sharp hit to impat a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with teh upward vertical.
View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
View SolutionThe bob of a simple pendulum is given a sharp hit impart it a horizontal speed of √3gL. Find an angle made by the string with the upper verticle before it becomes slack. Also, calculate the maximum height attained by the bob above the point of suspension. L is length of the string.
View SolutionThe bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.
 View Solution
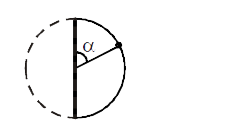
View SolutionThe bob of a simple pendulum of length l is given a sharp hit to impart it a horizontal speed of √3gl . When it was at its lowermost position. Find
angle α shown of the string from upside of vertical and speed of the particle when the string becomes slack.
 View Solution
View SolutionThe time period of a simple pendulum is given by T=2π√lg
where 'l' is the length of the pendulum and 'g' is the acceleration due to gravity at that place.
(a) Express 'g' in terms of T
(b) What is the length of the seconds pendulum ? (Take g=10ms−2)View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionThe time period of a simple pendulum is given by T=2π√lg
where 'l' is the length of the pendulum and 'g' is the acceleration due to gravity at that place.
(a) Express 'g' in terms of T
(b) What is the length of the seconds pendulum ? (Take g=10ms−2)View SolutionThe bob of a simple pendulum of length 1m hangs at rest. It is suddenly projected horizontally with velocity 10ms−1. Calculate the velocity of the bob and tension of the string when it is horizontal. The mass of the bob is 12kg.
[Hint : See worked out example 4]View Solution

