A block is projected with a speed v0 such that it strikes the point of projection after describing the path as shown by the dotted line. If friction exists for the parth of length d and the vertical circular path is smooth, assuming μ=coefficient of friction,
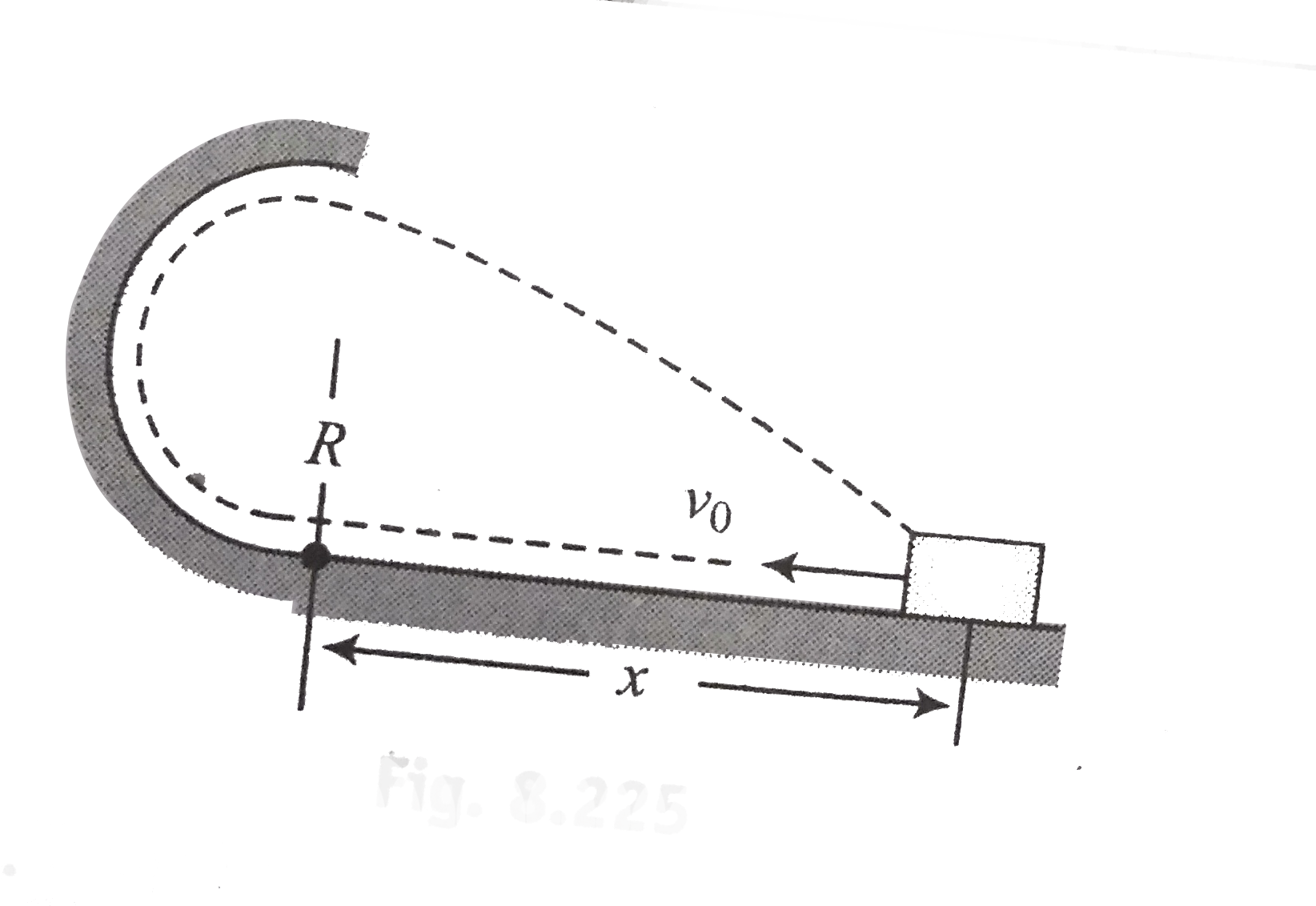
a. Find v0.
b. What is the minimum value of v0?
The correct Answer is:a. √d3g4R+2g[μd+2R]; b. √5gR
a. From C to A, time taken
t=√2[2R]g=√4Rg
v2=dt=d√g4R
From B to C, 12mv21=12mv22+mg(2R)
⇒v21=v22+4gR=d2g4R+4gR
From A to B: v21=v20−2μgdimpliesv20=v21+2μgd
⇒v0=√d2g4R+2g[μd+2R]
b. For minimum v0, v1=√5gR

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A block is projected with a speed v0 strikes the point pf projection after describing the path as shown in figure by dotted line. If friction exists for the path of length d and the vertical circular path is smooth, assuming coefficient of frictioin to be μ

(A) Find v0?
(B) What is the minimum value of v0 ?
View SolutionA car is moving in a horizontal level circular track with uniform speed v. If R is the radius of circular path, then the minimum coefficient of friction to avoid over turning is
View Solution
Knowledge Check
A particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
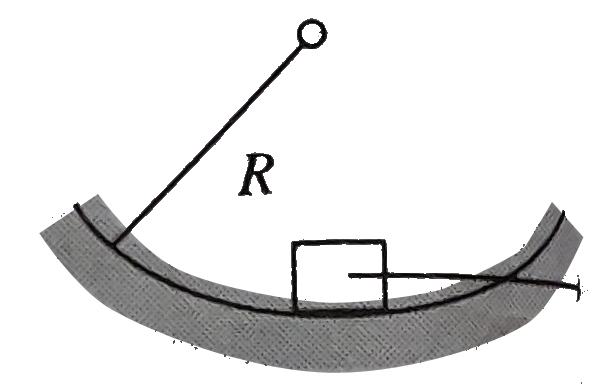 AgB√5g2C√2gDnone of these
AgB√5g2C√2gDnone of theseAt t=0, a block (of mass m) is projected with speed v on a rough long horizontal plank (of mass 3m) placed on smooth ground, as shown. Work done by friction on the block between t=0 and t=∞ equals :
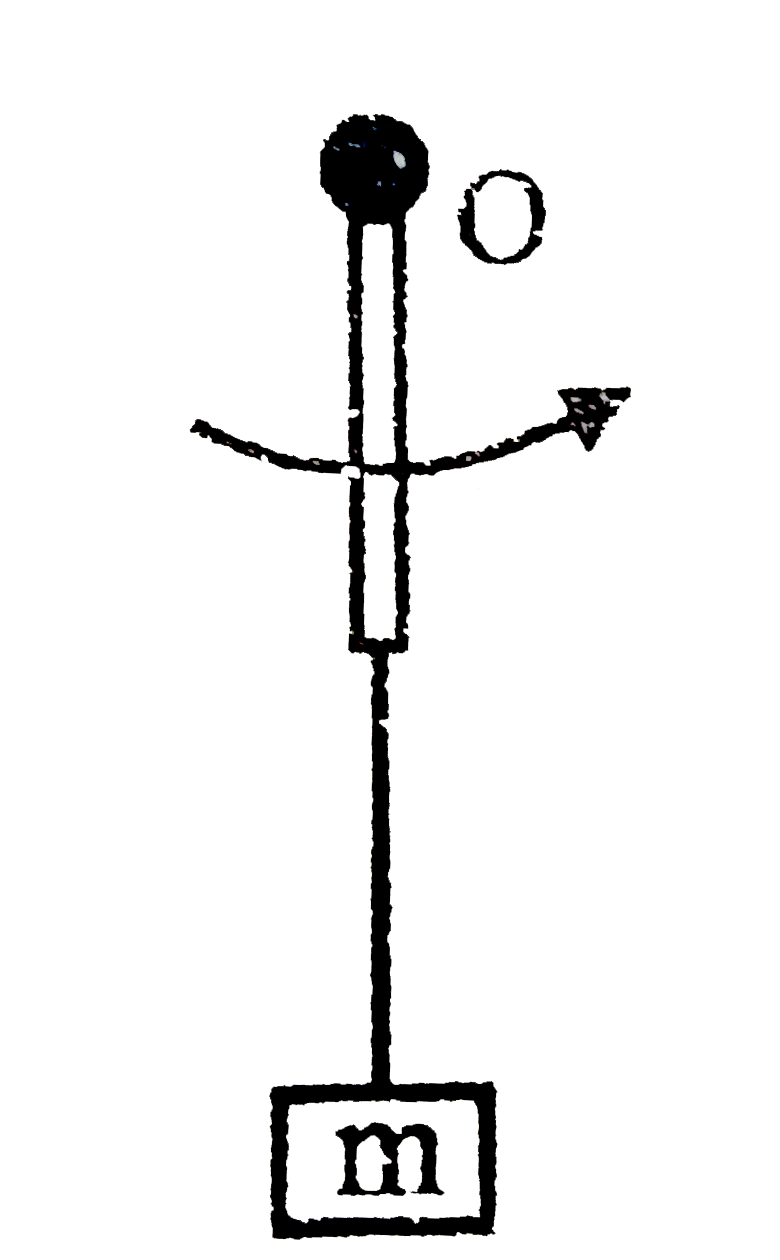 A15mv232B−15mv232C−3mv28D−mv216
A15mv232B−15mv232C−3mv28D−mv216A body is projected horizontally with a speed v0 find the velocity of the body when it convers equal distance in horizontal and vertical directions.
Av=2v0Bv=√5v0Cv=v02Dv=√3v0
A particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View SolutionA particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
View SolutionA body is projected vertically upwards with a speed v0. Find the magnitude of time average velocity of the body during its ascent.
View SolutionA body is projected up with a speed v0 along the line of greatest slope of an inclined plane of angle of inclination β. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
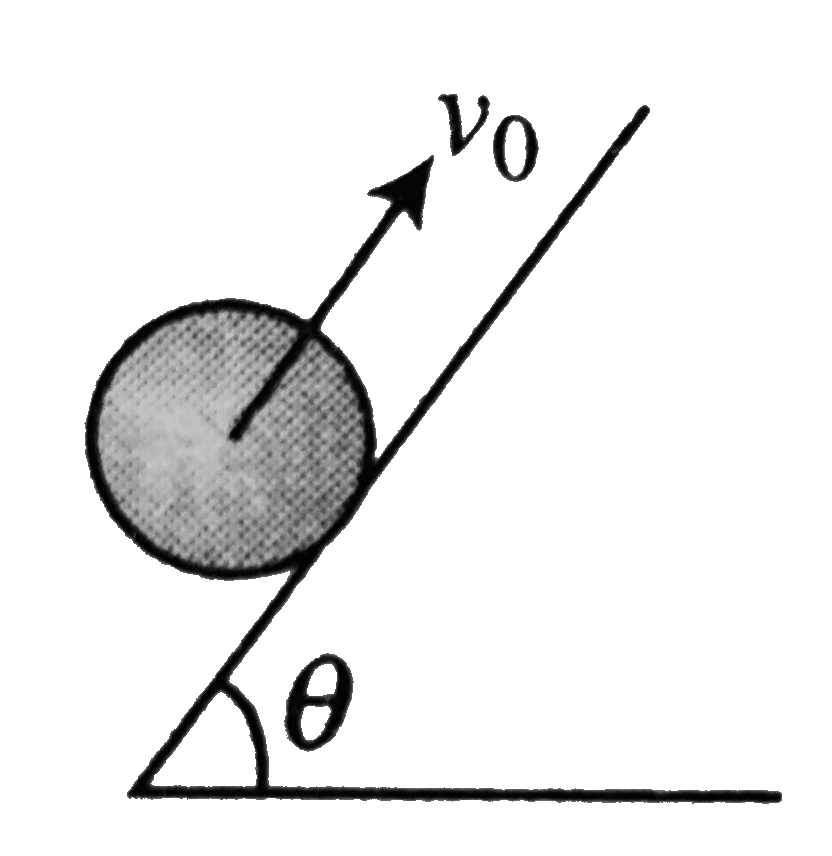
View Solution