A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
b. What will be the highest point from the lowermost point of circular track, to which it will rise?
The correct Answer is:a. cos−1(2/3); b. 50l54
If at point P, tension is zero. Then
mgcosθ=mv2r
Using conservation of energy, v2=gl(1−cosθ)
∴mgcosθ=mgll/2(1−cosθ)
⇒θ=cos−1(2/3)
Therefore, height of point,
P=l2+l2cosθ=5l6,
from lowest point
v2=gl(1−23)=gl3⇒v=√gl3
Now the particle describes parabolic path.
The height attained by the particle, from point P.
h=(vsinθ)22g=5l54
Therefore, highest point from loweset point will be
(5l6+50l54)=50l54

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A . The ball is drawn aside so that the thread taken up a horizontal position at the level of point O and then released. Find
(a) A what point of the ball's trajectory, will the tension in the thread disappear?
(b) What will be the highest point to which it will rise?
View SolutionA small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be imparted to the ball so that it could deviate through the maximum angle π/2 in the process of motion?
View Solution
Knowledge Check
A small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
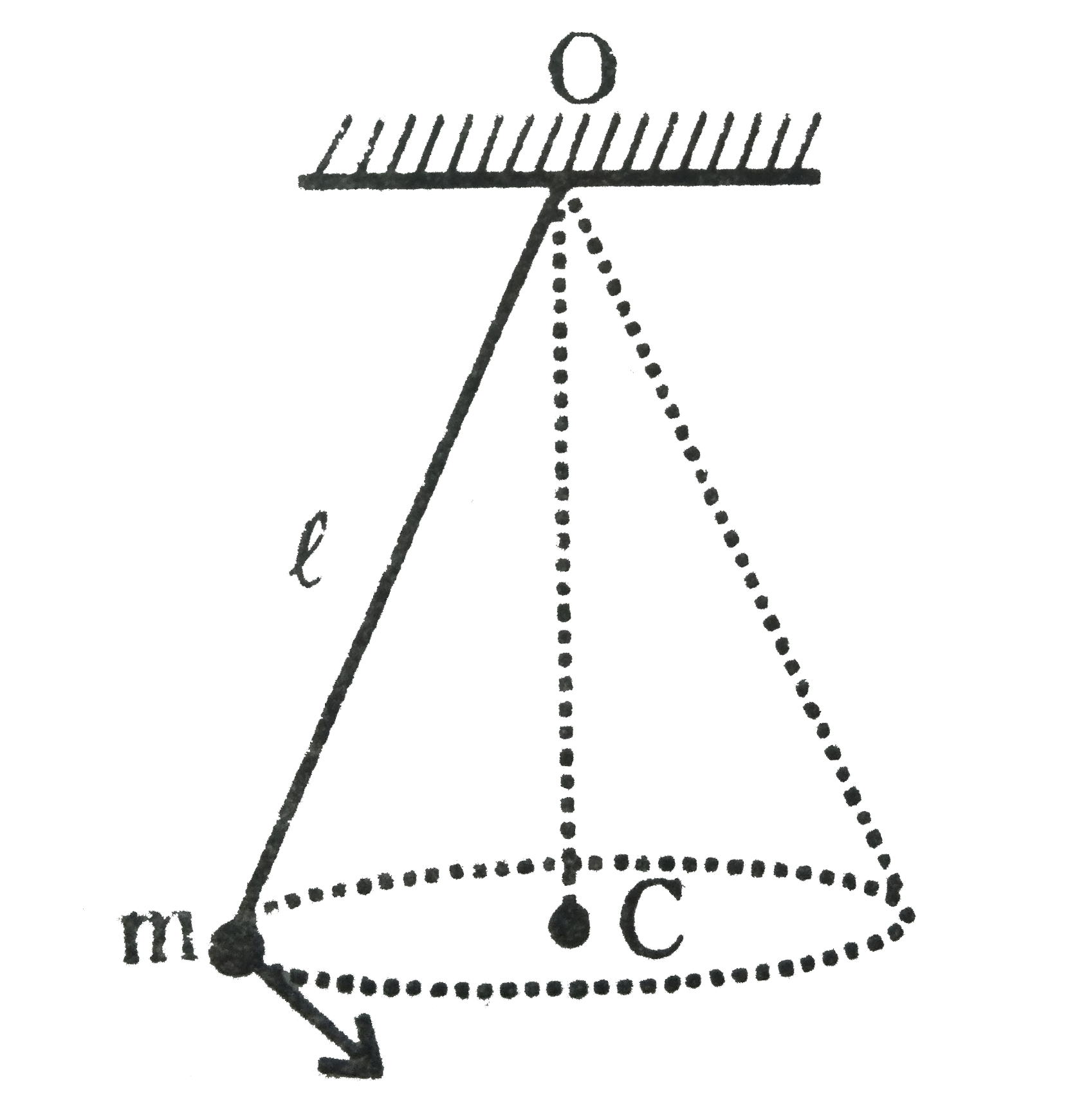 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conservedA spere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
A√5 glB2 glC√glD√2glA spere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
AglB2glC√glD√2gl
A simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.

View SolutionA small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Relative to which points does the angular momentum M of the ball remain constant? Find the magnitude of the increment of the vector of the ball's angular momentum relative to the point O picked up during half a revolution.
View SolutionA sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View Solution
