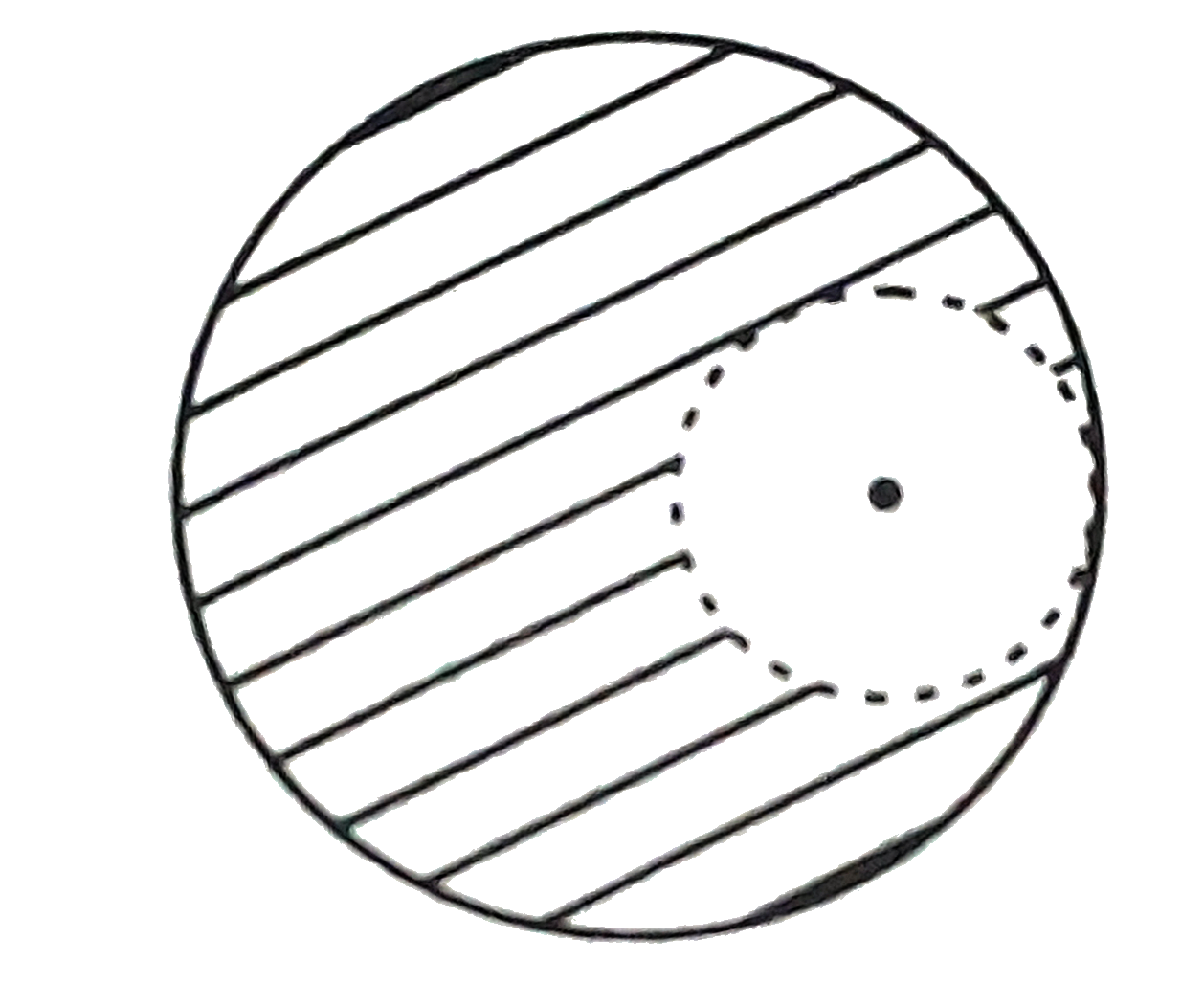
From a solid spere of mass M and radius R a sperhical poriton of radius is removed as show in the taking gravitational potential V=0 at the potential at the centre of the cavity thus formed (G= gravitonal constant )
The correct Answer is:B
Consider cavity as negative mass and apply superposition of gravitational potential consider the cavity formed in a soid spher as show in

Accroding to the question we can write potential at an internal point P due to complete solid sphere
Mass of removed part
bus potential due to remaining part at point P
Topper's Solved these Questions
- GRAVITATION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner
20 Videos
- GRAVITATION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - Exercise 1
69 Videos
- FRICTION IN SOLID AND LIQUIDSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)
24 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
Similar Questions
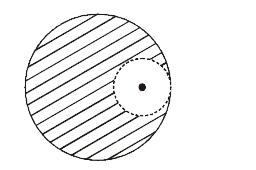
From a solid sphere of mass M and radius R, a spherical portion of radiu R2 is removed as shown in the figure. Taking gravitational potential V = 0 at r=∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)
View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View Solution
Knowledge Check
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A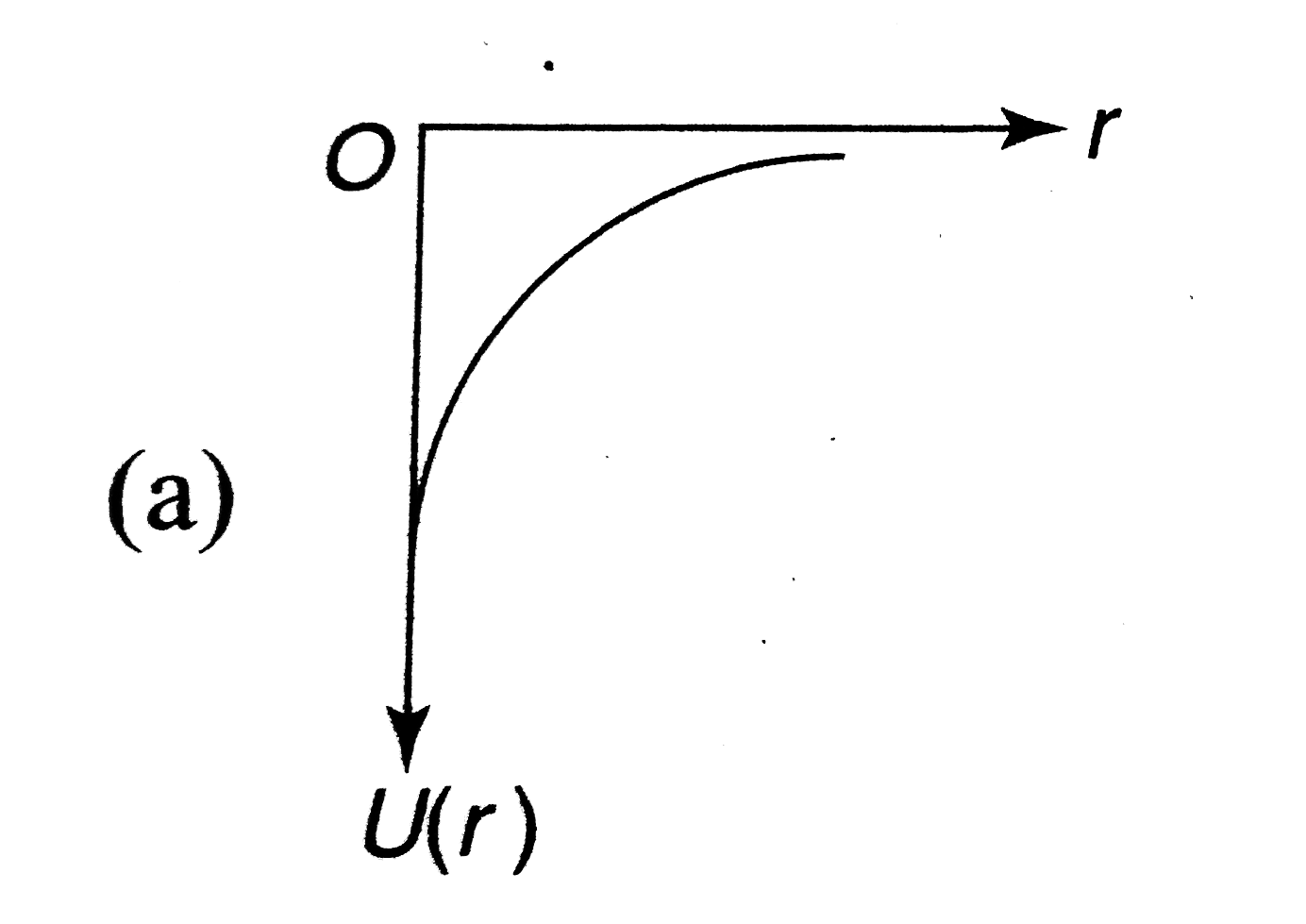 B
B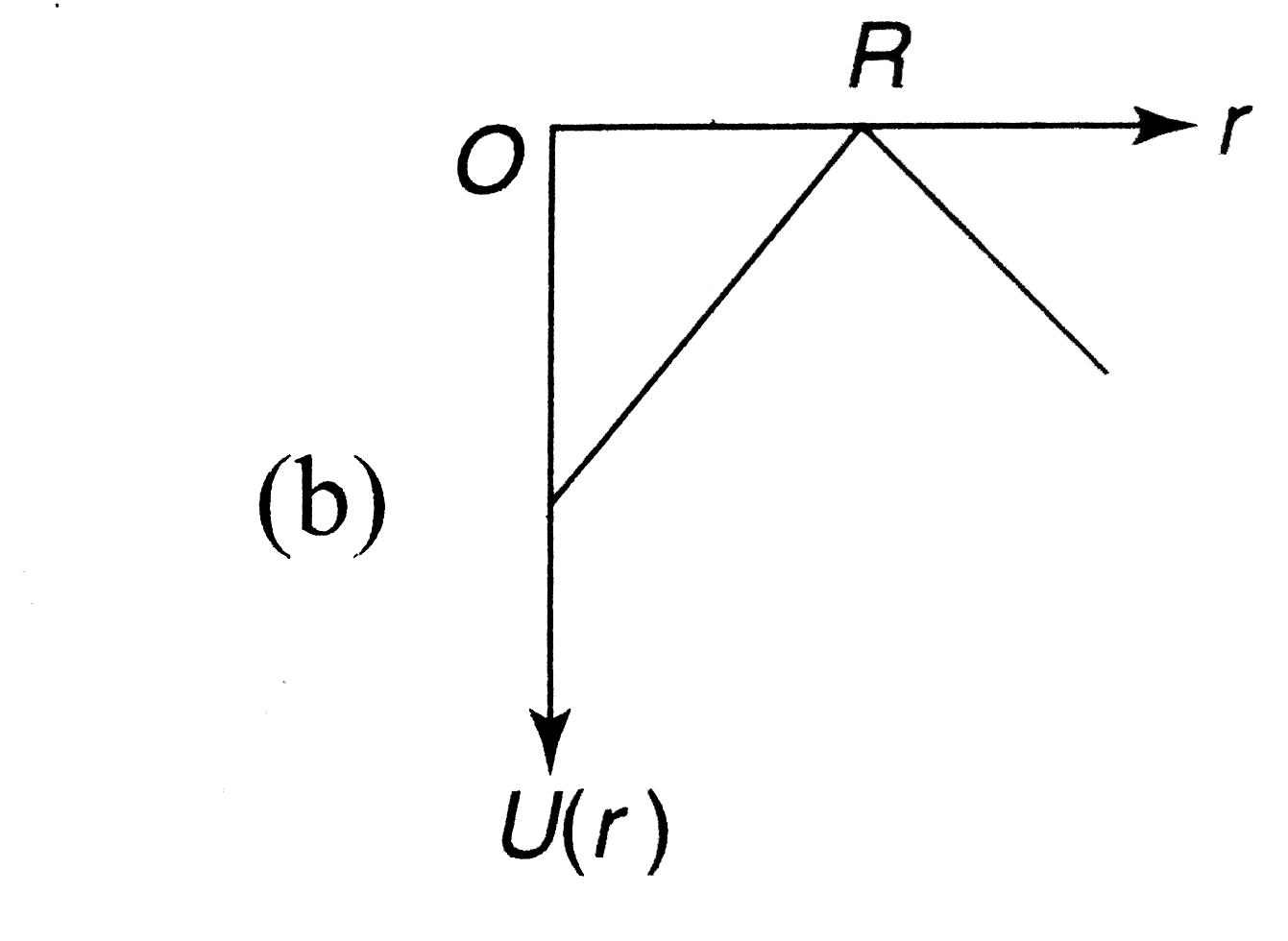 C
C D
D
Find the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
View Solution
