Two plates of same thickess with thermal conductivities $k_{1} and k_{2}$ and area of cross - sections $A_{1} and A_{2}$ are connected (as shown in figure ) for heat conduction . The equivalent coefficient of thermal conductivity (k) will be

A

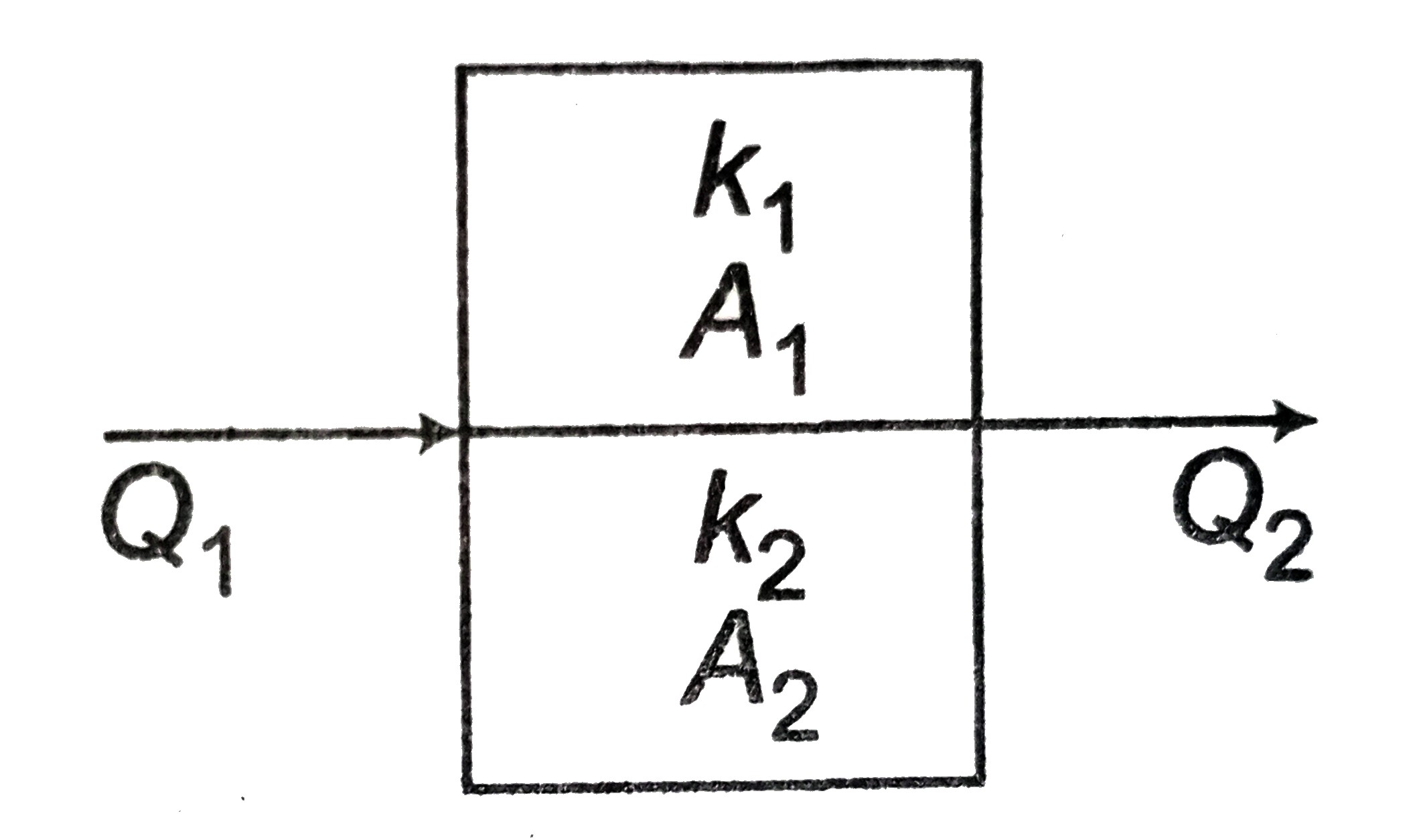
$k_{1} + k_{2}$

B

$\frac{k_{1} + A_{2}}{A_{1}} + \frac{k_{2} + A_{1}}{A_{2}}$

C

$\frac{k_{1} + A_{1}}{A_{1} + A_{2}} + \frac{k_{2} A_{2}}{A_{2} + A_{2}}$

D

$\frac{k_{1} + A_{2}}{A_{1} + A_{2}} + \frac{k_{2} A_{1}}{A_{1} + A_{2}}$

Text Solution

Verified by Experts

The correct Answer is:C

Total heat current , $\frac{d Q}{d t} = \frac{d Q_{1}}{d t} + \frac{d Q_{2}}{d t}$
$\Rightarrow \frac{K (A_{1} + A_{2})}{d x} = K_{1} A_{1} \frac{d T}{d x} + K_{2} A_{2} \frac{d T}{d x}$
$\Rightarrow k = \frac{k_{1} A_{1} + k_{2} A_{2}}{A_{1} + A_{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS KINETIC THEORY OF GASES ANDRADIATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $K_{1} + K_{2}$
B $\frac{(K_{1} + K_{2})}{2}$
C $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
D $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $K_{1} + K_{2}$
B $\frac{(K_{1} + K_{2})}{2}$
C $\frac{K_{1} + K_{2}}{K_{1} + K_{2}}$
D $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $\frac{K_{1} + K_{2}}{2}$
B $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
C $\frac{K_{1} + K_{2}}{3}$
D $\frac{3 K_{1} + K_{2}}{K_{1} + K_{2}}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-KINETIC THEORY OF GASES ANDRADIATION-Exercise 2

Home
Ask Doubt
Profile