In the figure shown, initially the spring is in relaxed position. A bullet of mass m hits the block 'A' with horizontal speed and gets embedded into it. Find the maximum compression in the spring. Stiffness of the spring is K. Neglect any friction and deformation in the spring during collision.
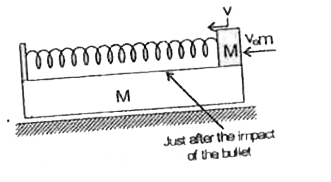
Since no external force is associated with the system conservation of horizontal momentum of the system yields.
Where velocity of (M+m) just after the impact & velocity of (M+M+m) just of the maximum compression of the spring.
The loss of K.E. between the two portion (a) and (b) is given as,

From conservation of mechanical energy
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE)
18 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

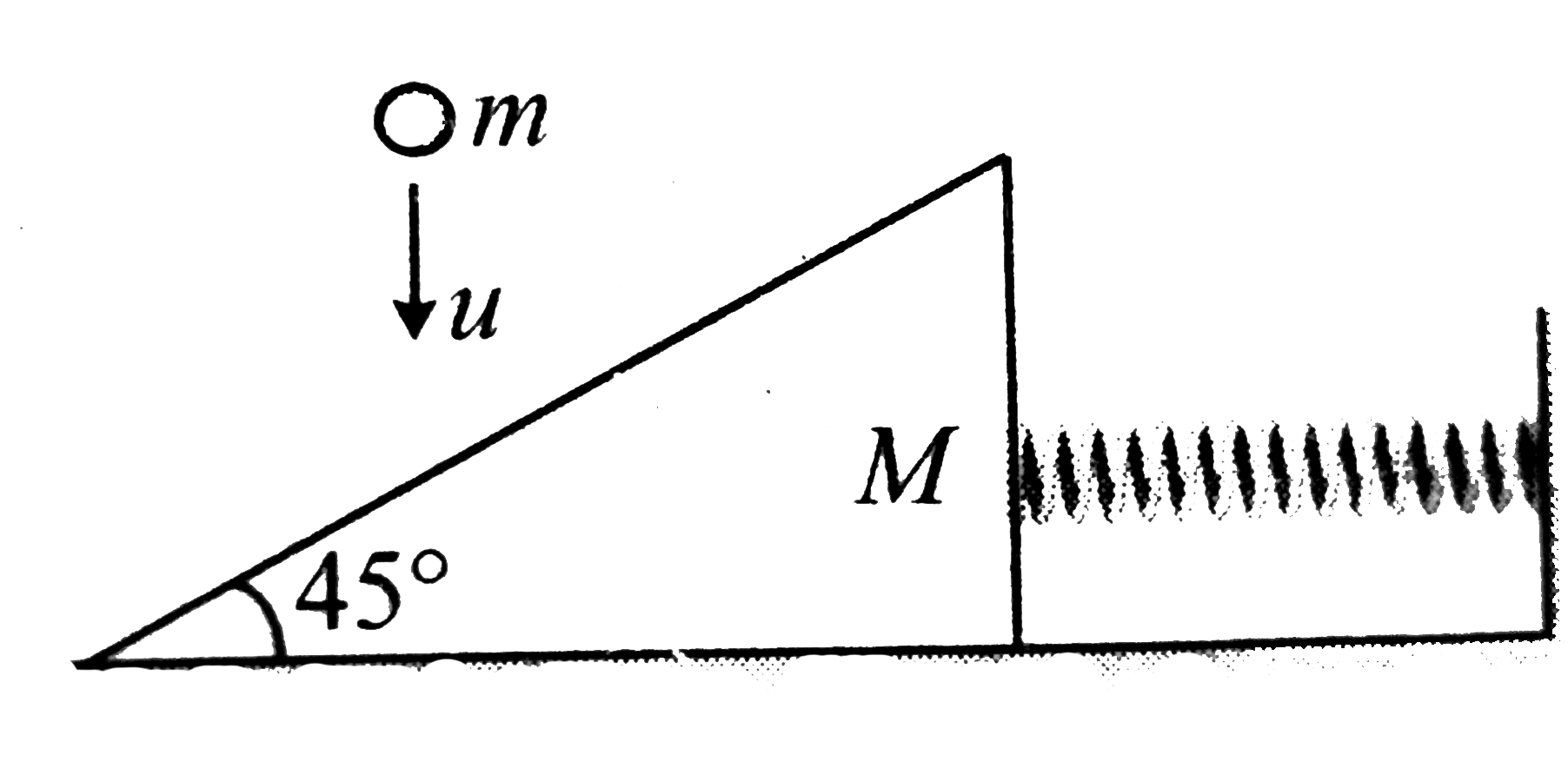
View SolutionA ball of mass m hits a wedge of mass M vertically with speed u, which is placed, on a smooth horizontal surface. Find the maximum compression in the spring, if the collision is perfectly elastic and no friction any where. Spring constant of spring is K.
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0For shown situation find the maximum elongation in the spring. Neglect friction everywhere. Initiallthe blocks are at rest and spring is unstreched.
 A4F3KB3F4KC4FKD2FK
A4F3KB3F4KC4FKD2FK
A ball of mass m hits a wedge of mass M vertically with speed u, which is placed, on a smooth horizontal surface. Find the maximum compression in the spring, if the collision is perfectly elastic and no friction any where. Spring constant of spring is K.

View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
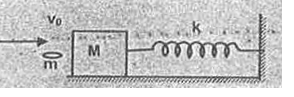
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.

View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.

View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View Solution
