A plank of mass M, whose top surface is rough with coefficient of friction μ is placed on a smooth ground. Now a disc of mass m=M/2 and radius r is placed on the plank. The disc is now given a velocity v0 in the horizontal direction at t=0

a. Find the time when the disc starts rolling
b. Find the velocity of the plank and the disc up to that time.
c. Find the distance travelled by the plank up to this instant.
Find the work done by the friction force up to this instant.
a. Step 1: Free body diagram

b. Step 2: Equation of motion
For the plank: μmg=MA
⇒A=μmgM (towards right) …………i
⇒A=μg2 (as m=M2) (will be positive)
For the disc: μmg=ma
a=μg (backwards, towards left) (will be negative)
c. Step 3: Torque equation
μmgR=Iα
μmgR=mR22α
α=2μgR (clockwise) (will be positive)
d. Step 4: Constraint relations
At the time of rolling point P should not slide with respect to the plank.

−ωR
(0+at)=(v0−a)−(0+αt)R
Now substituting the values of A and a, we can calculate t,
μmgMt(v0−μ>)−(2μgRt)R
(μmgM+μg+2μg)t=v0
Which gives t=v0μg(mM+3)=v05μg (as m=M/2)
Velocity of the plank when rolling starts
V=At=(μg2)(v05μg)=v010
Velocity of the disc when rolling starts
v=v0+at=v0+(−μg)(v05μg)=45v0
Angular velocity at time of rolling,
ω=αt=(2μgR)(v05μg)=25v0R
Distance travelled by the plank,
Splank=12At2=12(μg2)(v05μg)2=v20100μg
Work done by friction force,
Wfriction=△Ktranslation+△Krotation
=[△Kdisc+△Kplank]translation+△Krotation
[(12mv2−12mv20)+(12MV2−0)(12Iω2−0)]
substituting the vaues of v,V and ω, we get the work done by friction i.e.,
Wfriction=13200Mv20
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionA solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,

View Solution
Knowledge Check
A ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
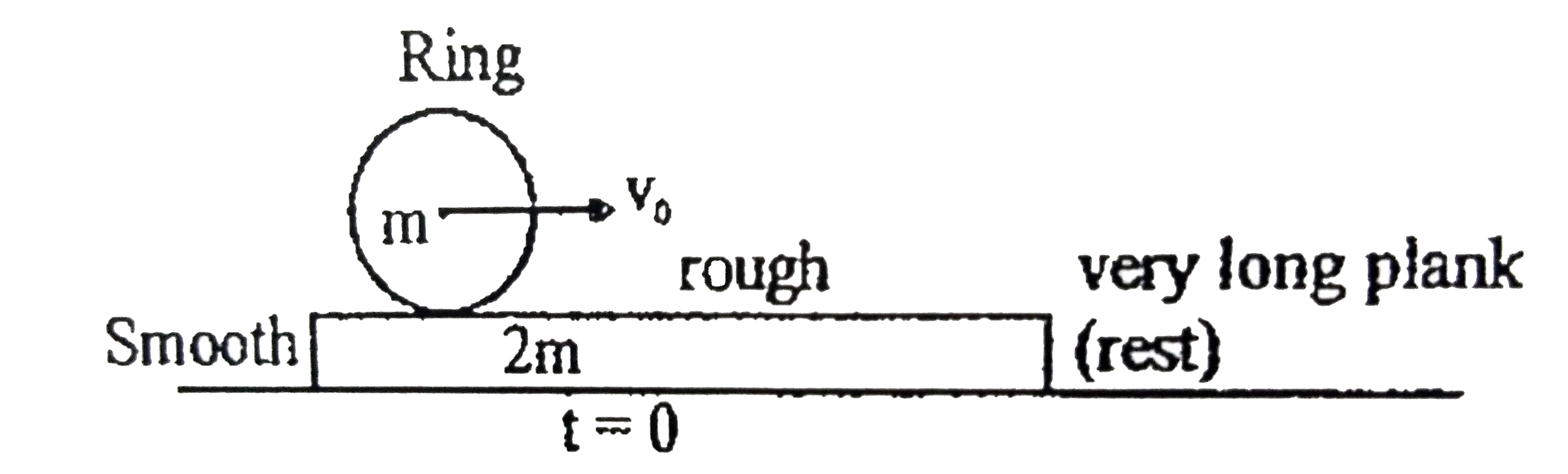 Av0μgBv04μgCv03μgD2v05μg
Av0μgBv04μgCv03μgD2v05μgA block of mass m is placed gently onto a long plank of mass M moving with a velocity v0 on a smooth horizontal floor. If friction is present between M and m :
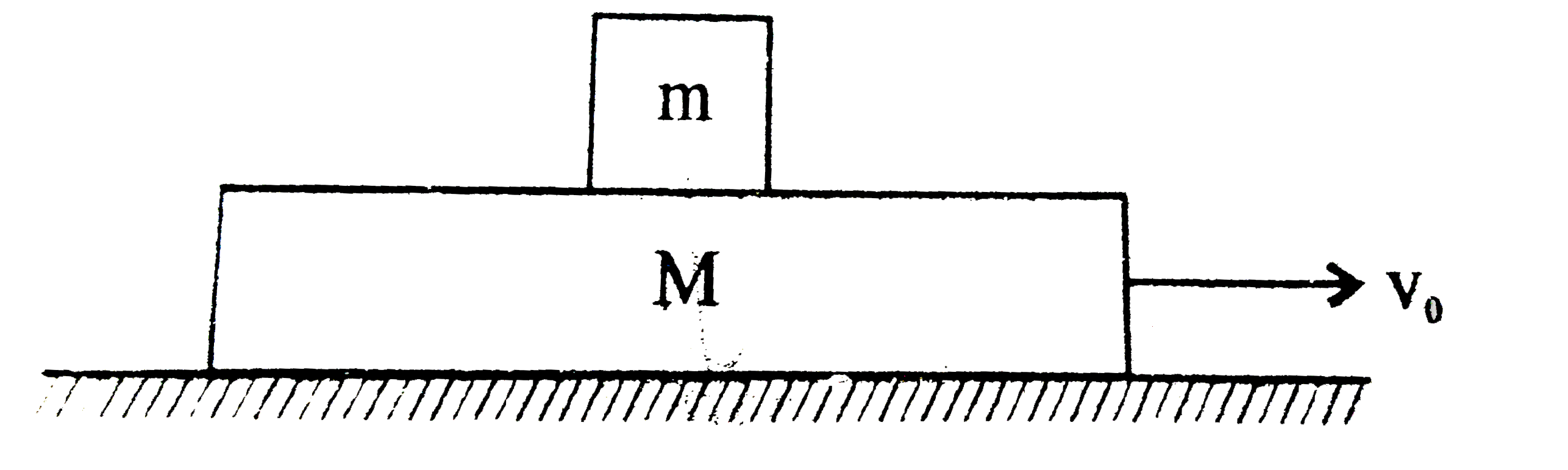 Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
A solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA plank of mass M is moving on a smooth horizontal surface with speed 'v0'. At t=0 a sphere of mass 'm' and radius 'r' is gently placed on it and simultaneously a constant horizontal force 'F' is applied on the plank in the opposite direction of v0. Find the time at which sphere starts rolling on the plank. The coefficient of friction between the plank and the sphere is μ.

View SolutionA man of mass m moves on a plank of mass M with a constant veloicty u with respect to the plank, as shown in figure.
a.If the plank rest on smooth horizontal surface, determine the velocity of the plank.
b If the man travels a distasnce L with respect to the plank, find the distance travelled by the plank with respect to te ground.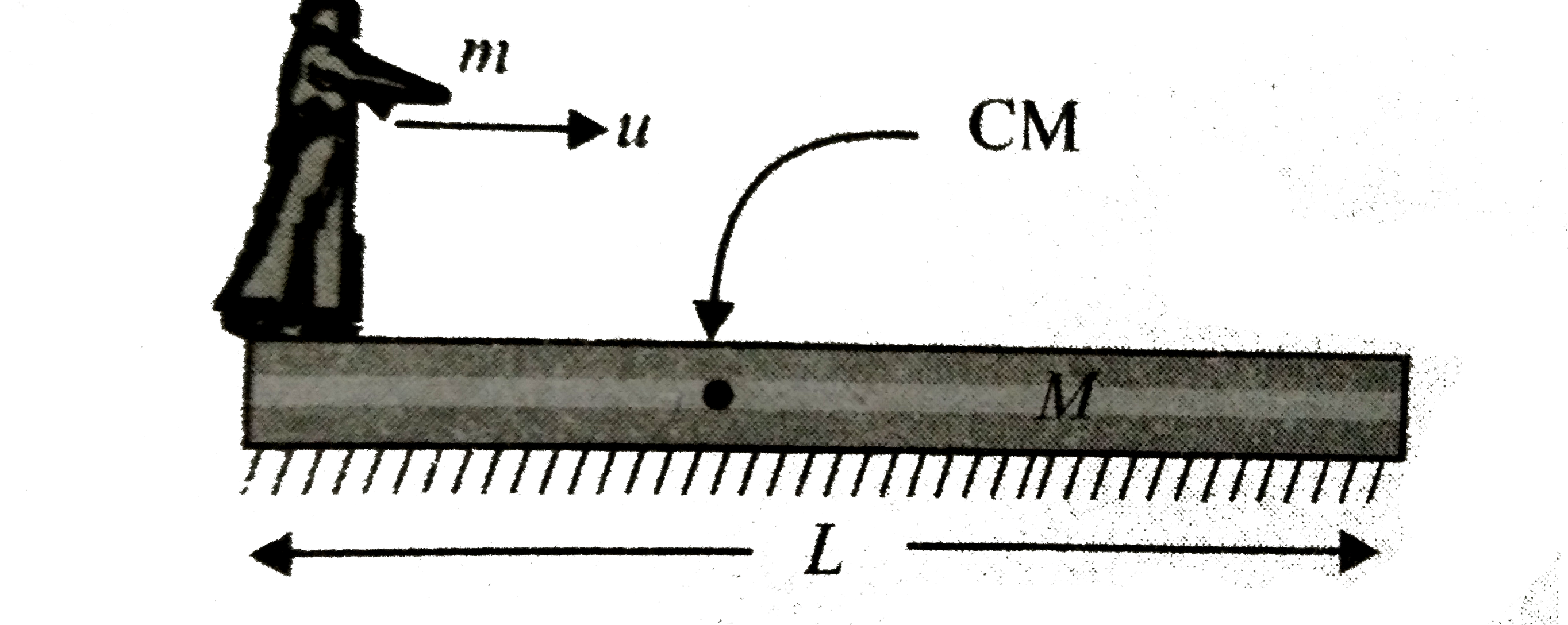
View SolutionA man of mass m moves on a plank of mass M with a constant veloicty u with respect to the plank, as shown in figure.
a.If the plank rest on smooth horizontal surface, determine the velocity of the plank.
b If the man travels a distasnce L with respect to the plank, find the distance travelled by the plank with respect to te ground.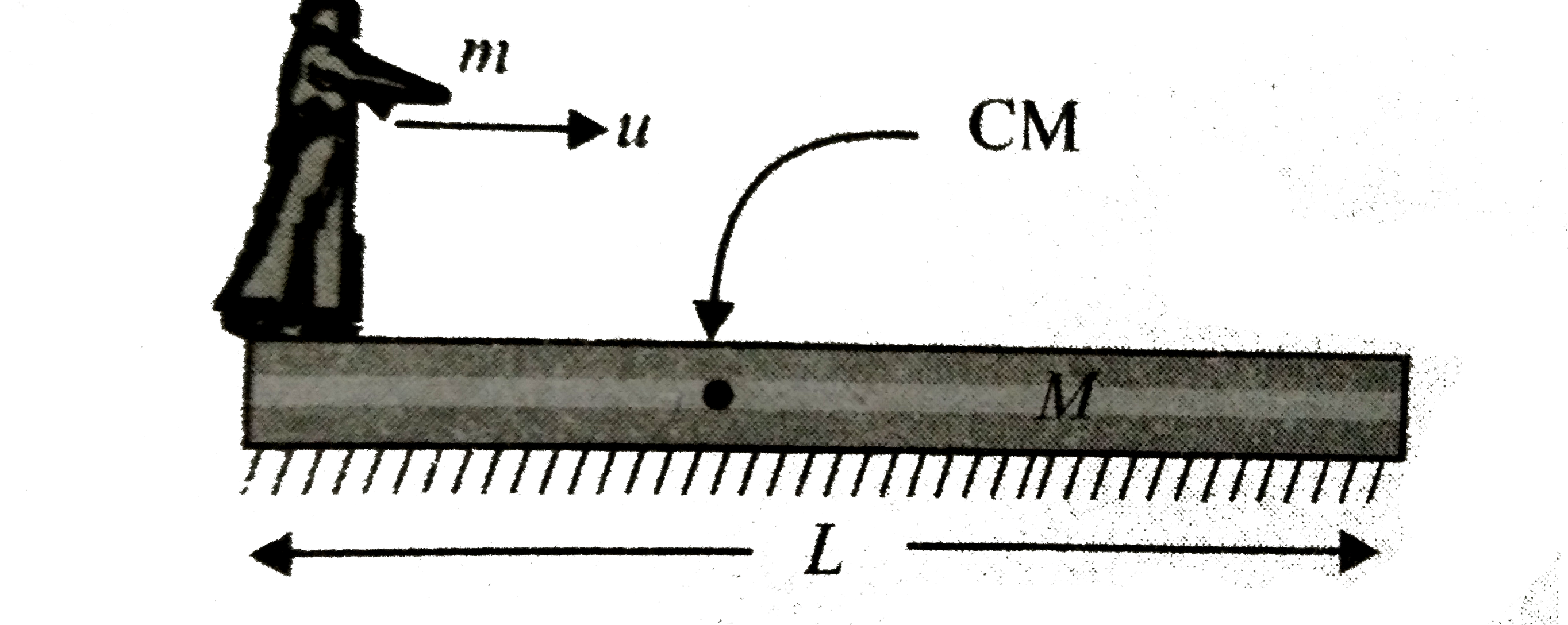
View Solution
