A plank of mass M is moving on a smooth horizontal surface with speed 'v0'. At t=0 a sphere of mass 'm' and radius 'r' is gently placed on it and simultaneously a constant horizontal force 'F' is applied on the plank in the opposite direction of v0. Find the time at which sphere starts rolling on the plank. The coefficient of friction between the plank and the sphere is μ.

Till rolling starts kinetic friction acts on the bodies.
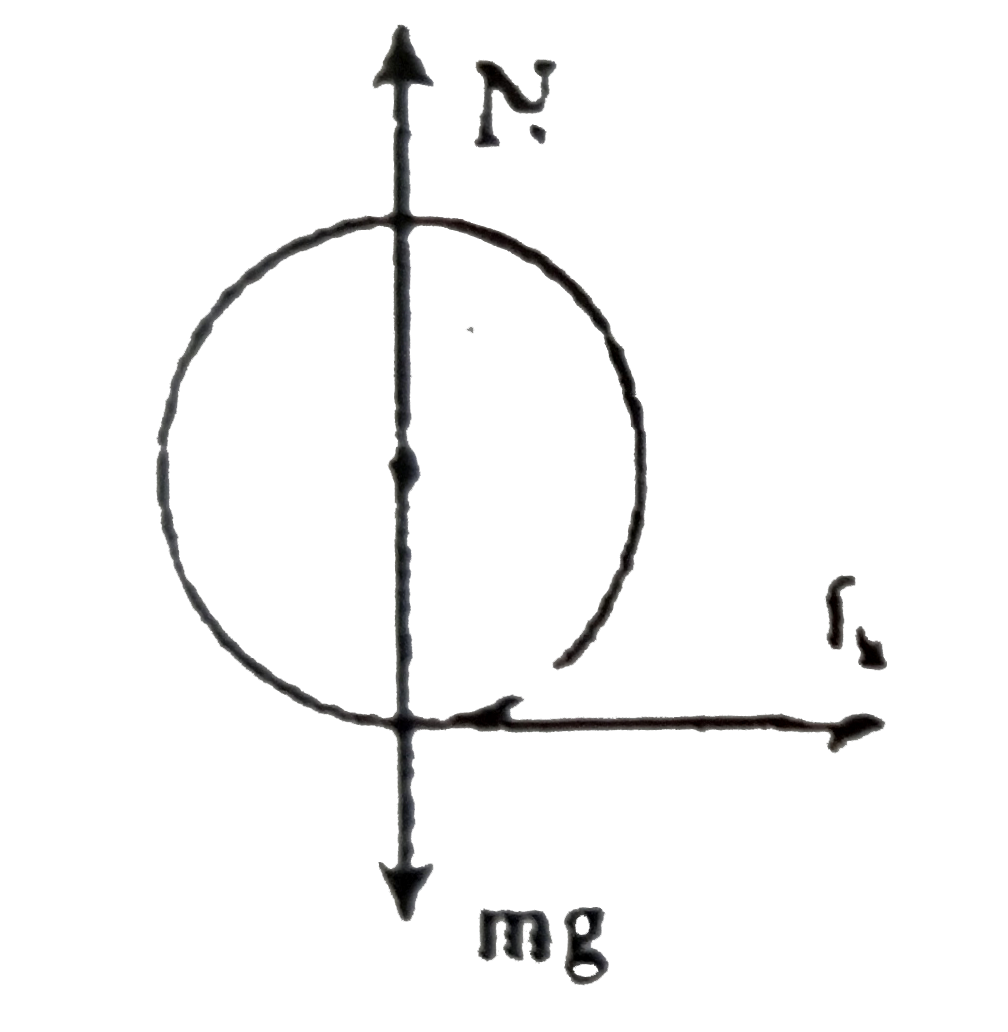
F.B.D. of sphere for no vertical acceleration N=mg….(1)
⇒fk=μmg(as fk=μN)
⇒a=μg
v=μgt
Also α=μmgrI⇒ω=μmgrtI
The velocity of the lower point of the sphere at time t is
vs=v+ωr
vs=μgt+μmgr2It
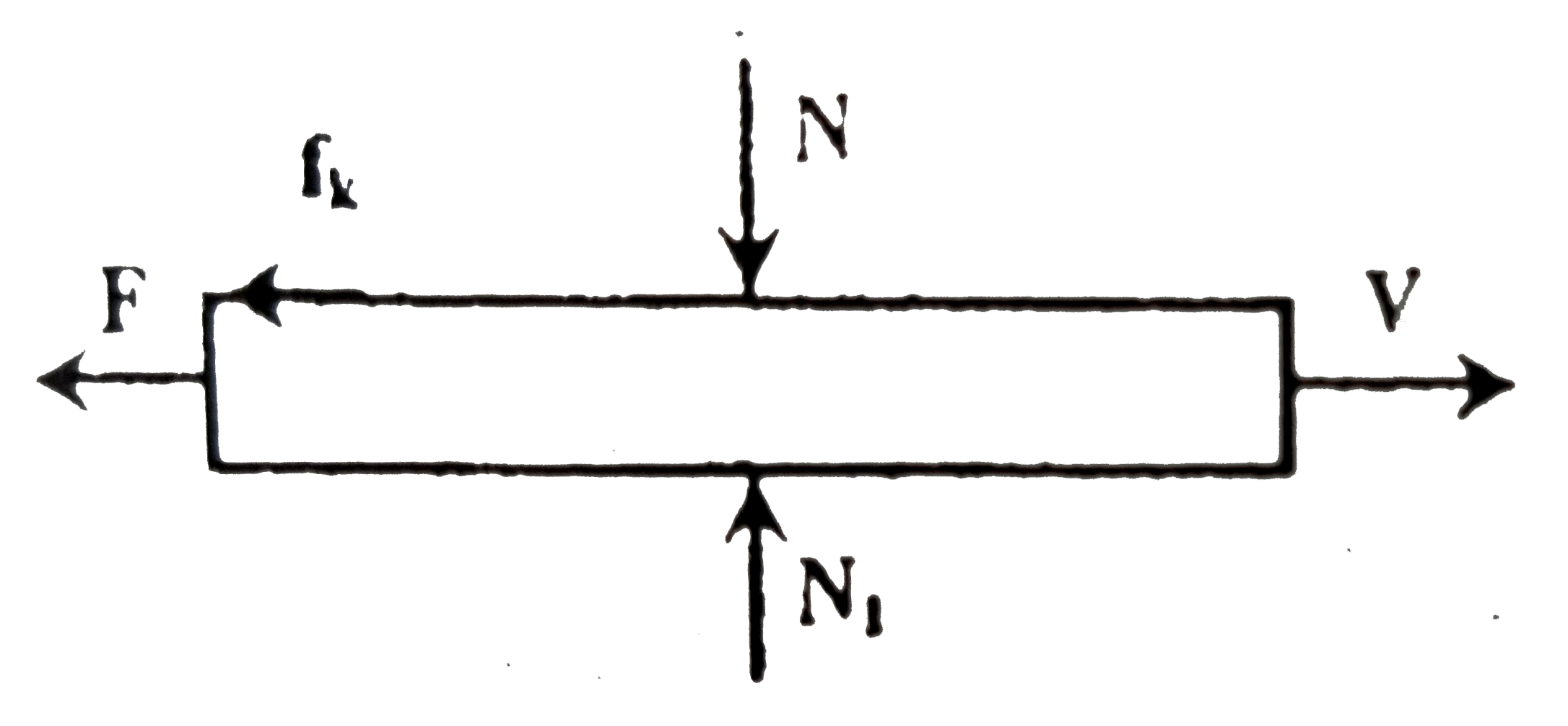
The F.B.D. of the plank
⇒aP=−(F+fkM)=−(F+μmgM)
vP=v0−(F+μmgM)t
For no slipping vs=vP
⇒μgt+μmgr2It=v0−(F+μmgM)t
⇒t=v0[72μg+(F+μmgM)]
Topper's Solved these Questions
Similar Questions
A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionA plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View Solution
Knowledge Check
- Question 1 - Select One
A ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
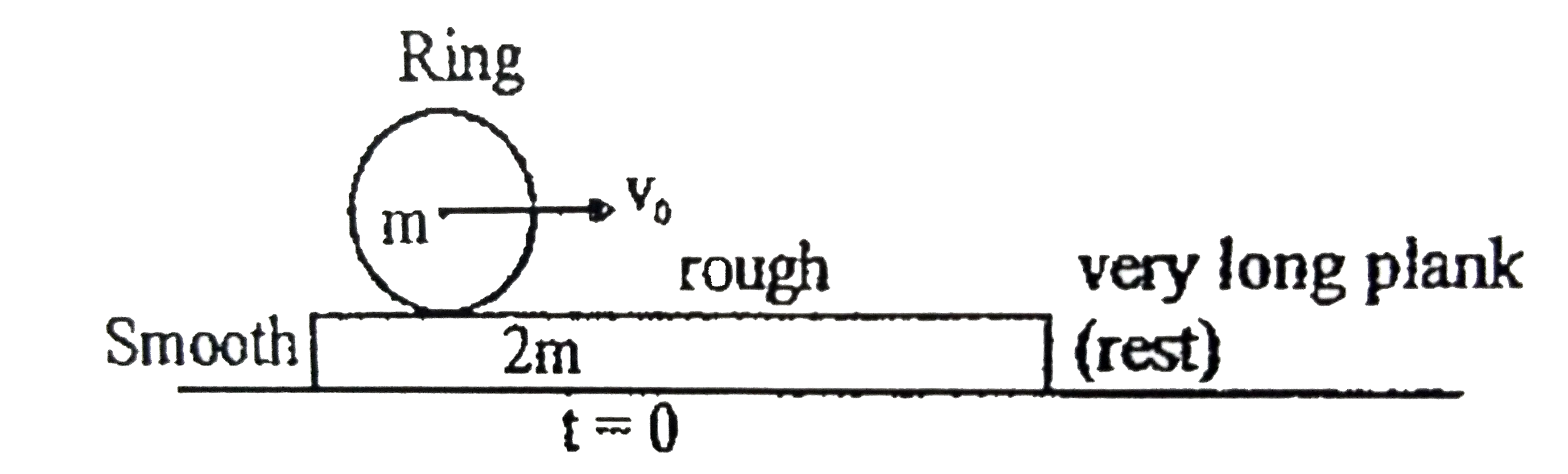 Av0μgBv04μgCv03μgD2v05μg
Av0μgBv04μgCv03μgD2v05μg - Question 2 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
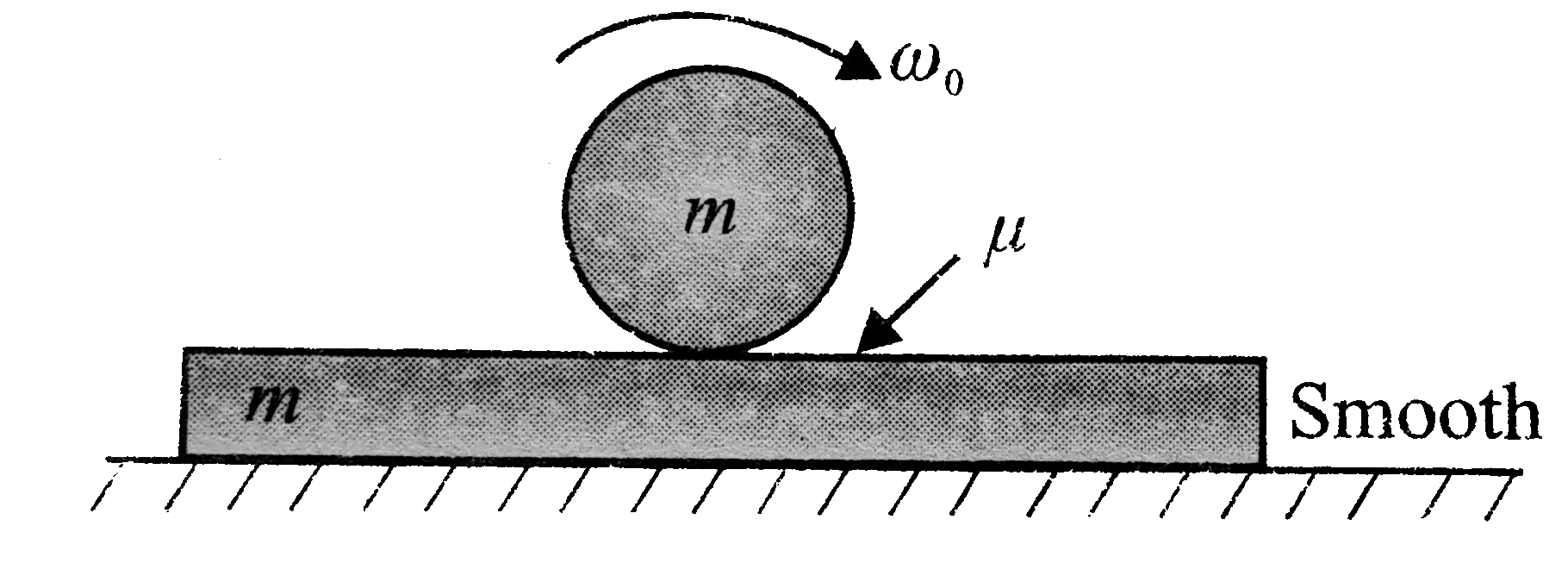
Find the velocity of the sphere after the pure rolling startsA2ω0r9Bω0r9Cω03D2ω0r3 - Question 3 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μg
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionA plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank
 View Solution
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.View Solution

