For the L-shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point A becomes equal to p02? (p0 is the atmospheric pressure)

g
g2+p02ρH
p02ρH
ρ02ρH+g
The correct Answer is:C
pA=ρaH−ρgH=pB
Here pA=p02 and pB=p0
∴−p02=ρgH=ρaH
⇒pH(a−g)=p02⇒a=p02ρH+g
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Figure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.

View SolutionAir is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (=T0) but pressure (P1) is slightly larger than the atmospheric pressure (P0). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P0. The jar is now allowed to slowly warm up to its original temperature T0. At this time the pressure of the air inside is P2(P0<P2<P1). Assume air to be an ideal gas. Calculate the ratio of specific heats (=γ) for the air, in terms of P0,P1 and P2.
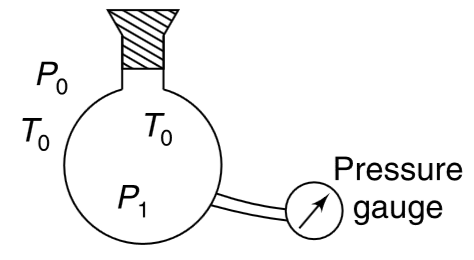
View Solution
Knowledge Check
In the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
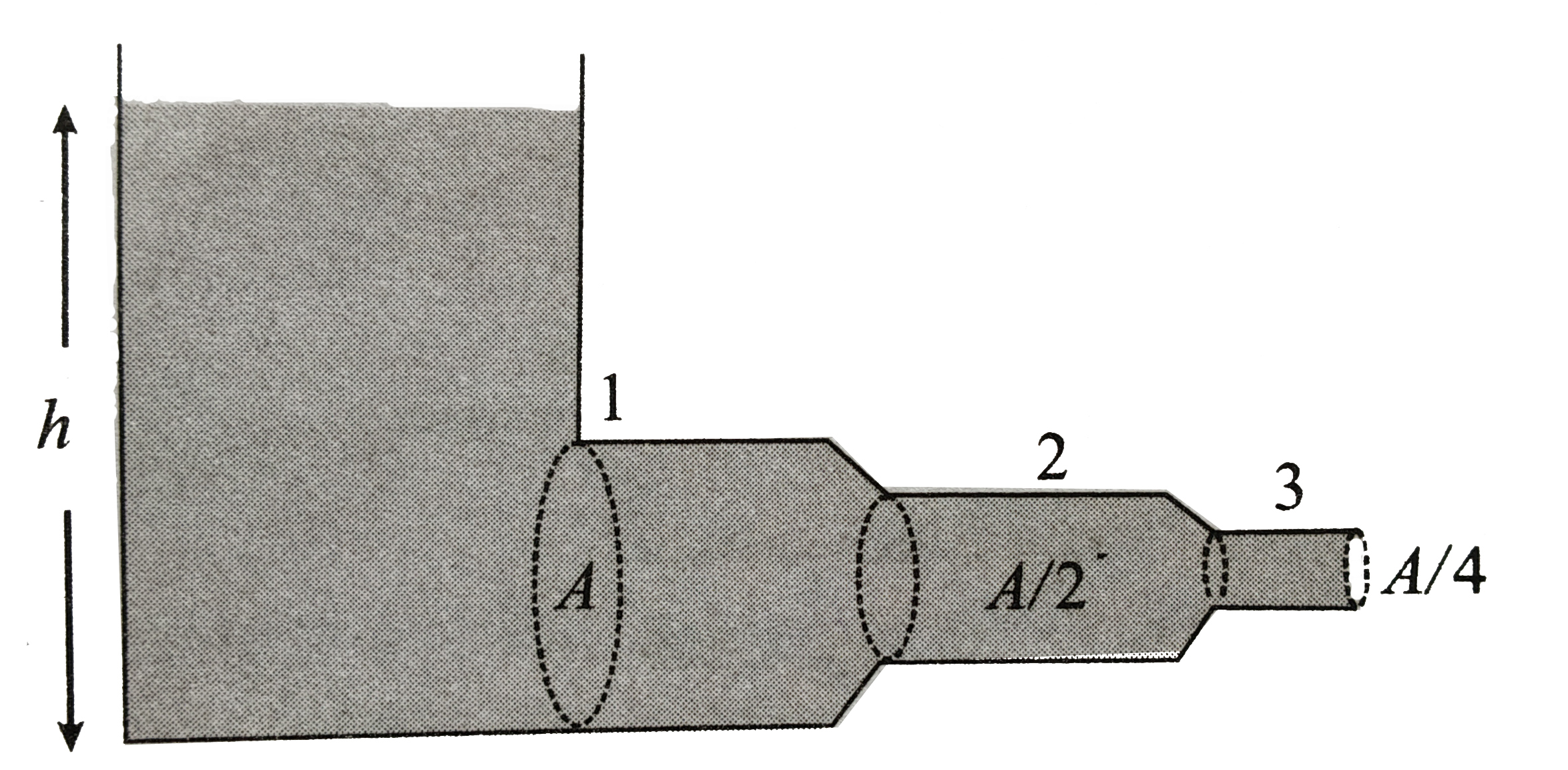 A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4
A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4Figure shows a siphon. Choose the wrong statement.

(p0 = atmospheric pressure)ASiphon works when h>0BPressure at point 2 inside the tube is p2=p0−ρghCPressure at point 3 is p0DNone of the aboveThe density of water at the surface of ocean is ρ . If the bulk modulus of water is B, then the density of ocean water at depth, when the pressure is αp0 and p0 is the atmospheric pressure is
ApBB−(α−1)p0BpBB+(α−1)p0CpBB−αp0DpBB+αp0
A cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
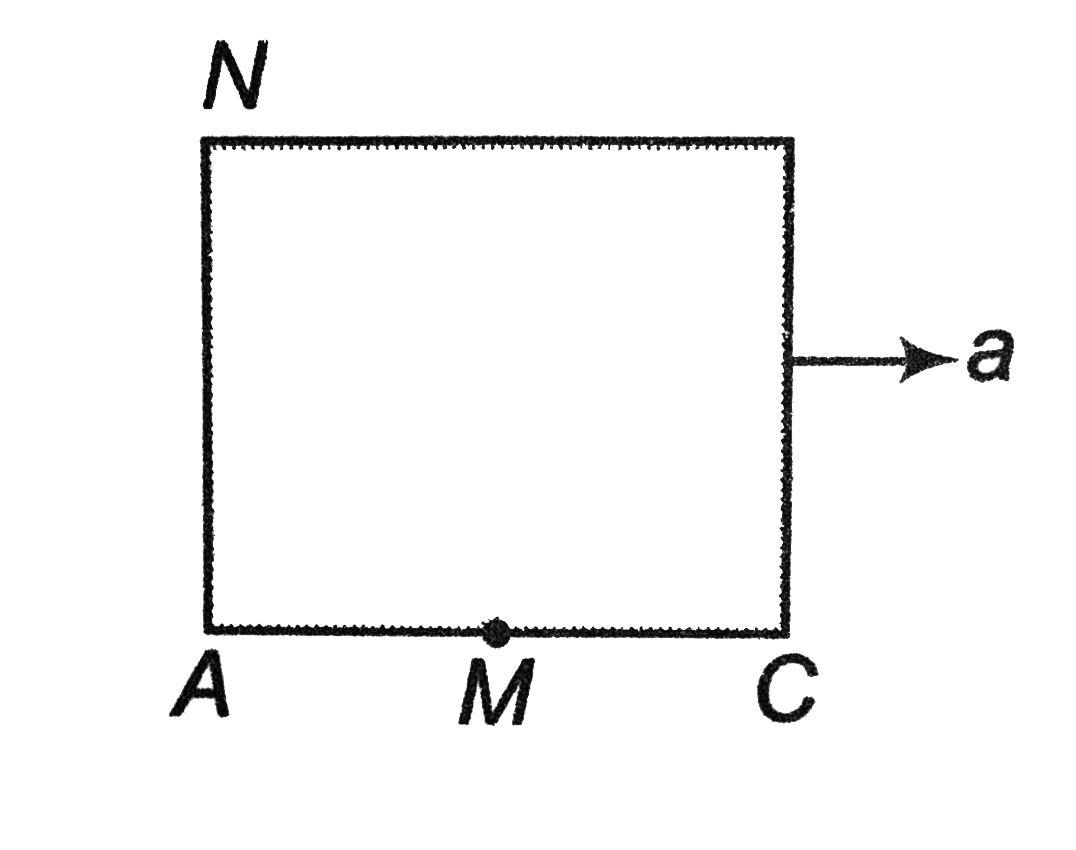 .
.
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is cthe cross-sectional are of the cylinder. at this time, the temperature of the gas has become.

View SolutionThe minimum horizontal acceleration of the container IS a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
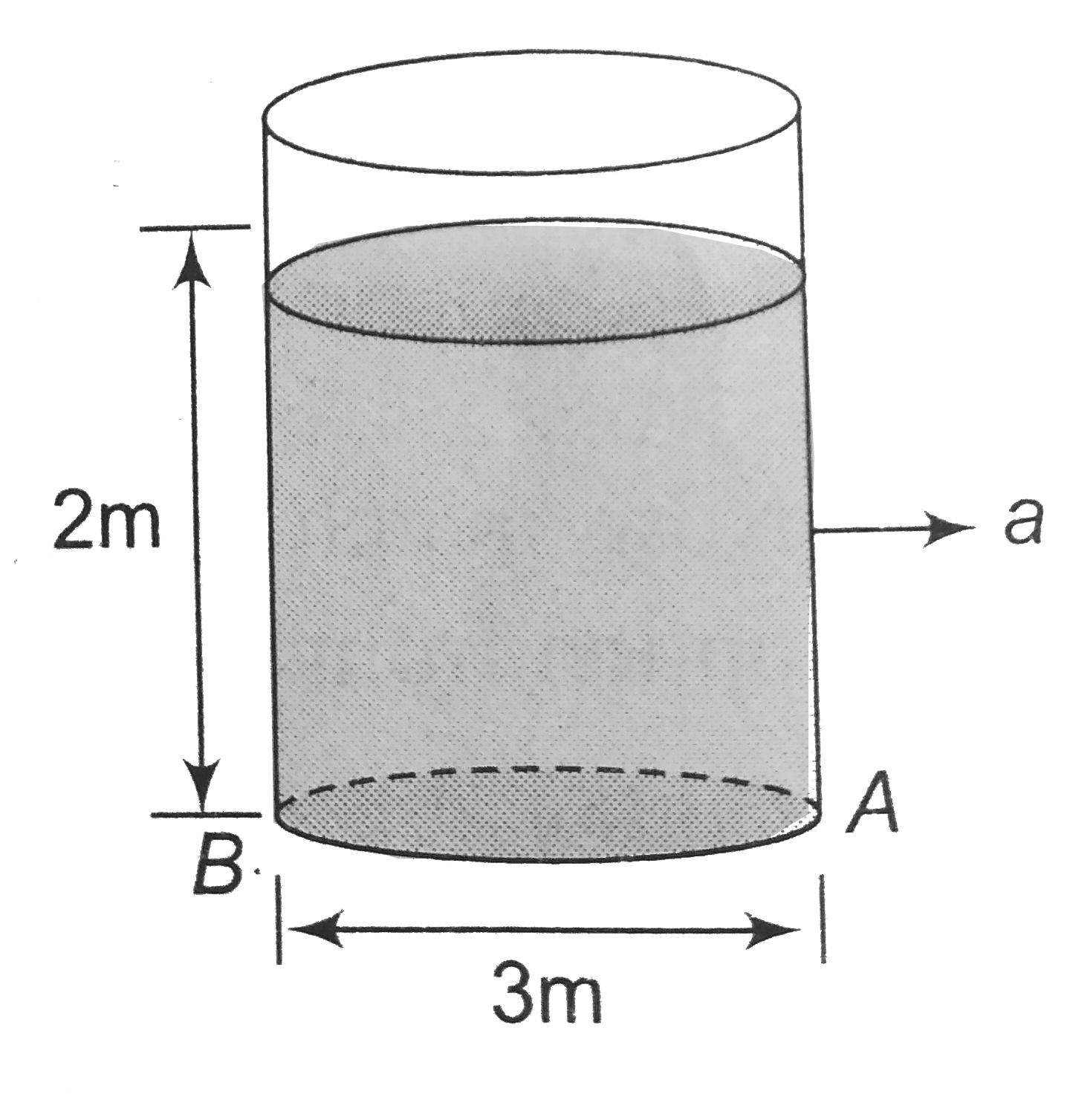
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
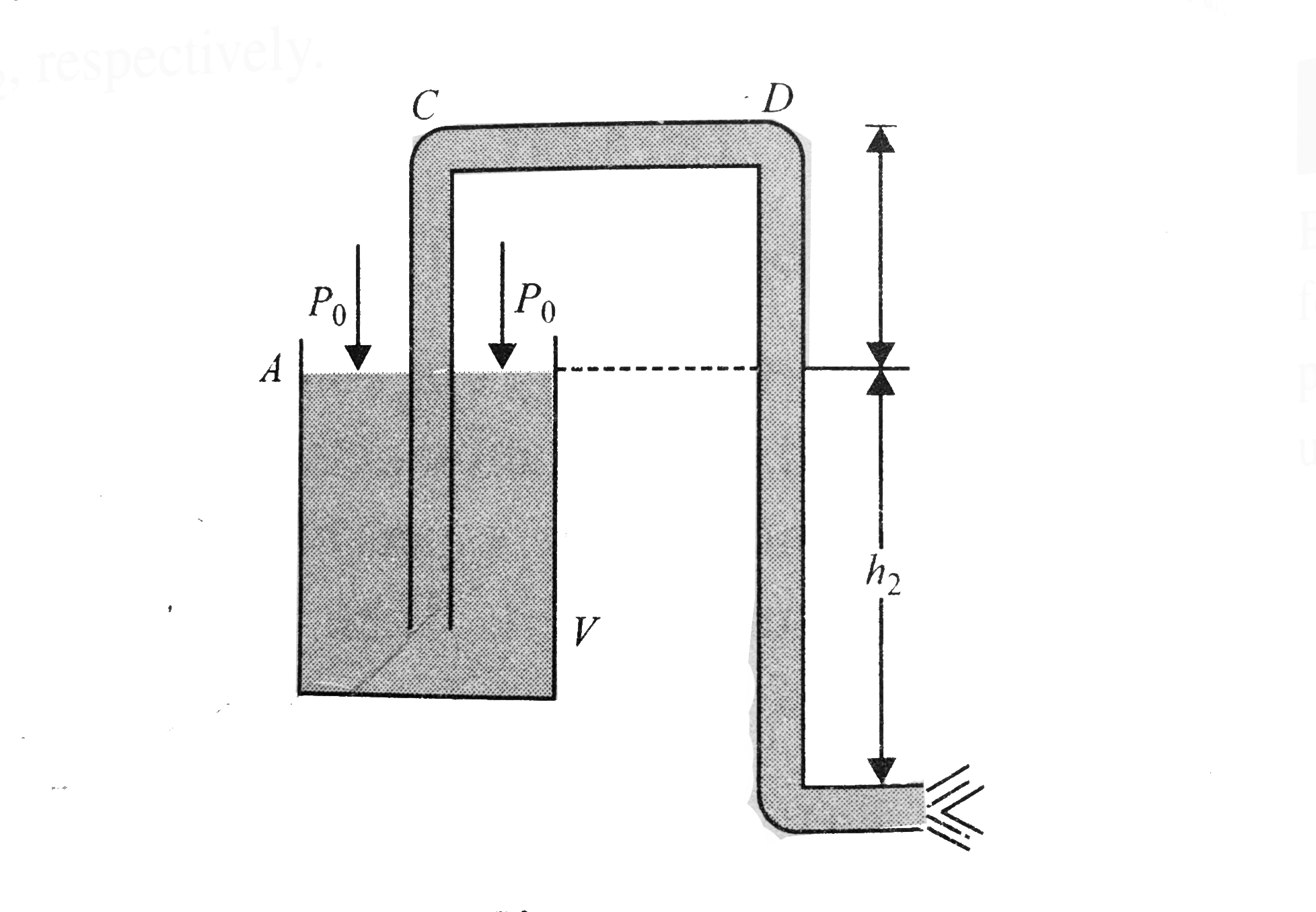
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will be
View Solution
