Two point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
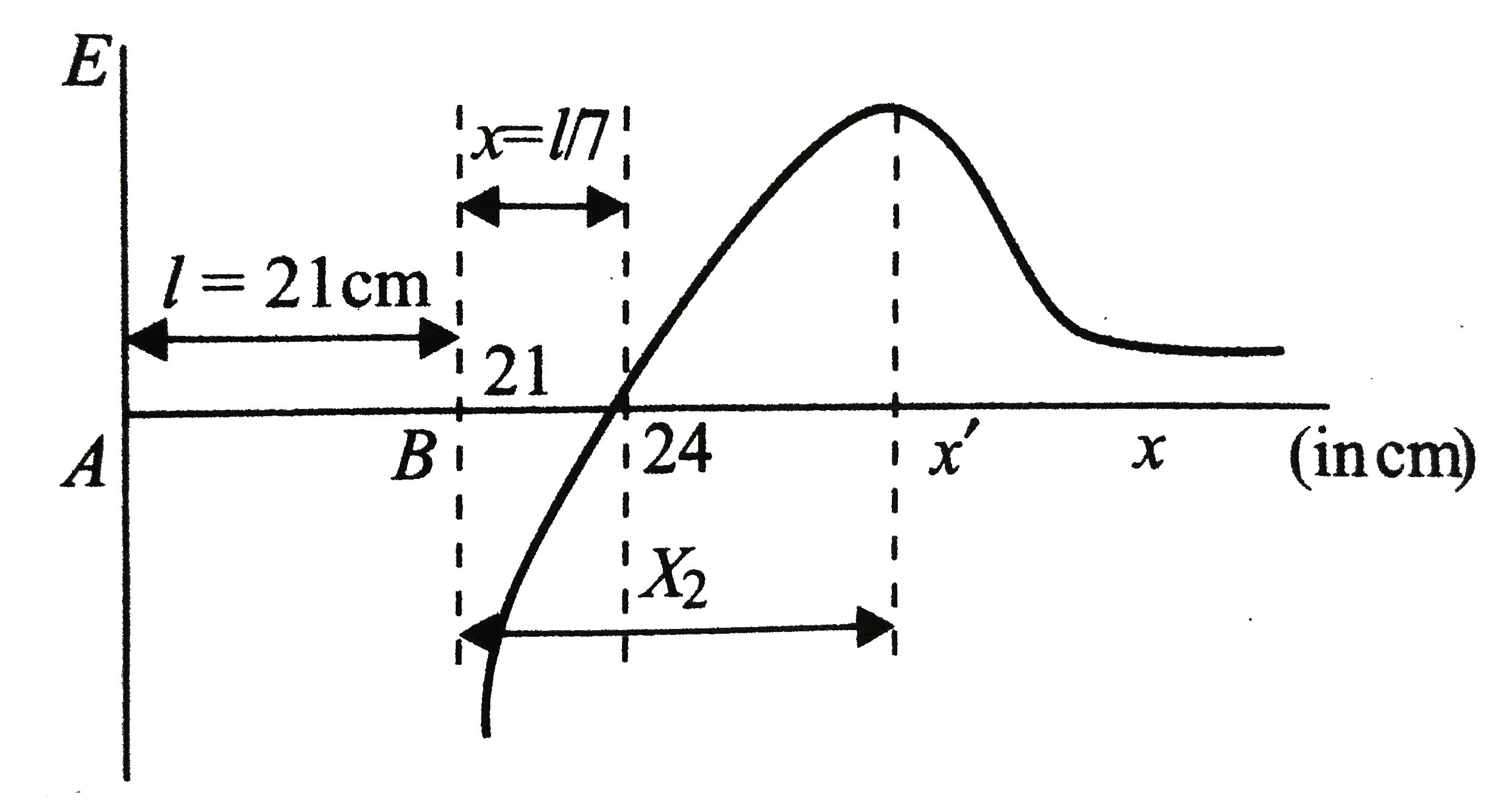
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
l(Q1/Q2)1/3+1
l(Q1/Q2)1/3−1
l(Q2/Q1)1/3+1
l(Q2/Q1)1/3−1
The correct Answer is:B
Electric field at (2) tends to −∞, hence the charge at (2) should be negative. There is a neutral point to the right of charges. This is possible onlu when the charge at (1) should be positive. Hence Q1 is positive and Q2 is negative. At netural point, →E1=→E2.
14πε0Q1(a+l)2=14πε0Q2a2 or Q1Q2=(a+la)2
Electric field at any position to the right of charges is
E=E1−E2=14πε0Q1(l+x)2−14πε0Q2x2
For the maximum value of E,
dEdx=0orddx[14πε0Q(l+x)2−14πε0Q2x2]=0
Q1−2(l+x)3−Q2−2x3=0
or Q1(l+x)3=Q2x3 or (l+xx)3=Q1Q2
or, l+xx=(Q1Q2)1/3 or lx=(Q1Q2)1/3−1
or x=l(Q1Q2)1/3−1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type20videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK19videos
COMMUNICATION SYSTEM
- BOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK40videos
Current Electricity
Similar Questions
Two point charge Qa and Qb are positional at point A and B. The field strenght to the right of charge Qb on the line that passes therough the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincedes with the positive direction of the x-axis. The distance between the charges is l=21cm.

(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
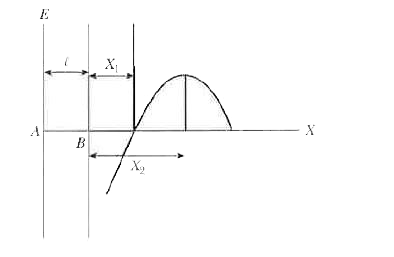
(c ) Find the coordinate x of the point where the field strenght is maximum.View SolutionTwo points like charges QA and QB are positioned at points a and B (see figure). The electric field strength to the right of charge QB on the line that passes through the two charges varies according to a law that is represented schematically in Figure below accompaanying the problem without employing a definite scale. Assume electric field to be positive if its direct ion coincides with (the positive direction on the x-axis. THe distance between the charges is l.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
A→r1√q1+→r2√q2√q1+√q2B→r1√q2+→r2√q1√q1+√q2C→r1√q2+→r2√q1√q1+q2D→r1√q1+→r2√q2√q1+q2 - Question 2 - Select One
Two fixed charges 4Q (positive) and Q (negative) are located at A and Bthe distance AB being 3m
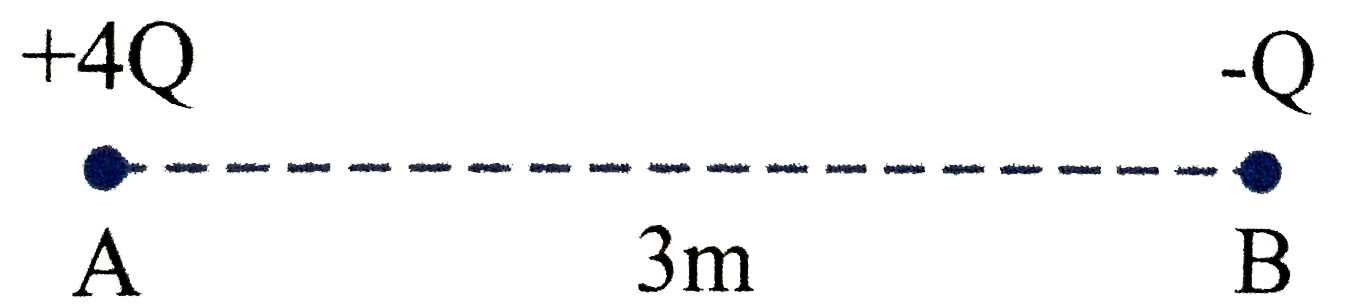 AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations.
AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations. - Question 3 - Select One
Two equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
Aexecute simple harmonic motion about the originBmove to the origin and remain at restCmove to infinityDsame as at point 25 cm aways form the surface
Two point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
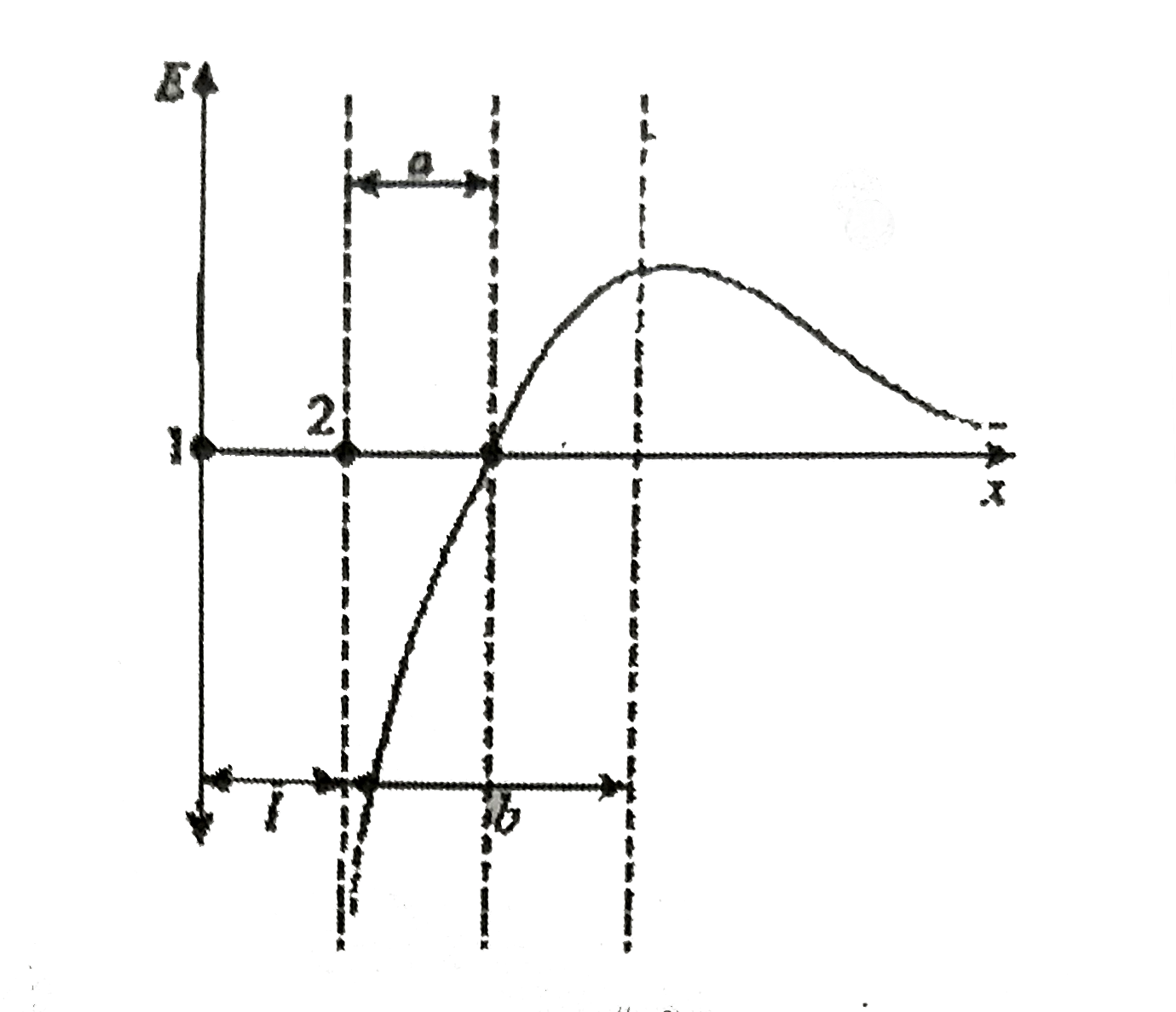
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥ ⎥ ⎥⎦View SolutionTwo point-like charges a and b whose strengths are equal in absolute value are positioned at a certain distance from each other. Assuming the field strength is positive in the direction coinciding with the positive direction of the r axis, determine the signs of the charges for each distribution of the field strength between the charges shown in Figures (a),(b),(c),and(d).
View SolutionTwo equal like charges are positioned at a certain distance from each other. How do the electric field strength and the potential vary along the axis that passes through the midpoint of the distance between the charges at right angles to the line connecting the charges?
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo charge +q and −q are kept apart.then at any point on the right beisector of line joining the two charges
View Solution

