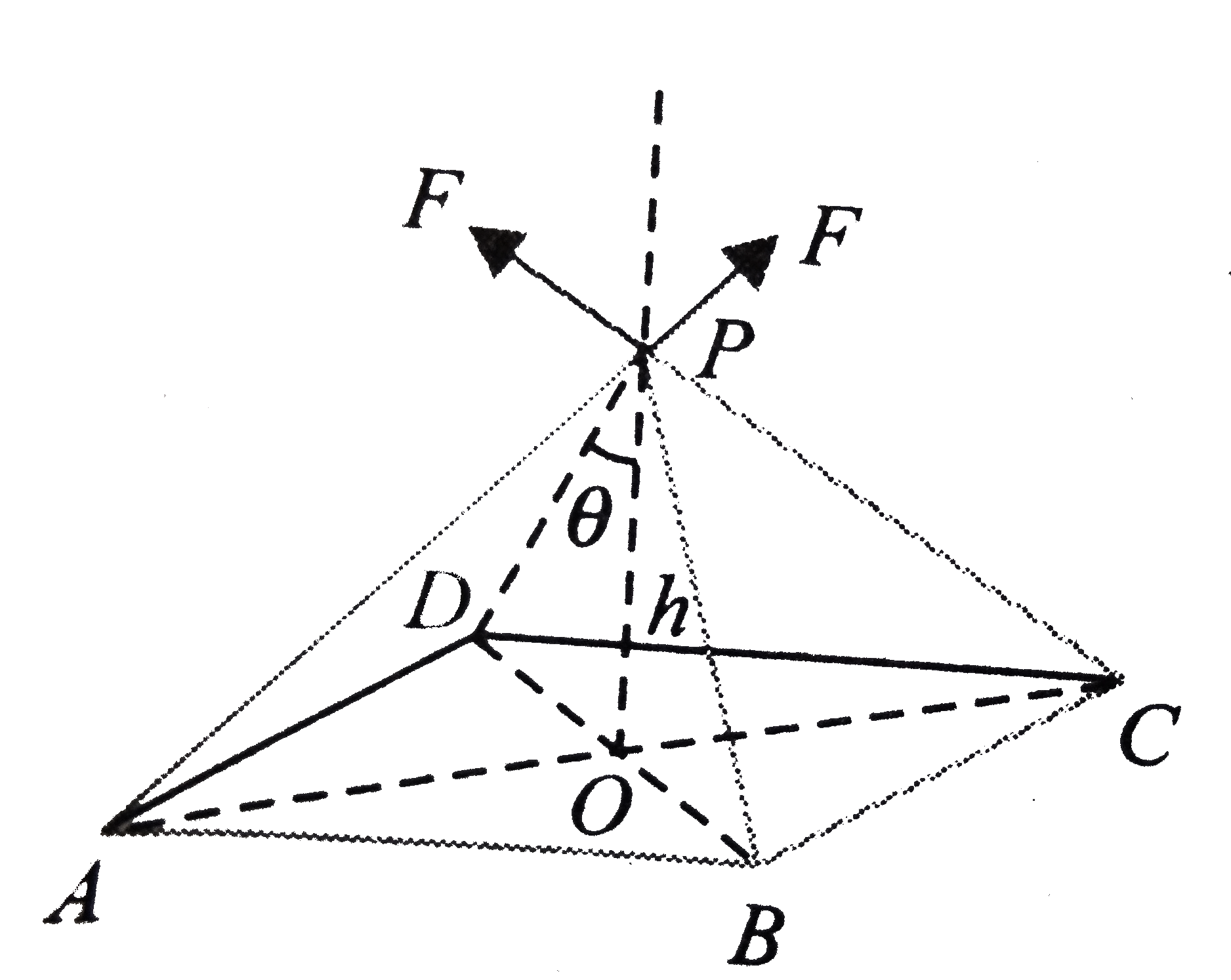
Four equal positive charges, each of value Q, are arranged at the four corners of a square of diagonal 2a. A small body of mass m carrying a unit positive charge is placed at height h above the center of the square.
What should be the value of Q in order taht this vody may be in equilibrium?

A

$π ε_{0} \frac{m g}{2 h} {(h^{2} + 2 a^{2})}^{3 / 2}$

B

$π ε_{0} \frac{m g}{2 h} {(h^{2} + a^{2})}^{3 / 2}$

C

$π ε_{0} \frac{2 m g}{2 h} {(h^{2} + 2 a^{2})}^{3 / 2}$

D

$π ε_{0} \frac{m g}{2 h} {(h^{2} - 2 a^{2})}^{3 / 2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$O A = O B = O C = O D = a$
The magnitude of the electric force due to each charge is
$\frac{1}{4 π ε_{0}} \frac{Q}{a^{2} + h^{2}}$
The components of the force perpendicular to OP sum up to zero because of the smmetrical distribution of charge about OP. Hence, the resultalant force at P is upward along OP. The magnitude of the force is given by
$F_{u p} = 4 \times \frac{1}{4 π ε_{0}} \frac{Q}{h^{2} + a^{2}} cos θ$
$\frac{Q}{π ε_{0} (h^{2} + a^{2})} \frac{h}{\sqrt{h^{2} + a^{2}}} = \frac{Q h}{π ε_{0} {(h^{2} + a^{2})}^{3 / 2}}$
$F_{down} = w e i g h t = m g$
For equilbrium, $m g = \frac{Q h}{π ε_{0} {(h^{2} + a^{2})}^{3 / 2}}$
or $Q = π ε_{0} \frac{m g}{h} {(h^{2} + a^{2})}^{3 / 2}$
yes this is a stabel equilibrium as it will regain its position if displaced a little.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three point charges each of value $+ q$ are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value $- q$ coulomb placed at the centre of the square?
A $(\frac{1}{4 π ε_{0}}) {(\frac{q}{a})}^{2}$
B $(\frac{1}{2 π ε_{0}}) {(\frac{2 q}{a})}^{2}$
C $(\frac{1}{2 π ε_{0}}) {(\frac{q}{a})}^{2}$
D $(\frac{1}{4 π ε_{0}}) {(\frac{2 q}{a})}^{2}$
Question 2 - Select One
Four equal charges $Q$ are placed at the four corners of a square of each side is 'a'. Work done in removing a charge $- Q$ from its centre to infinity is
Azero
B $\frac{\sqrt{2} q^{2}}{π \in_{0} a}$
C $\frac{\sqrt{2} q}{π \in_{0} a}$
D $\frac{q^{2}}{π \in_{0} a}$
Question 3 - Select One
Four equal charges $Q$ are placed at the four corners of a square of each side is 'a'. Work done in removing a charge $- Q$ from its centre to infinity is
A $0$
B $\frac{\sqrt{2} Q^{2}}{4 π ε_{0} a}$
C $\frac{\sqrt{2} Q^{2}}{π ε_{0} a}$
D $\frac{Q^{2}}{2 π ε_{0} a}$

CENGAGE PHYSICS-COULOMB LAW AND ELECTRIC FIELD-Comprehension

Home
Ask Doubt
Profile