A simple pendulum of mass m charged negatively to q coulomb oscillates with a time period T in a down ward electric field E such that mg>qE.

At equilibrium of he bob, the change in tension in the string will be (assuming rest condition)
mg
qE
2qE
qE/2
The correct Answer is:B
T=2π√l(mg−qE)/m
T'=2π√lg
or T'<T
Obviously change in tension is qE. Tension will increase by qE.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
A simple pendulum has a bob of mass m which carries a charge q on it. Length of the pendulum is L. There is a uniform electric field E in the region. Calculate the time period of small oscillations for the pendulum about its equilibrium position in following cases:
(i). E is vertically down having magnitude E=mgq
(ii). E is vertically up having magnitude E=2mgq
(iii). E is horizontal having magnitude E=mgq
(iv). E has magnitude of E=q and is directed upward making an angle 45∘ with the horizontal
View SolutionThe simple pendulum of the previous problem is placed in uniform electric field E, directed horizontally. Find the angle made by string with vertical in equilibrium and tension in the string . Now the ball is slightly displaced and it exceutes simple harmonic motion, find its time period of oscillation.
View Solution
Knowledge Check
A simple pendulum of mass m charged negatively to q coulomb oscillates with a time period T in a down ward electric field E such that mg>qE.

At equilibrium of he bob, the change in tension in the string will be (assuming rest condition)AmgBqEC2qEDqE/2A simple pendulum of mass m charged negatively to q coulomb oscillates with a timeperiod T in a down ward electric field E such that mggtqE..

If the electric field is withdrawn, the new time periodA=TB>TC<TDany of the above three is possibleA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
AmgsinθBmgCqEsinθDqEcosθ
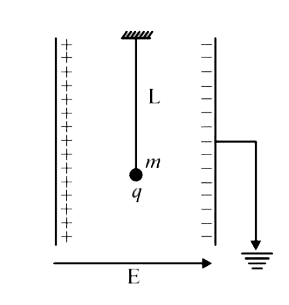
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionThe bob of a simple pendulum has mass 2g and a charge of 5.0μC. It is at rest in a uniform horizontal electric field of intensity 2000V/m. At equilibrium, the angle that the pendulum makes with the vertical is: (take g=10m/s2)
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionIf a simple pendulum has charge q and is oscillating in a uniform electric field E in the direction of acceleration due to gravity, then its frequency of oscillations
View Solution
