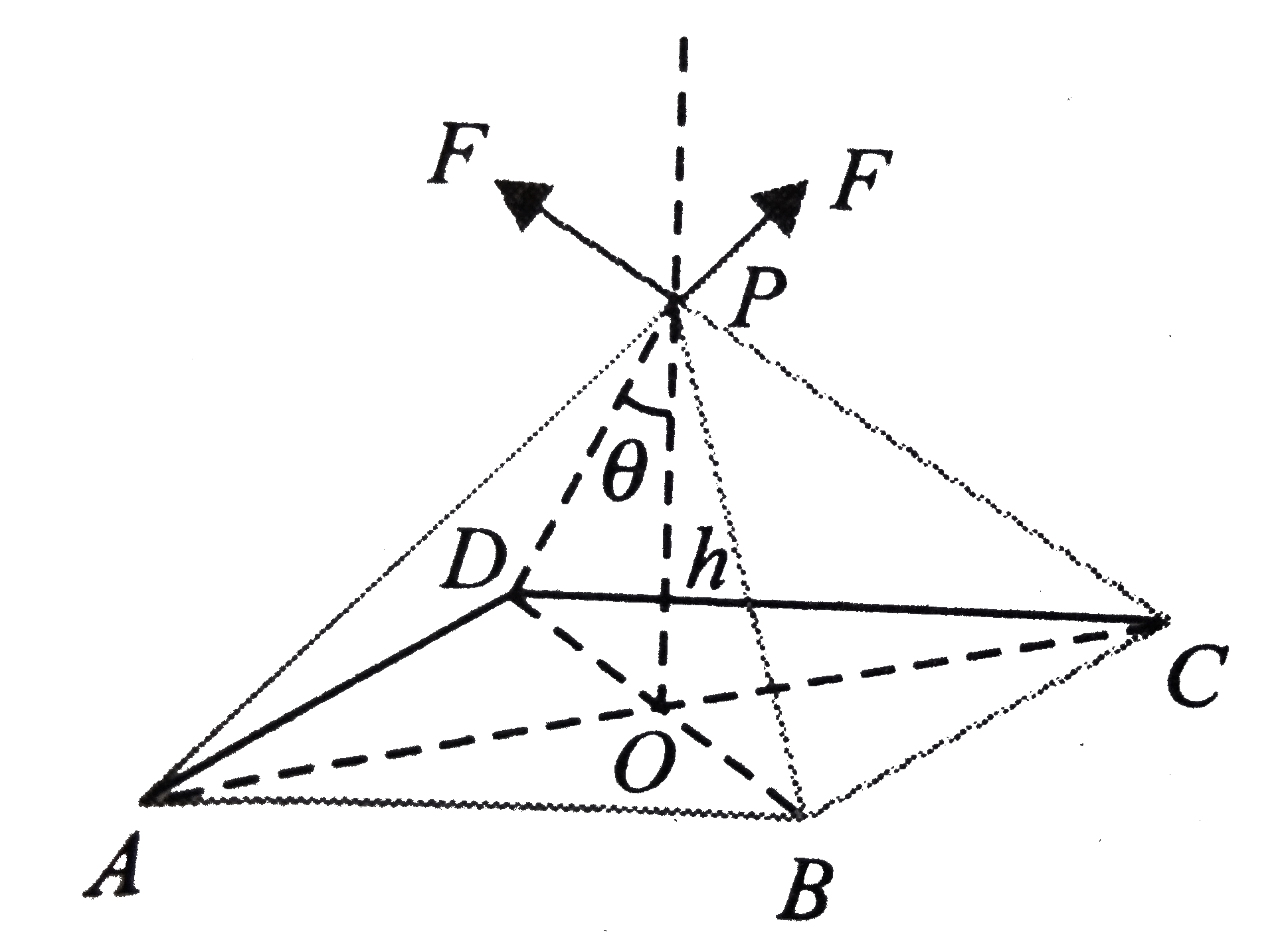
Four equal positive charges, each of value Q, are arranged at the four corners of a square of diagonal 2a. A small body of mass m carrying a unit positive charge is placed at height h above the center of the square.
What should be the value of Q in order that this body may be in equilibrium?
stable equilibrium
unstable equilibrium
neutral equilibrium
cannot be determined
The correct Answer is:A
OA=OB=OC=OD=a
The magnitude of the electric force due to each charge is
14πε0Qa2+h2
The components of the force perpendicular to OP sum up to zero because of the smmetrical distribution of charge about OP. Hence, the resultalant force at P is upward along OP. The magnitude of the force is given by
Fup=4×14πε0Qh2+a2cosθ
Qπε0(h2+a2)h√h2+a2=Qhπε0(h2+a2)3/2
Fdown=weight=mg
For equilbrium, mg=Qhπε0(h2+a2)3/2
or Q=πε0mgh(h2+a2)3/2
yes this is a stabel equilibrium as it will regain its position if displaced a little.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type20videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK19videos
COMMUNICATION SYSTEM
- BOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK40videos
Current Electricity
Similar Questions
Four small particles charged with equal positive charges Q each are arranged at the four corners of a horizontal square of side a. A unit positive charge mass m is placed at a point P, at a height h above the centre of the square. What should be the magnitude of charge Q in order that the unit charge remain in equilibrium
View SolutionFour equal point charges, each of magnitude +Q, are to be placed in equilibrium at the corners of a square. What should be the magnitude and sign of the point charge that should be placed at the center of the square to do this job?
View Solution
Knowledge Check
- Question 1 - Select One
Four equal positive charges, each of value Q, are arranged at the four corners of a square of diagonal 2a. A small body of mass m carrying a unit positive charge is placed at height h above the center of the square.
What should be the value of Q in order taht this vody may be in equilibrium?Aπε0mg2h(h2+2a2)3/2Bπε0mg2h(h2+a2)3/2Cπε02mg2h(h2+2a2)3/2Dπε0mg2h(h2−2a2)3/2 - Question 2 - Select One
Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2 - Question 3 - Select One
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2π∈0aC√2qπ∈0aDq2π∈0a
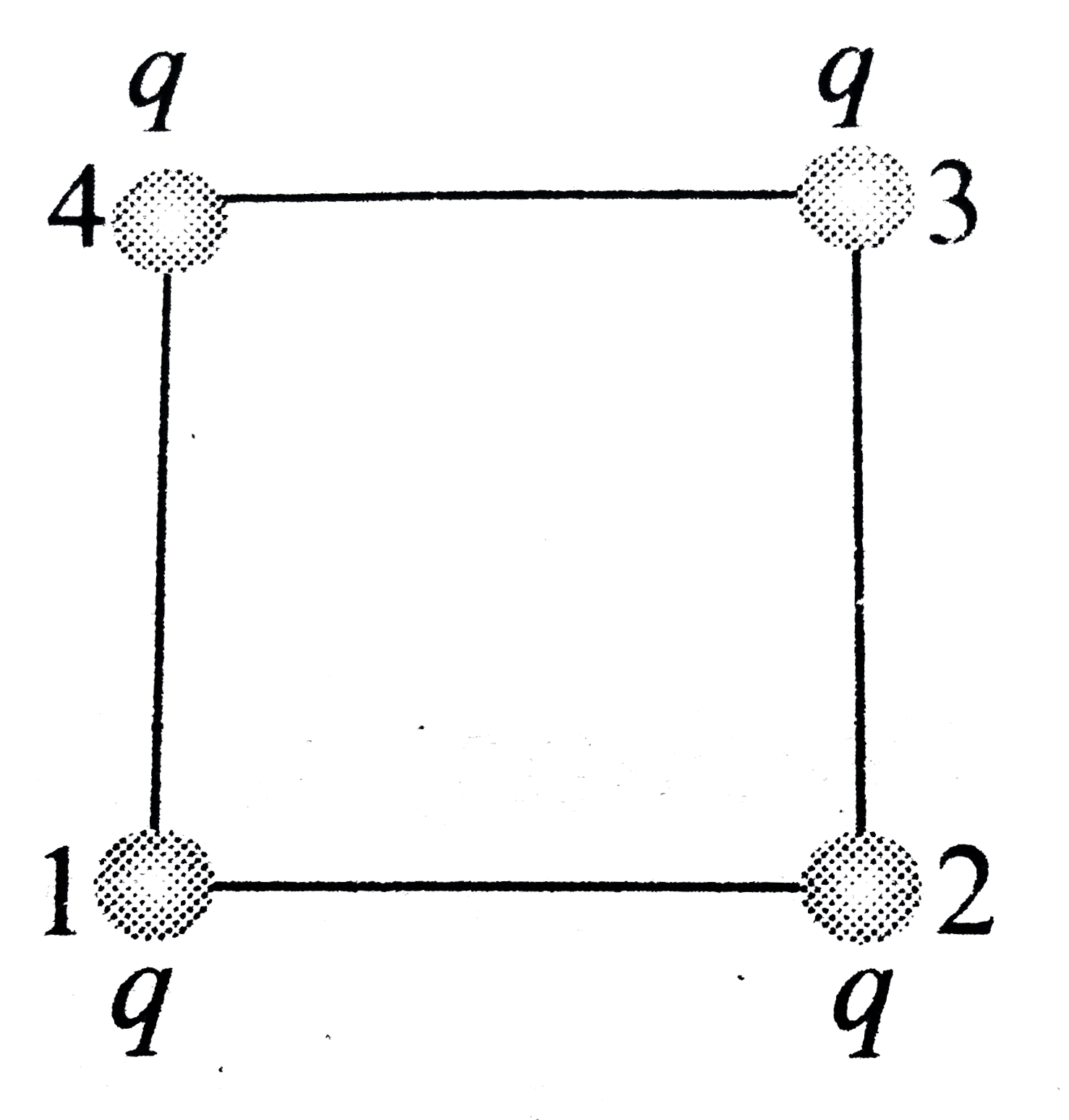
Four identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .View Solution
.View SolutionFour equal charges each 16μC are placed on four corners of a square of side 0.4m. Calculate force on q is zero, how are Q and q related ?
View SolutionFour equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionFour bodies of masses 2, 3, 5 and 8 kg are placed at the four corners of a square of side 2 m. The position of CM will be -
View Solution

