An infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where R<d and R>d.

zero
2λRε0
2λ√R2−y2ε0
λ√R2+y2ε0
The correct Answer is:C
c. Electric flux ∮S→E⋅→ds=q∈ε0
q∈ is the charge enclosed by the Gaussian surface, which in
the present case, is the surface of the given sphere. As shown,
length AB of line lies inside the sphere. In ΔOO'A,
R2=Y2+(O'A)2
∴O'A=√R2−y2
and AB=2√R2−y2
Charge on length AB s 2√R2−Y2×λ
Therefore, electric flux is
∮S→E⋅→ds=2λ√R2−y2ε0

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
A long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
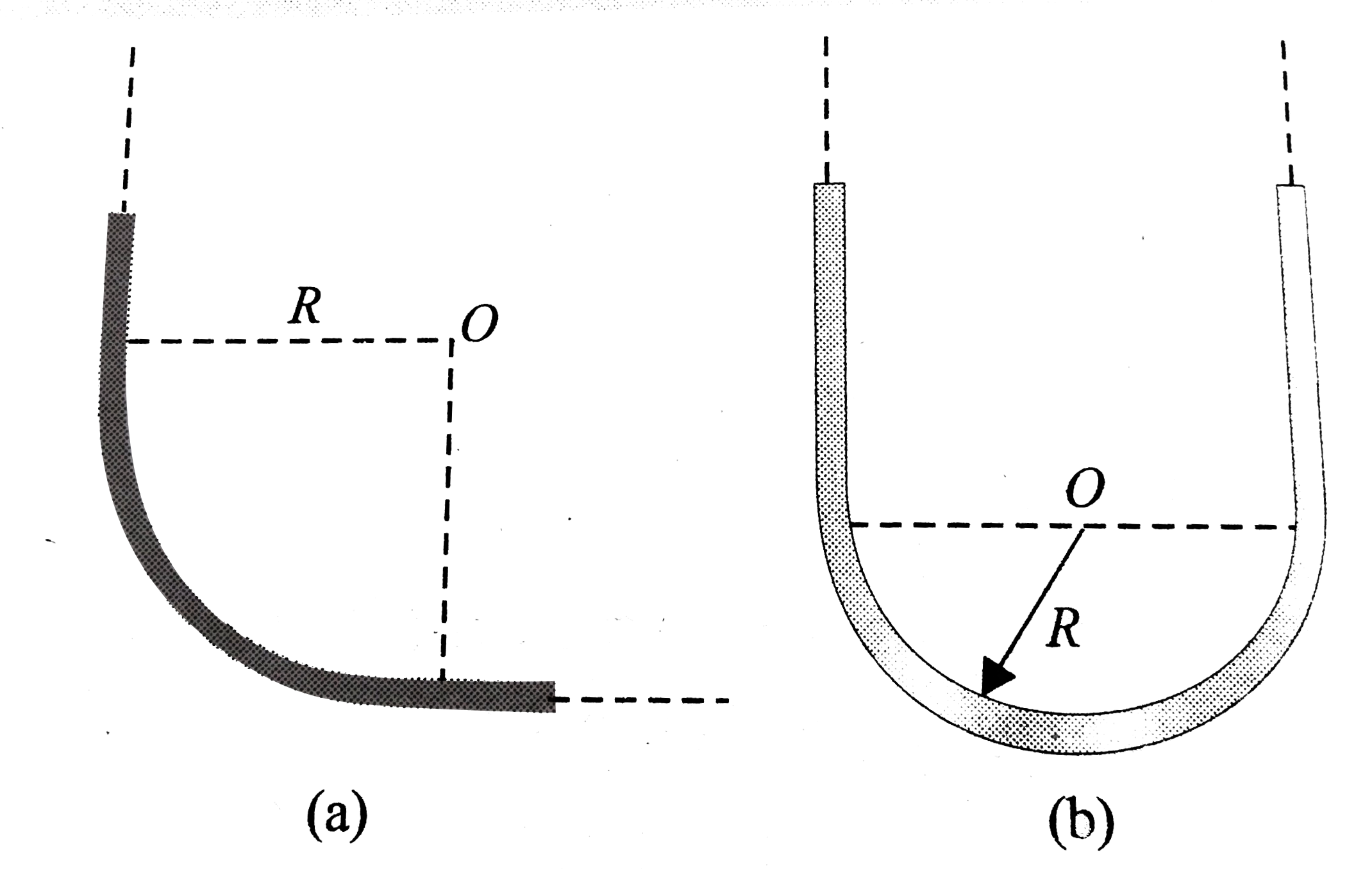 View Solution
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
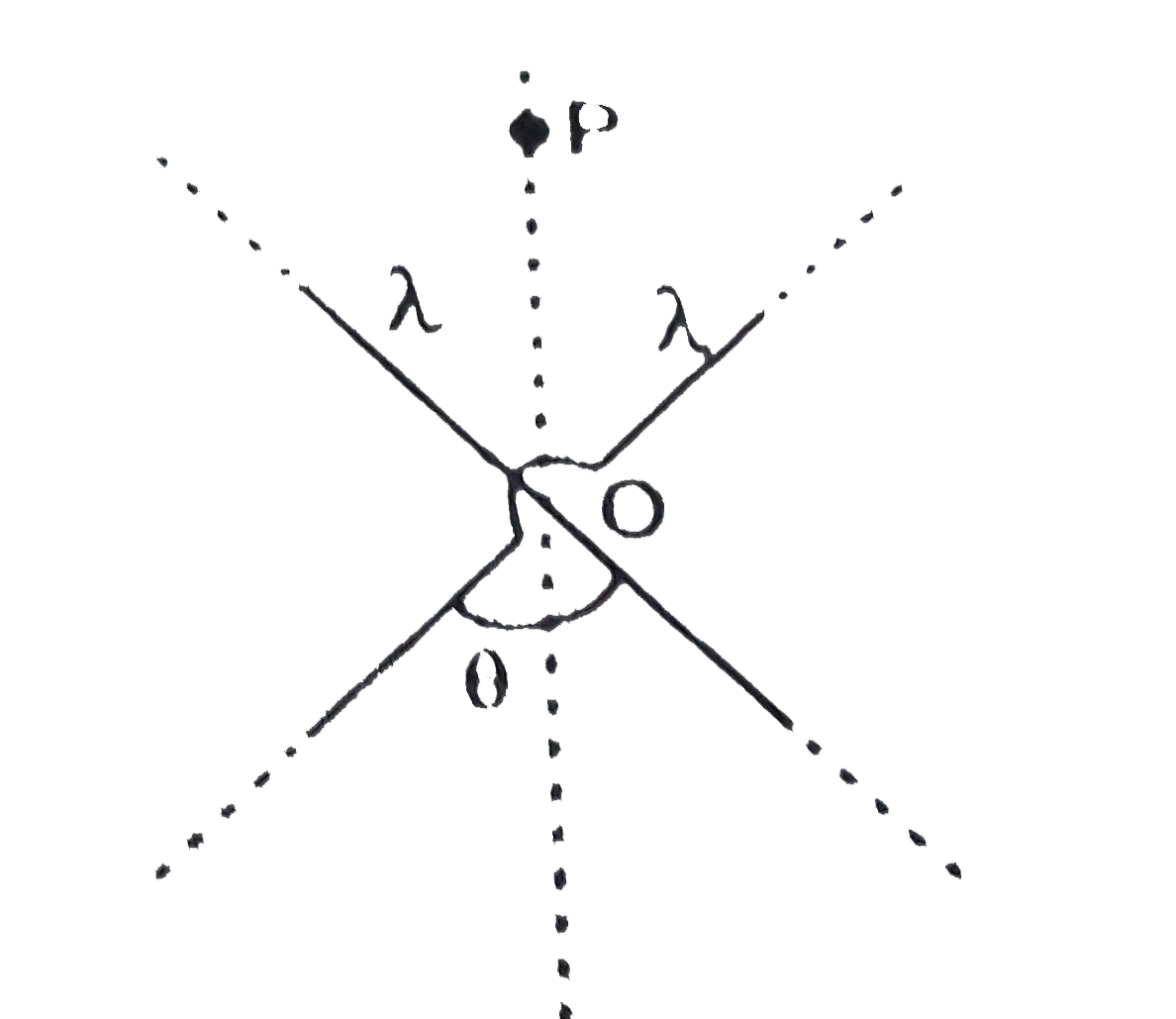
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The electric field at a distance r from a long wire having charge per unit length λ is
AE=2πε0λKr2BE=ε0λ2πKr2CE=λ2πε0KrDE=4πε0λKr2 - Question 2 - Select One
A uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is
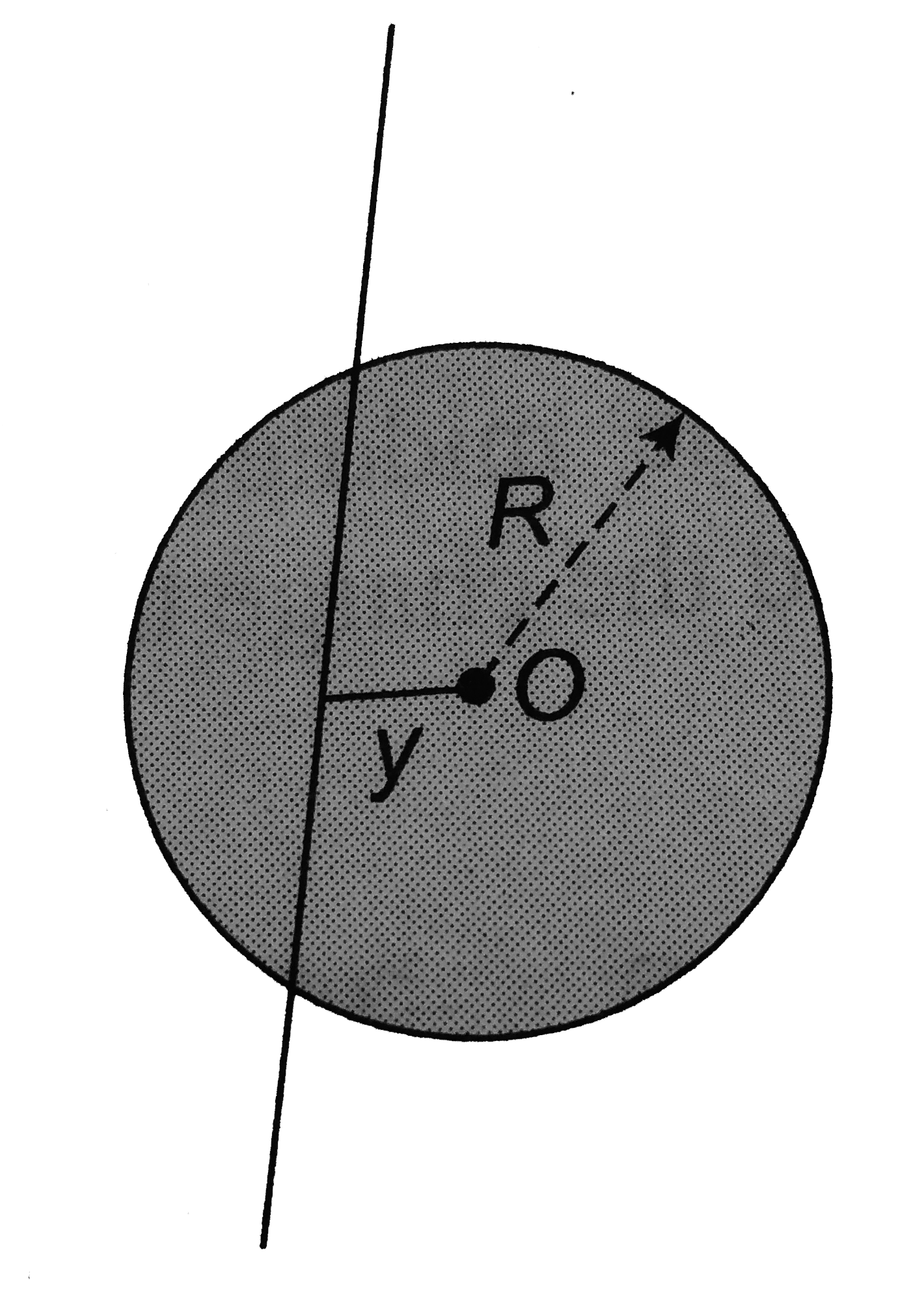 AzeroB2λRε0C2λ√R2−y2ε0Dλ√R2+y2ε0
AzeroB2λRε0C2λ√R2−y2ε0Dλ√R2+y2ε0 - Question 3 - Select One
Two infinite line charges each having uniform charges density lamdba .pass through the mid points of two pairs of opposite faces of a cube of edge L as shown in figure .The modulue of the total electric flux due to the both the line charges through the face
 ACDHGis λl2ε0BAEHDis λl3ε0CABCD is λl2ε0DCDHG is λl3ε0
ACDHGis λl2ε0BAEHDis λl3ε0CABCD is λl2ε0DCDHG is λl3ε0
A point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
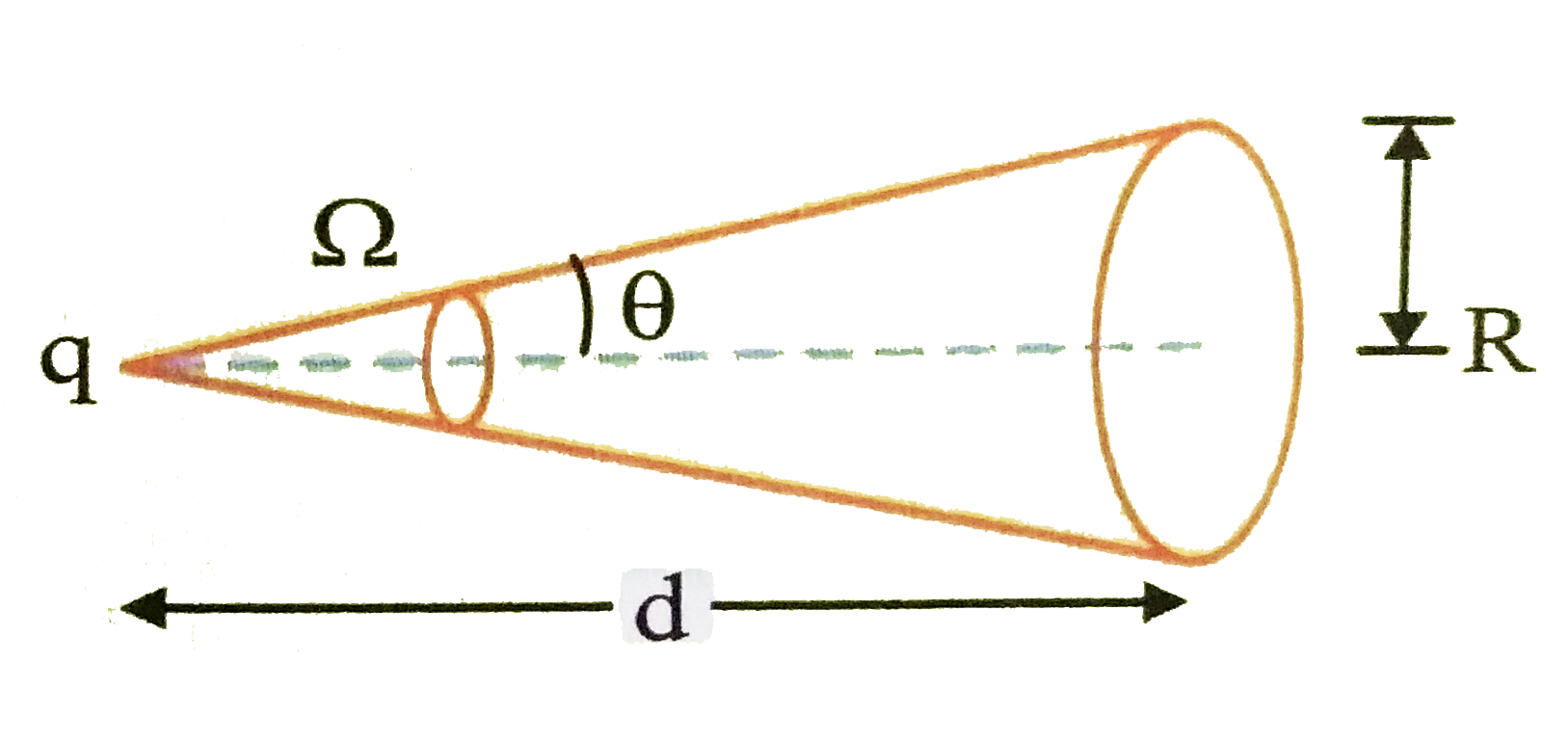 View Solution
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .
 View Solution
View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cyclinder. What will be the effect on the flux passing through curved surface if the portions of the line charge outside the cyclinder is removed
 View Solution
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
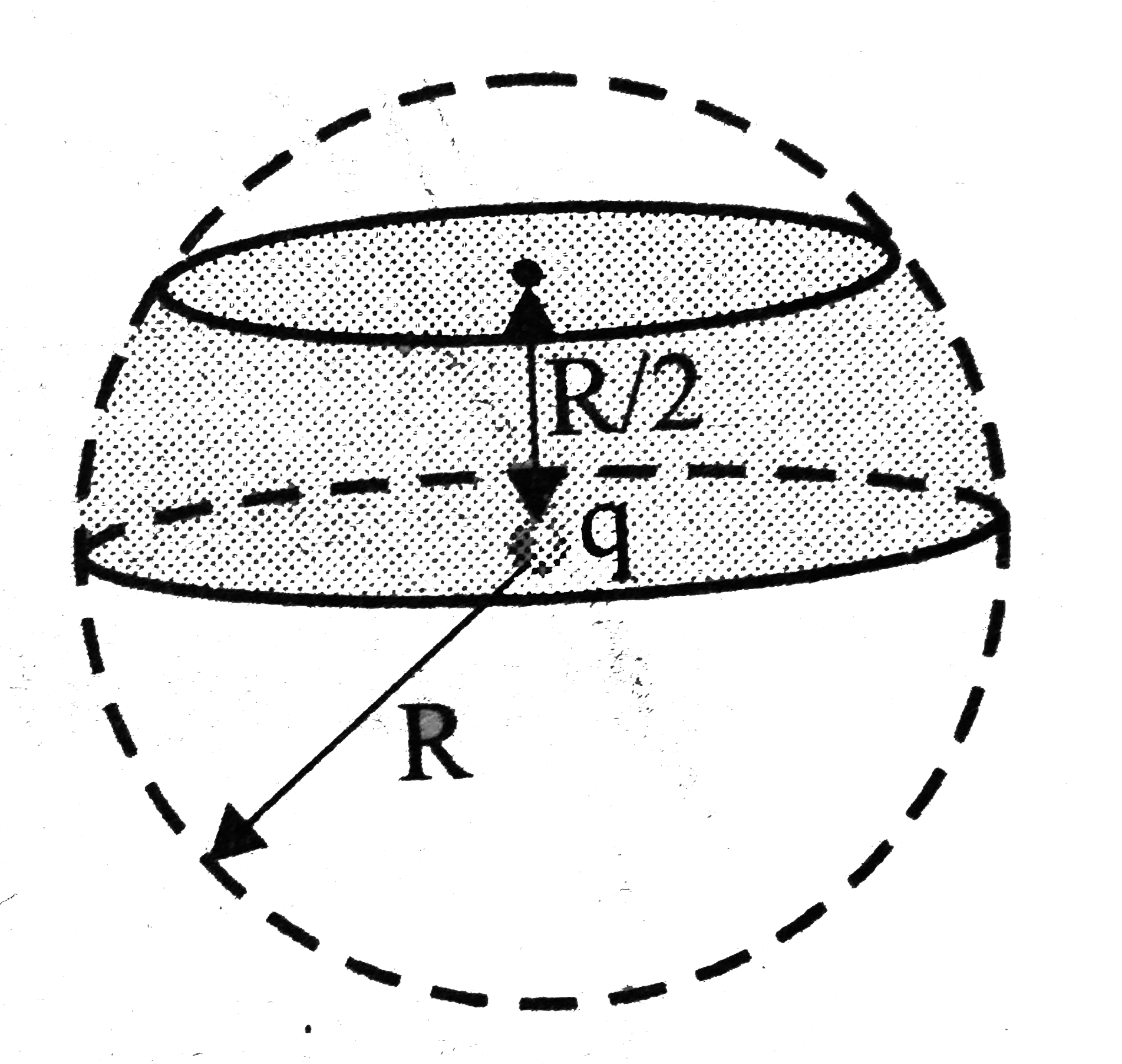 View Solution
View Solution

