One-fourth of a sphere of radius R is removed as shown in figure. An electric field E exists parallel to the xy plane . Find the flux through the remaining curved part.
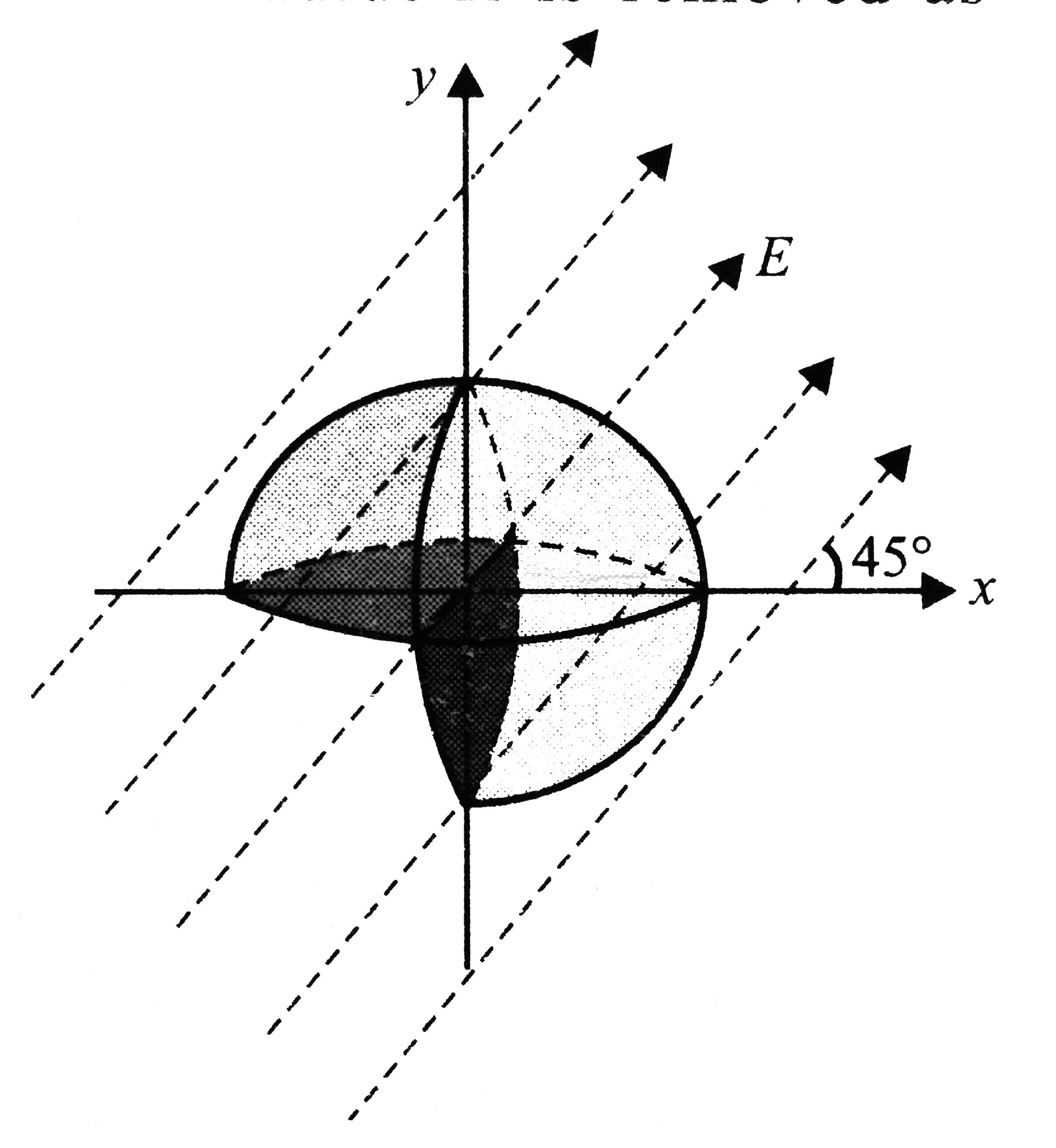
πR2R
√2πR2E
πR2E/√2
none of these
The correct Answer is:C
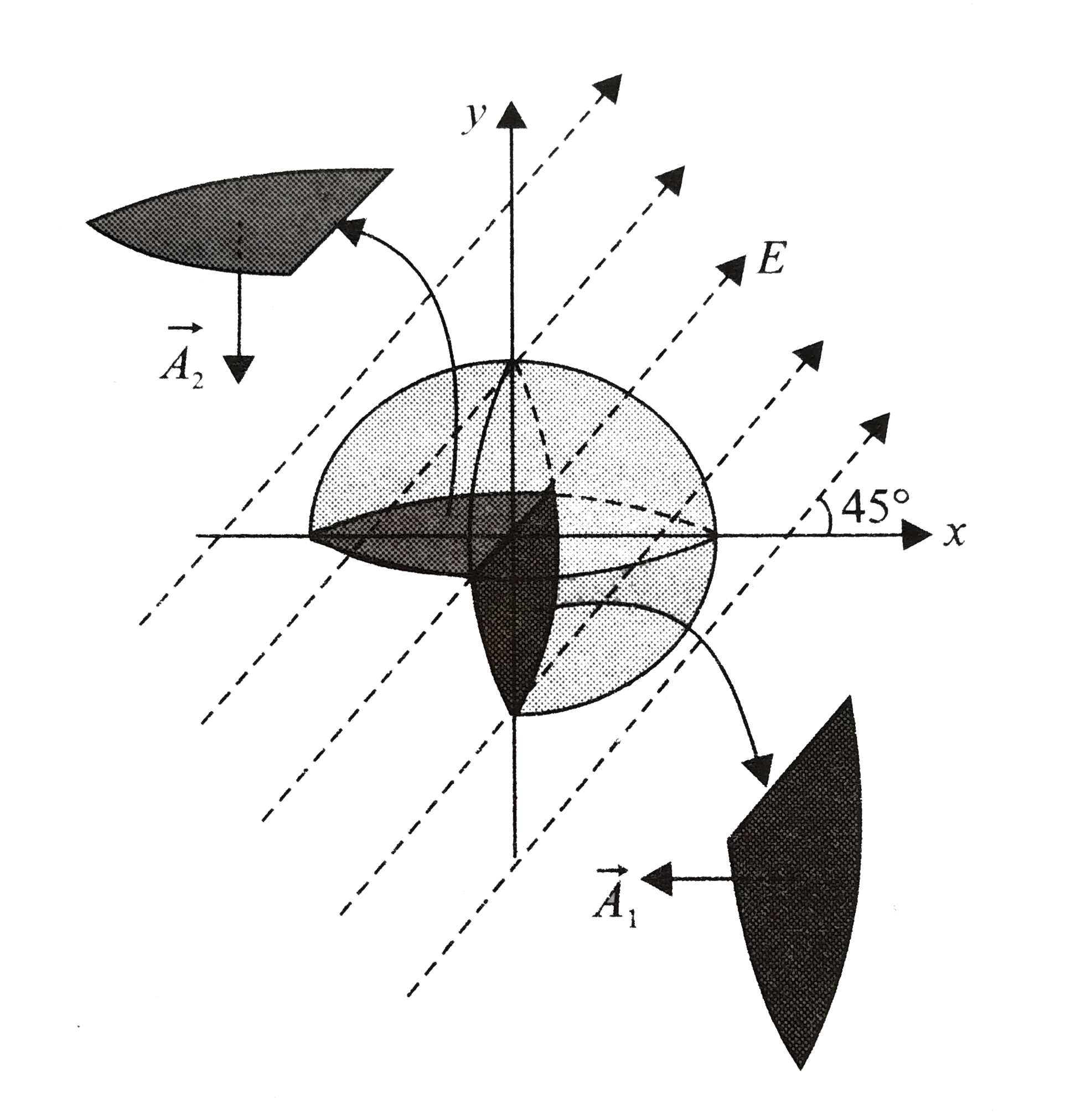
c. ϕpla∈+ϕcurve=0orϕpla∈=−ϕcurve
→A1=−πR22ˆi,→A2=−πR22ˆj
→E=Ecos45∘ˆi+Esin45∘ˆj
=E√2ˆi+E√2ˆj
ϕ=→E⋅(→A1+→A2)
=−E√2πR22−E√2πR22=−πR2E√2
This is the flux entering. So flux is πR2E√2.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Comprehension
Explore 36 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
A hollow half cylinder surface of radius R and length l is placed in a uniform electric field →E. Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface

View SolutionFron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.

View Solution
Knowledge Check
A hemispherical body of radius R is placed in a uniform electric field E. If the field E is parallel to the base of the hemisphere the flux linked with it is
A2πREB2πR2ECπR2EDzeroA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
A2πR2EBπR2/EC(πR2/πR)/EDZeroA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
AZeroB2πR2EC2πRLED(2πR2+2πRL)E
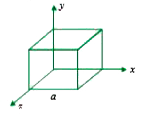
Given the electric field in the region →E=2ξ, find the net electric flux through the cube and enclosed by it.
View SolutionThe electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
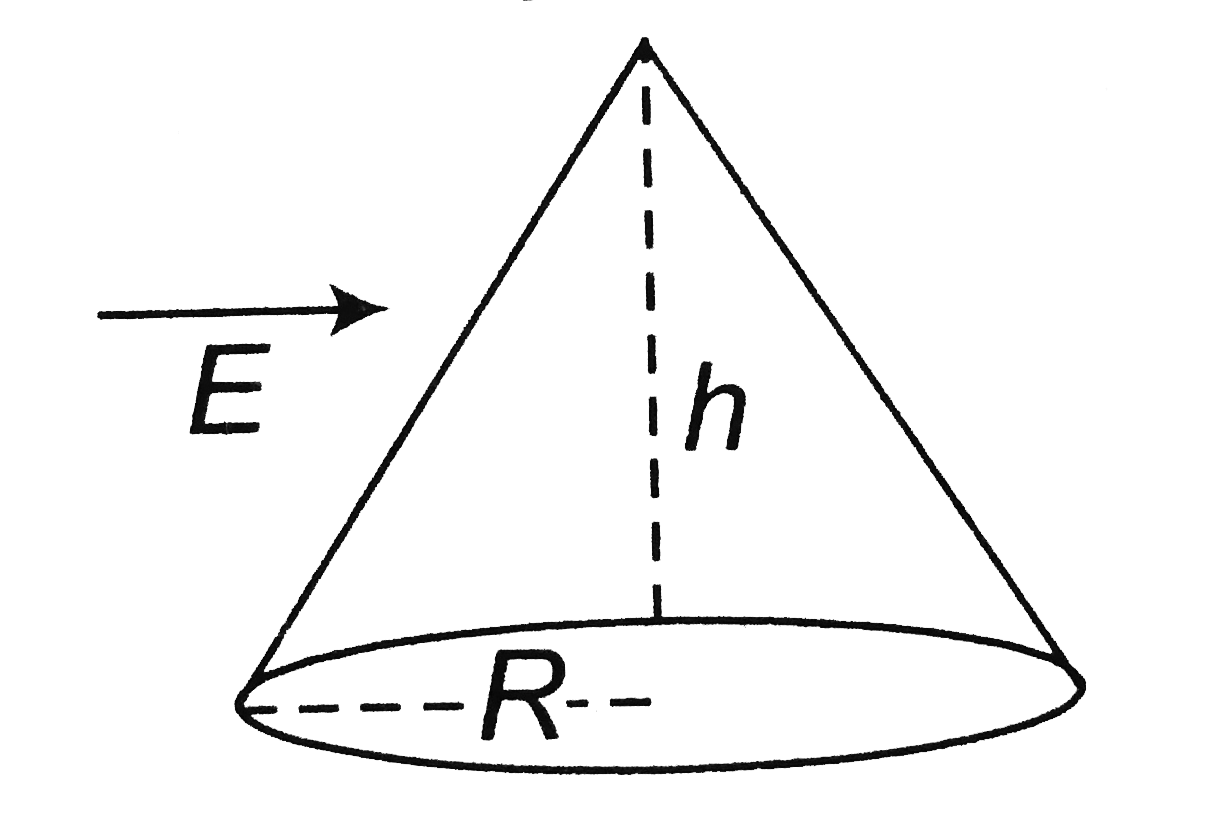
View SolutionA cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View Solution