In Fig. 27-38, two batteries with an emf ε=12.0V and an internal resistance r=0.500 Ω are connected in parallel across a resistance R. (a) For what value of R is the dissipation rate in the resistor a maximum? (b) What is that maximum? and (c) what is the total dissipation rate in the batteries? In terms of r, what are (d) the effective R (internal) resistance of the two-battery system and (e) the resistance R that is required to maximize the dissipation rate? This is a general result. 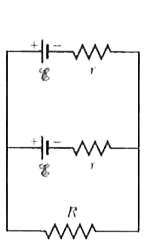
The correct Answer is:(a) 0.250Ω;(b)144W;(c)144W;(d)r/2;(e)r/2
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (More than One Correct Choice Type)
12 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
Two cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionA 24 V battery of internal resistance 4.0Ω is connected to a variable resistance. At what value of the current drawn from the battery is the rate of heat produced in the resistor maximum?
View Solution
Knowledge Check
Two cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
Ar/2BrC2rD0A battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
A2.0ohmB0.25ohmC1.0ohmD0.5ohm
A 24 V battery of internal resistance 4.0Ω is connected to a variable resistance. At what value of the current drawn from the battery is the rate of heat produced in the resistor maximum?
View SolutionA 24 V battery of internal resistance 4.0Ω is connected to a variable resistance. At what value of the current drawn from the battery is the rate of heat produced in the resistor maximum?
View SolutionA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View SolutionTwo batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View SolutionTwo batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View SolutionConsider the circuit shown in Figure . The terminal voltage of the 24.0 V battery is 21.2V. What are
(a) The internal resistance r of the battery and
(b) The resistance R of the circuit resistor ?

View Solution
