Charge over a nonconducting ring is distributed so that the linear charge density varies as $λ = λ_{0} sin θ$ . What is the direction of force on a charge $q_{0}$ placed at the center?

A

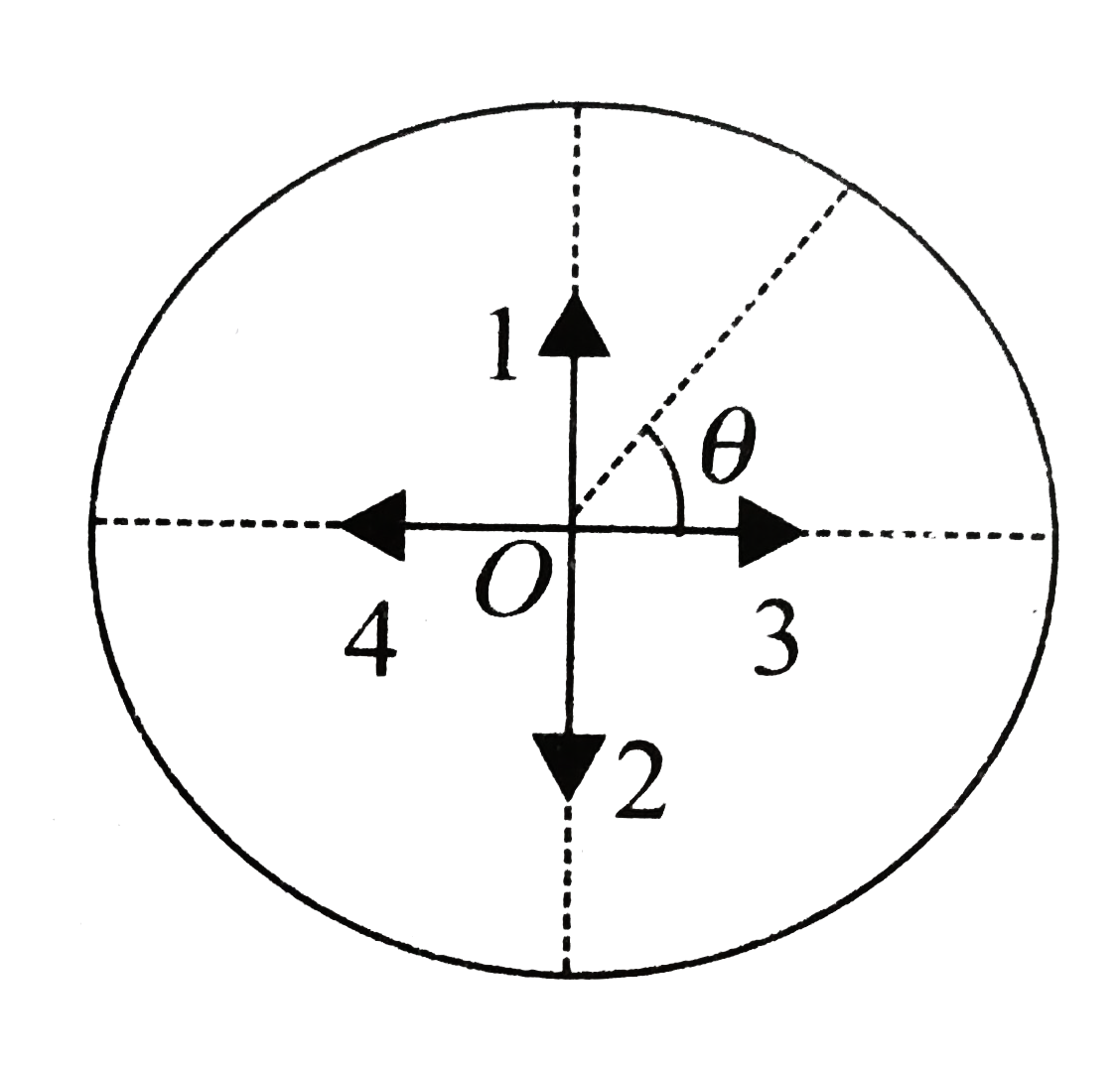
along 1 if $q_{0}$ is positive and 2 if $q_{0}$ is negative.

B

along 2 if $q_{0}$ is positive and 1 if $q_{0}$ is negative.

C

along 3 if $q_{0}$ is positive and 4 if $q_{0}$ is negative.

D

along 4 if $q_{0}$ is positive and 3 if $q_{0}$ is negative.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

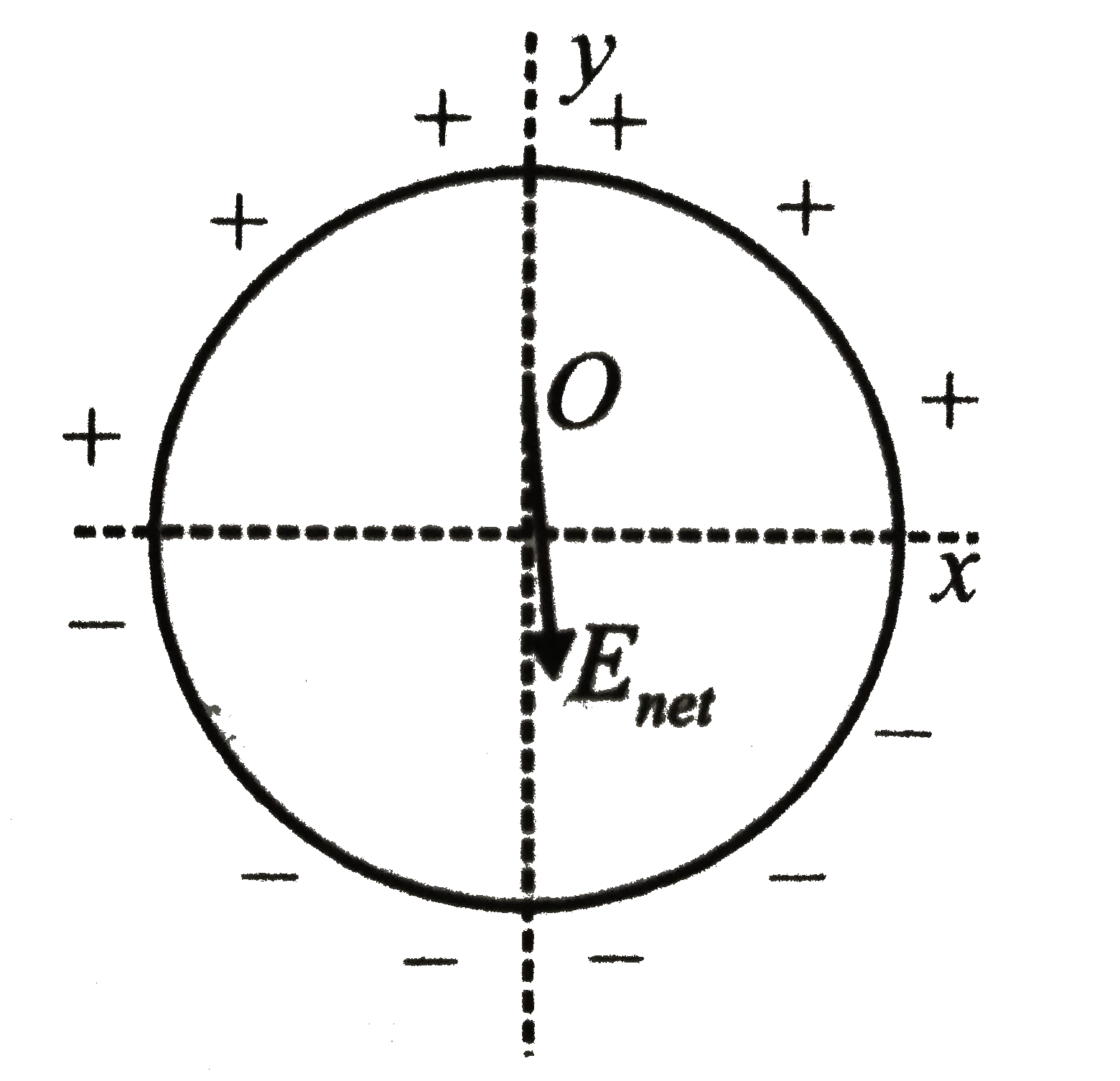
For $θ \leq θ < 2 π, λ$ is negative and symmmetrically distributed about $y -$ axix.
Hence direction of electric Beld $E_{ne}$ at $O$ due to charge distribution is in downward direction, If $q_{0}$ is

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The dimensional formula of linear charge density $λ$ is
A $[M^{- 1} L^{- 1} T^{+ 1} A]$
B $[M^{0} L^{- 1} T^{+ 1} A]$
C $[M^{- 1} L^{- 1} T^{+ 1} A^{- 1}]$
D $[M^{0} L^{- 1} T^{+ 1} A^{- 1}]$
Question 2 - Select One
A thin non-conducting ring of radius $R$ has a linear charge density $λ = λ_{0} cos θ$ , where $θ$ is measured as shown. The total electric dipole moment of the charge distribution is

A $R^{2} λ_{0}$
B $2 π R^{2} λ_{0}$
C $\frac{π R^{2} λ_{0}}{2}$
D $π R^{2} λ_{0}$
Question 3 - Select One
A half ring of radius R has a charge of $λ$ per unit length. The electric force on 1C charged placed at the center is
Azero
B $\frac{k λ}{R}$
C $\frac{2 k λ}{R}$
D $(k π λ) R$

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 3-True and False

Home
Ask Doubt
Profile