Charge on the ring is given as λ=λ0cosθ C/m .Find dipole moment of the ring
Step by step video & image solution for Charge on the ring is given as lambda=lambda_(0)cos theta C/m .Find dipole moment of the ring by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A circular wire of radius r has a uniform linear charge density λ=λ0cos2θ, The total charge on the wire is απλ0r2 Find α.
View SolutionA circle of radius a has charge density given by λ=λ0cos2θ on its circumference, where λ0 is a positive constant and θ is the angular position of a point on the circle with respect to some reference line. The potential at the centre of the circle is
View Solution
Knowledge Check
- Question 1 - Select One
The linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is
 Aλ0RB3λ0RC2λ0R3D2λ0R
Aλ0RB3λ0RC2λ0R3D2λ0R - Question 2 - Select One
Charge over a nonconducting ring is distributed so that the linear charge density varies as λ=λ0sinθ. What is the direction of force on a charge q0 placed at the center?
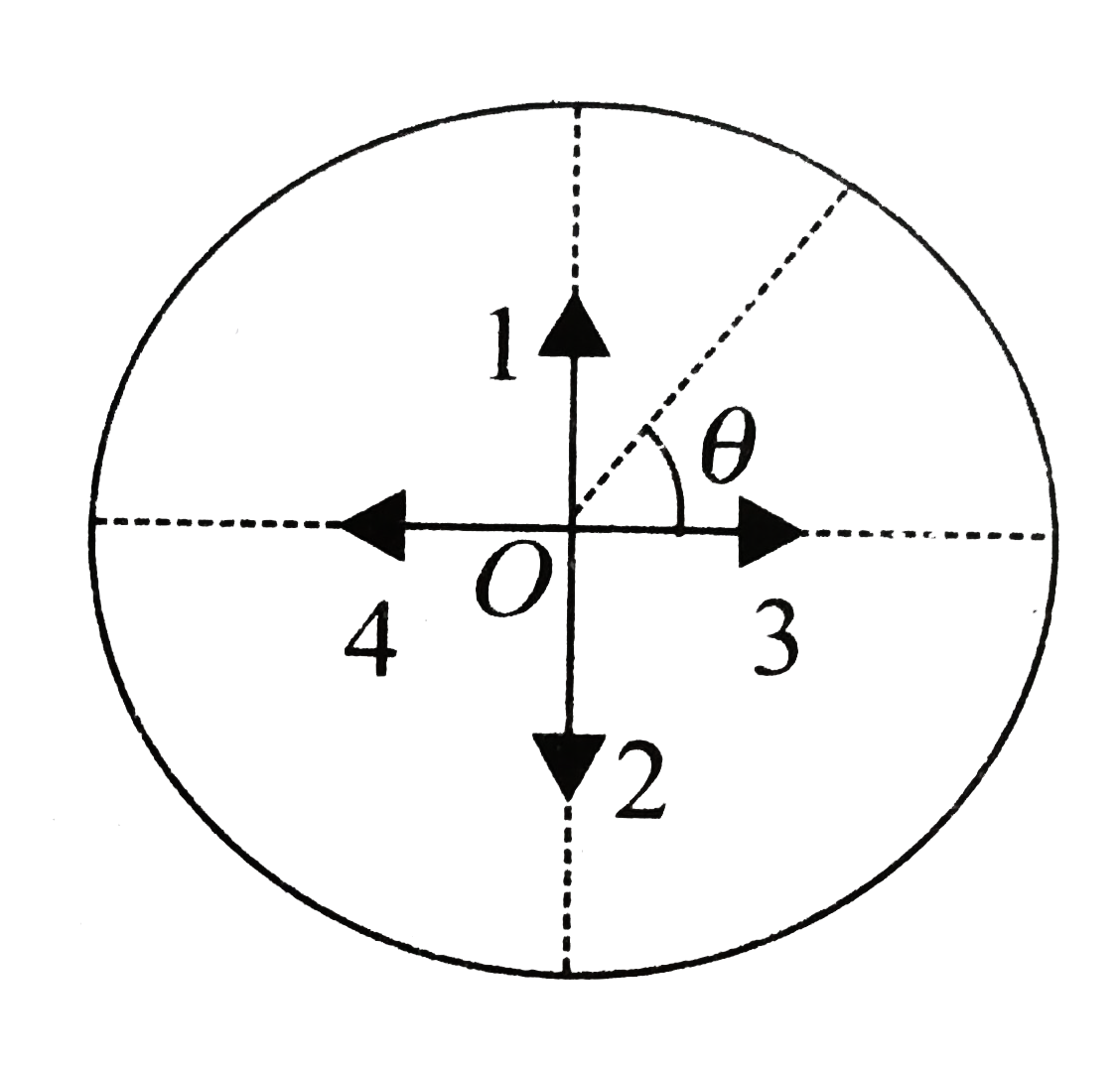 Aalong 1 if q0 is positive and 2 if q0 is negative.Balong 2 if q0 is positive and 1 if q0 is negative.Calong 3 if q0 is positive and 4 if q0 is negative.Dalong 4 if q0 is positive and 3 if q0 is negative.
Aalong 1 if q0 is positive and 2 if q0 is negative.Balong 2 if q0 is positive and 1 if q0 is negative.Calong 3 if q0 is positive and 4 if q0 is negative.Dalong 4 if q0 is positive and 3 if q0 is negative. - Question 3 - Select One
A charge q is spread uniformly over an isolated ring of radius 'R'. The ring is rotated about its natural axis and has magnetic dipole moment of the ring as M. Angular velocity of rotation is
AM2qR2BM(qR)2C2MqR2DqM2R
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
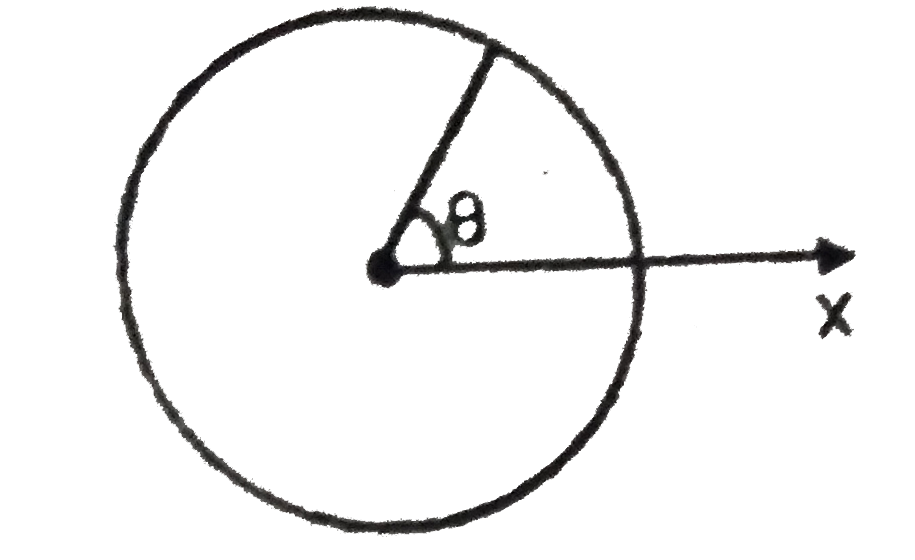 View Solution
View Solutionthe following diagram represents a semi circular wire of linear charge density λ=λ0sinθ where λ0is a positive constant.The electric potential at o is (take k=14πε0
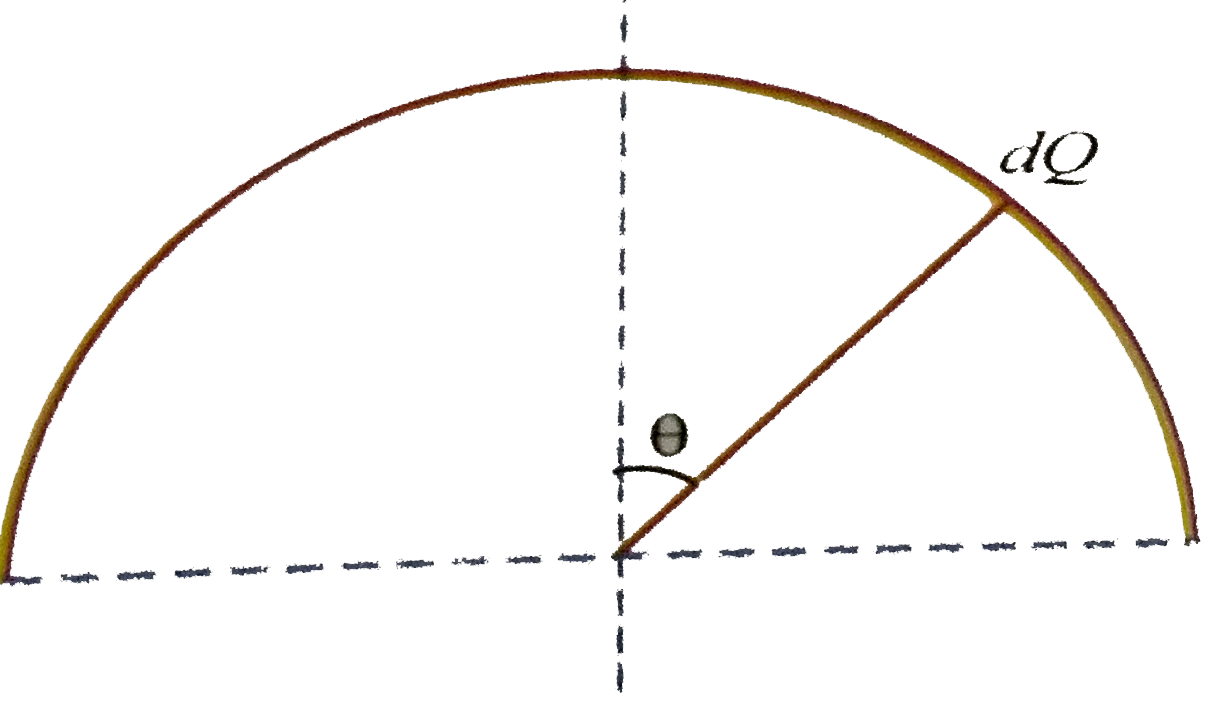 View Solution
View SolutionA thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
 View Solution
View SolutionA semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
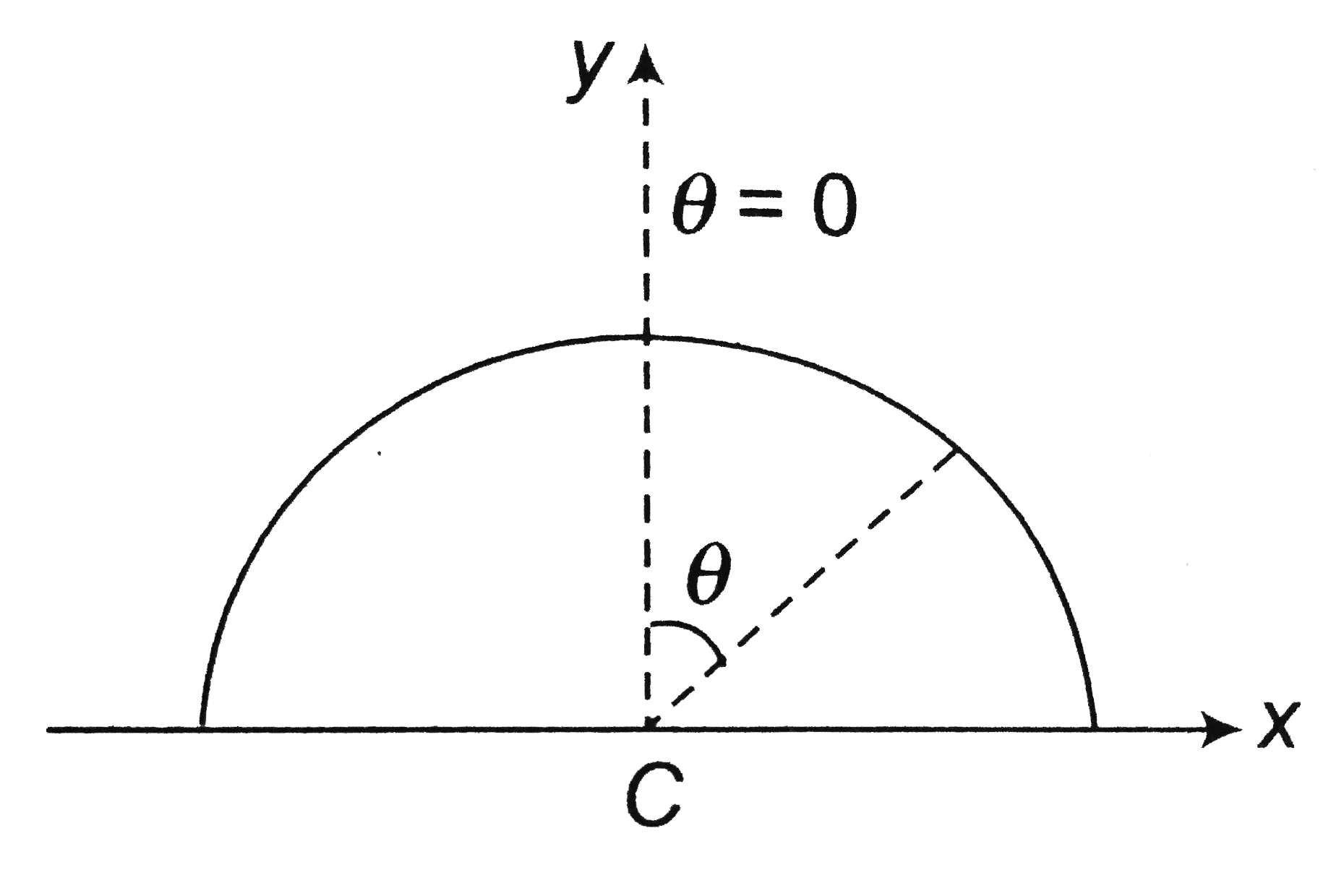 View Solution
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View Solution
