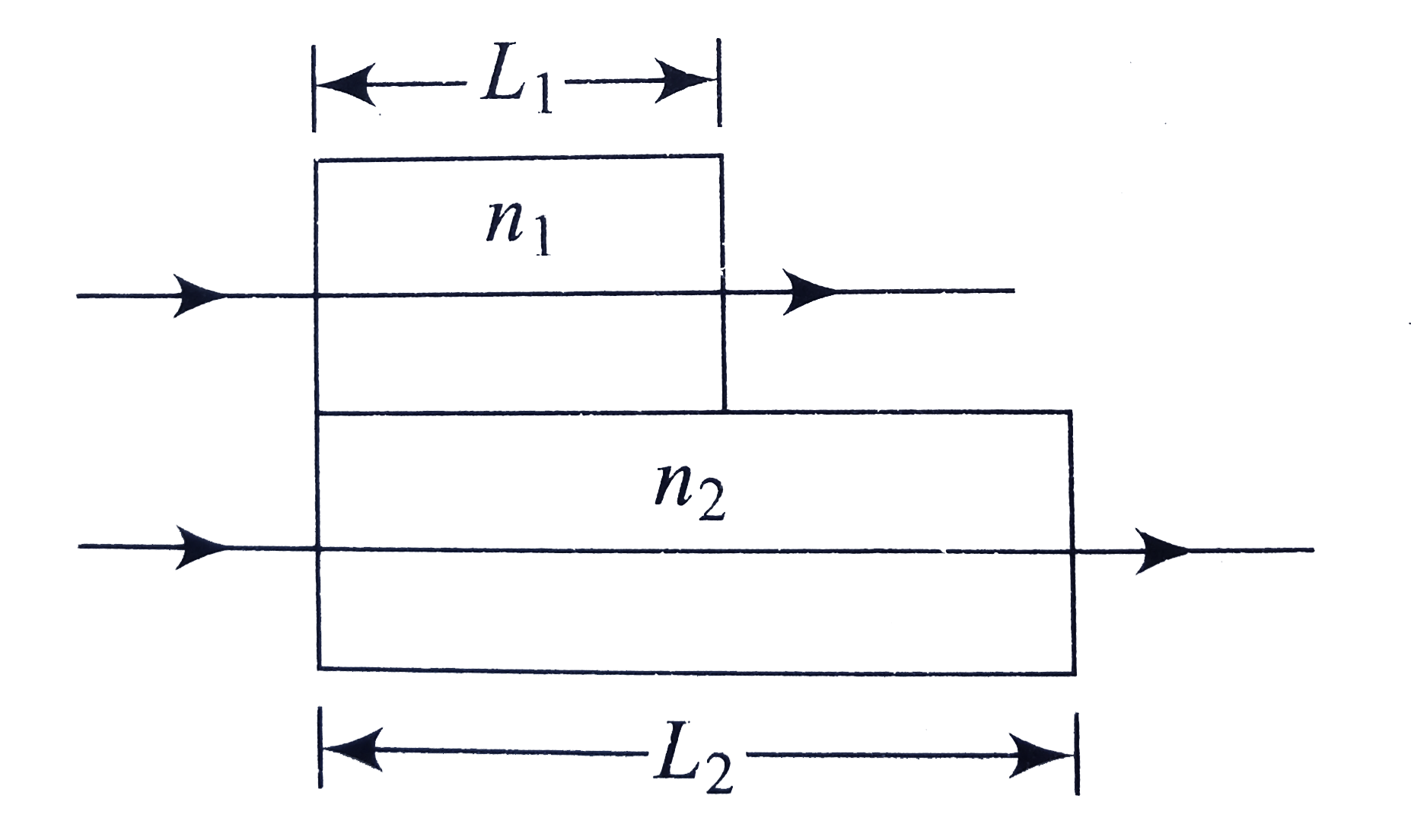
Two waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
0.8μm
1.2μm
1.7μm
2.9μm
The correct Answer is:b
Δx=path difference between two light waves
=[n1L1+L2−L1]−[n2L2]
Δϕ= phase difference between two waves
For longest wavelengths, Δϕ is the smallest.
For constructive interference, Δϕ=2π
Imax=n1L1−n2L2+(L2−L1)
(1.7)(3.5×10−6)−(1.25)(5.0×10−6)
+(5.0−3.5)×10−6
=(5.95−6.25+1.5)×10−6=1.2510−6m
=1.2μm
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
In Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero
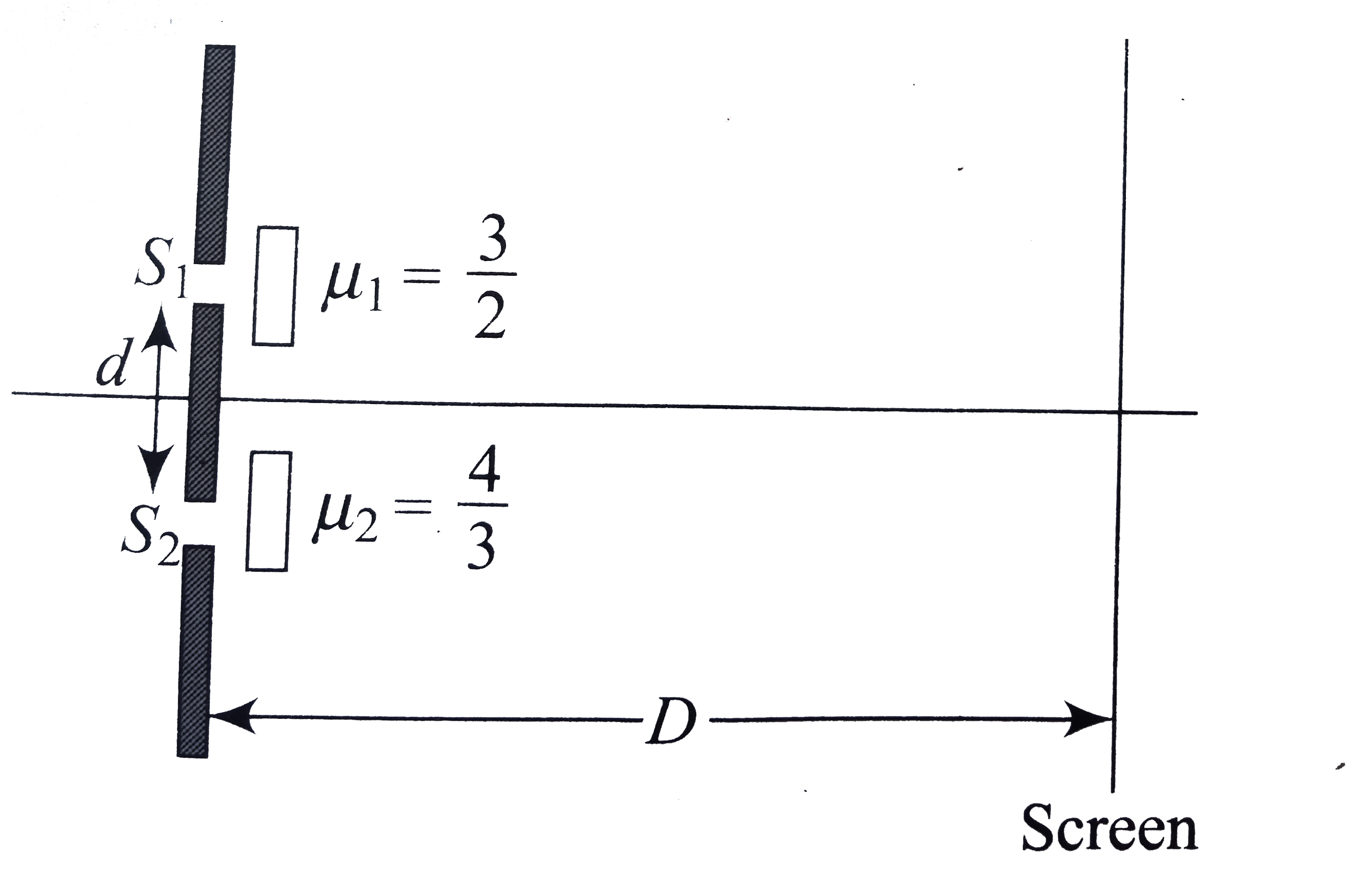
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionA hollow double concave lens is made of very thin transparent material. It can be filled with air or either of two liquids L_(1) or L_(2) having refractive indices n_(1) and n_(2) , respectively (n_(2) gt n_(1) gt 1) . The lens will diverge parallel beam of light if it is filles with
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionAs shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is N_(2) for Ray 2 and N_(1) for Ray 1. In the following table, values of N_(1) and N_(2) are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations 1 2 3 4 N_(1) 2.75 1.80 3.00 3.25 N_(2) 2.75 2.80 3.25 4.00
View SolutionTwo separated sources emit sinusoidal travelling waves but have the same wavelength lambda and are in phase at their respective sources . One travels a distance l_(1) to get to the observeration point while the other travels a distance l_(2) . The amplitude is minimum at the observation point , l_(1) - l_(2) is an
View SolutionLight of wavelength 5000Å is travelling in air. A thin glass plate (mu=1.5) of thickness 1mm is placed in the path of light. The change in phase of light is
View SolutionTwo light rays having the same wavelength lambda in vacuum are in phase initially. Then the first ray travels a path L_(1) through a medium of refractive index n_(1) while the second ray travels a path of length L_(2) through a medium of refractive index n_(2) . The two waves are then combined to observe interference. The phase difference between the two waves is :
View Solution
Two waves of light in air, of wavelength λ=600.0nm, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with L_(1)= 4.00 mu m, L_(2)= 3.50 mu m, n_(1) = 1.42, and n2=1.60. (a) What multiple of λ gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionAssume that two waves of light in air, of wavelength 585 nm, are initially in phase. One travels through a glass layer of index of refraction n1=160 and thickness L. The other travels through an equally thick plastic layer of index of refraction n2=1.50. (a) What is the smallest value L should have if the waves are to end up with a phase difference of 5.65 rad? (b) If the waves arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, intermediate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionTwo light waves having the same wavelength lambda in vocume are in phase initially. Then the first ray travels a path of length L_(1) through a medium of refractive index mu_(1) . The second ray travels a path of length L_(2) through a medium of refractive index mu_(2) . The two waves are then combined to observe interference effects. The phase difference between the two when they interfere, is
View SolutionNo. of waves of a certain colour light are 2000 in 1 mm distance in air, then what will be wavelength of light in medium of refractive Index 1.25 ?
View Solution
