Two identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
51 and 50
101 and 100
49 and 50
50 and 49
The correct Answer is:b
If the detector move by 0.5λ from origin, it observers 2nd maxima. So, after every 0.5λ, one maxima will be observed.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK34videos
THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK38videos
WAVES
Similar Questions
λ3−6λ2−15λ−8=0
View SolutionThe two coherent sources of monochromatic light of wavelength λ are located at a separation λ. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
View Solution
Knowledge Check
- Question 1 - Select One
Two coherent sources A & B emitting light of wavelength lambda are placed at position (-D,0) and (−D,3λ) respectively Here D >>λ The number of minima on y-axis and maxima on x-axis respectively are
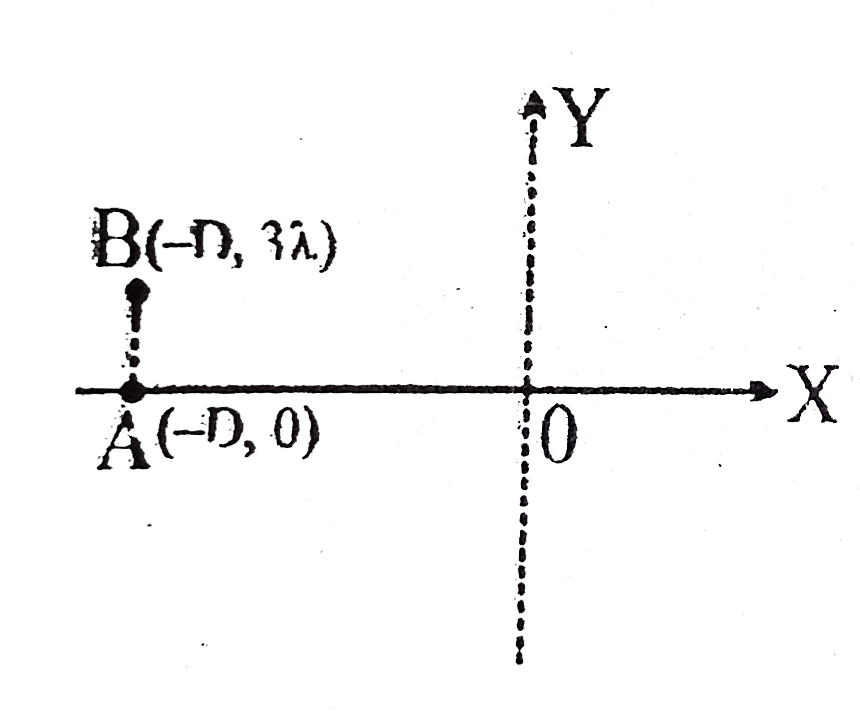 A6,5B5,6C4,3D3,4
A6,5B5,6C4,3D3,4 - Question 2 - Select One
Two coherent sources emit light of wavelength λ. Separation between them, d=4λ.
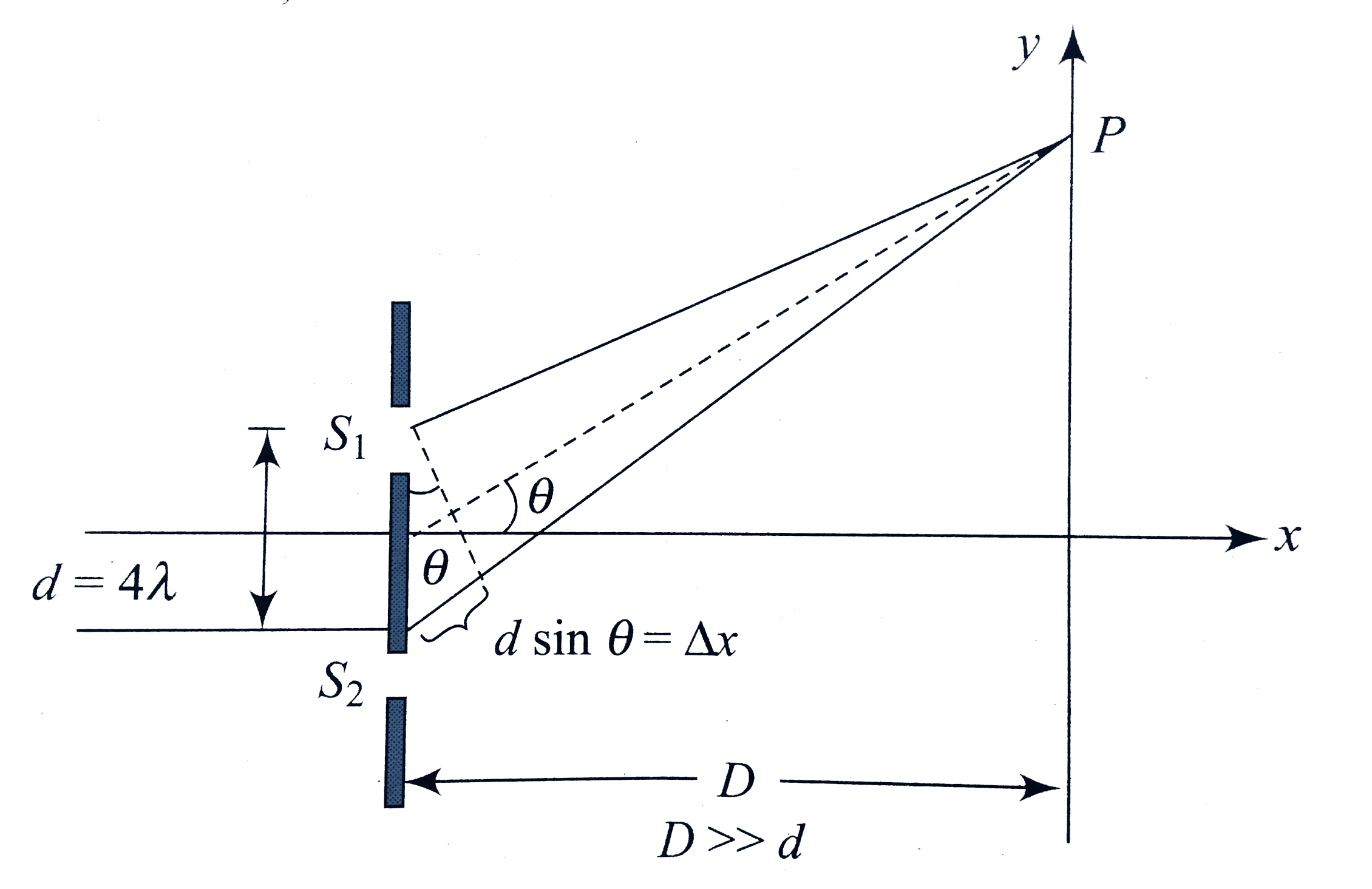
If a detector moves along the y-axis, what is the maximum number of minima observed?A6B9C5D4 - Question 3 - Select One
Two coherent light sources, each of wavelength λ, are separated by a distance 3λ, The maximum number of minima formed on line AB, which funs from −∞ to +∞, is
 A2B4C6D8
A2B4C6D8
An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionFor all λ∈R, The equation ax2+(b−λ)x+(a−b−λ)=0,a≠0 has real roots. Then
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
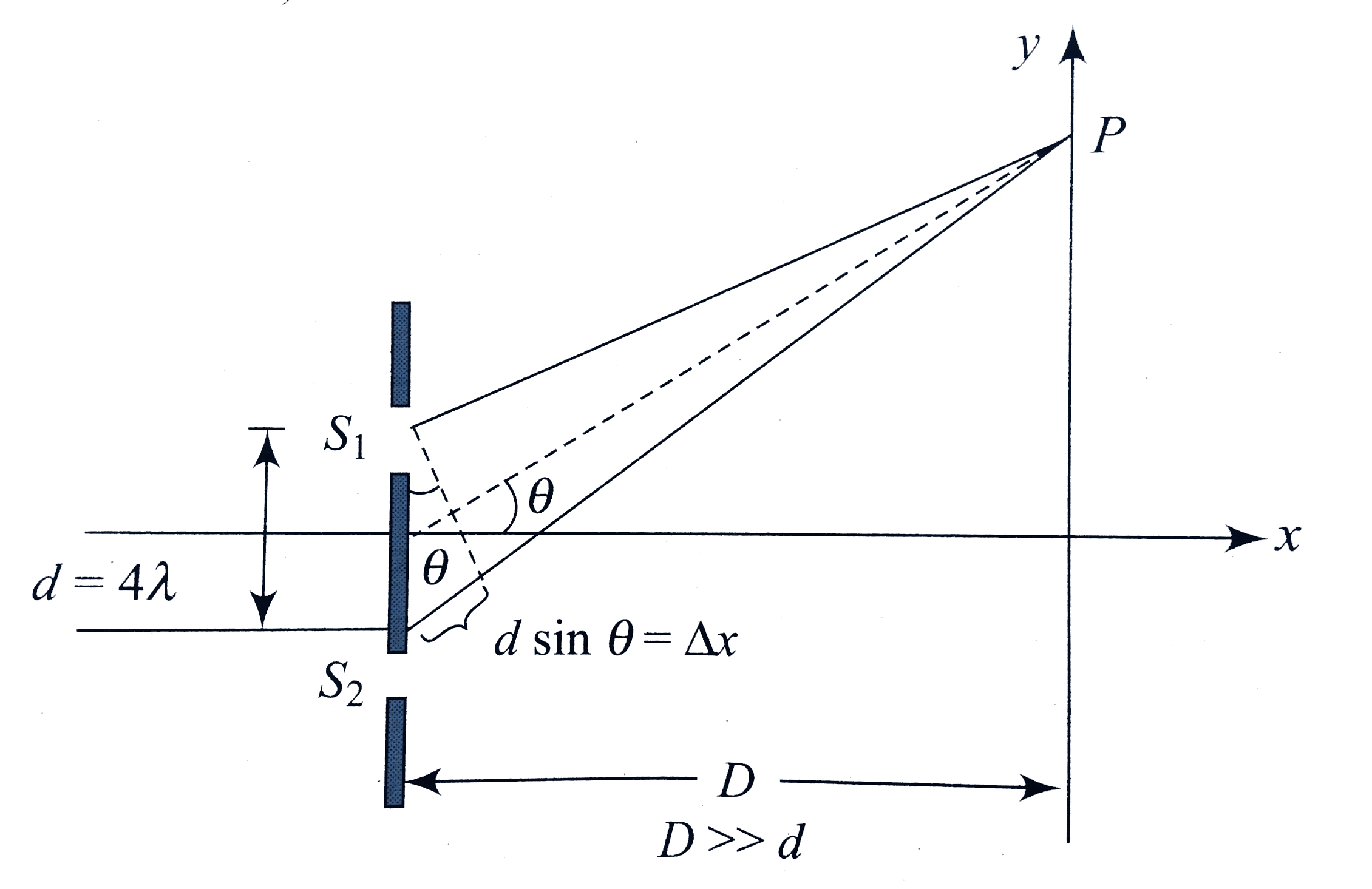
If a detector moves along the y-axis, what is the maximum number of minima observed?
If the detector moves along 'x-axis beginning from S2, the maximum number of minima observed isView SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
 View Solution
View SolutionIf λv,λx and λm represents the wavelength of visible light X-ray and microwave respectively then :
View Solution

