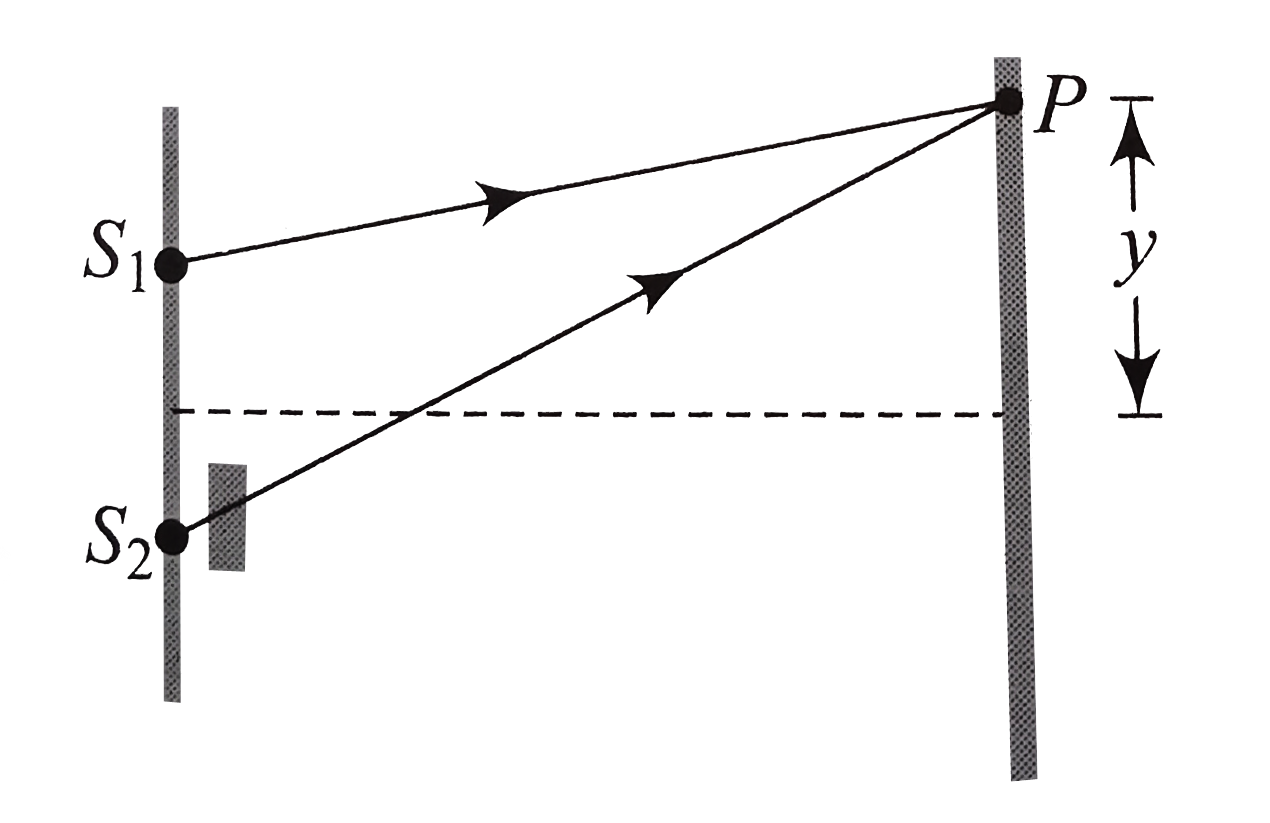
Young's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.

The phase difference at point P without inserting the slab is
3π/4
π/4
π/2
π/3
The correct Answer is:c
Without inserting the slab, path difference at P,
Δx=ydD=0.15×10−3×2×10−32=1.5×10−7m
Corresponding phase difference at P,
ϕ=(2πλ)(Δx)
=(2π6000×10−10)(1.5×10−7)=π2
ϕ2=π4
Therefore, intensity at P,
I=4I0cos2(ϕ/2)=2I0
Phase difference after placing to glass sheet,
ϕ'=ϕ+2πλ(μ−1)t
=π2+2π6000×10−10(1.5−1)(8000×10−19)
=11π6
Now, the intensity at P is,
I'=I0+ηI0+2√ηI20cos.11π6=2I0 (given)
solving this equation, we get η=0.21.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
View SolutionA light wave of frequency 5×1014Hz enters a medium of refractive index 1.5. In the velocity of the light wave is ….. And its wavelength is ……
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionYoung's double-slit experiment setup with ligth of wavelength lambda = 6000 Å , distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction eta of the incident light to pass through) and thickness 8000 Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change. Intensity at point P is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
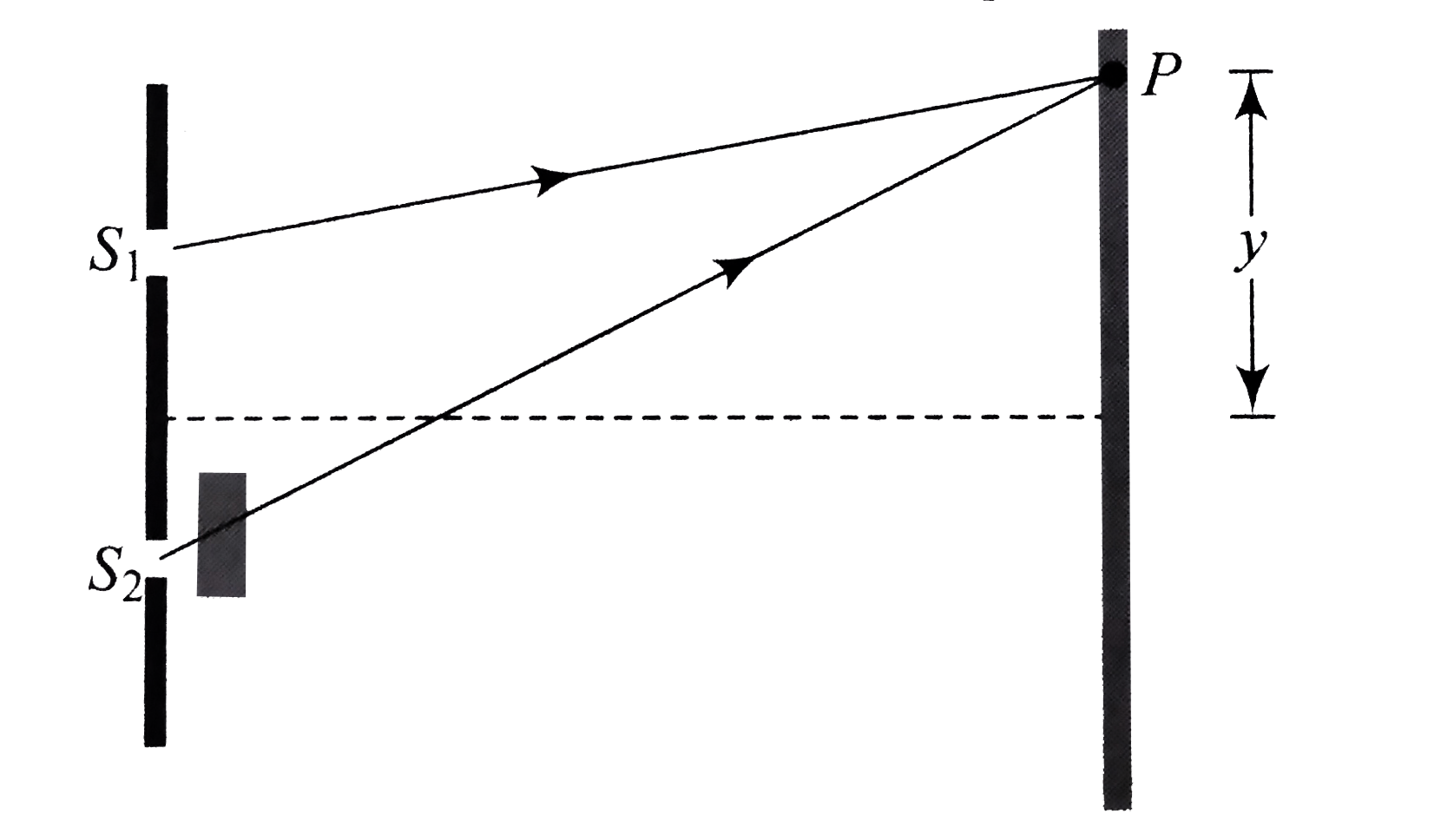
The value of η is
View SolutionIn Young's experiment , the distance of the screen from the two slits is 1.0 m . When a light of wavelength 6000 Å is allowed to fall on the slits , the width of the fringes obtained on the screen is 2.0 mm . Determine (a) the distance between the two slits and (b) the width of fringe if the wavelength of the incident light is 4800 Å.
View Solutionयंग के दो – स्लिट प्रयोग में पर्दे को स्लिटों से 1.0 मीटर की दूरी पर रखने पर व्यतिकरण फ्रिन्जो की चौडाई 0.02 सेमी पायी गई है। प्रकाश की तरंगदैर्ध्य 6000Å है। स्लिटों के बीच दूरी ज्ञात कीजिए।
View SolutionThe distance between the two slits in Young's double slit experiment is 0.02 cm. Interference fringes for light of wavelength 6000 Å are formed on the screen at a distance of 80 cm from the slits. Determine the distance of the fifth bright fringe.
View SolutionIn Young's double slit experiment the distance of the screen from the plane of the slits is 1.0 m. The wavelength of light used and width of the fringe are 6000 Å and 2 mm respectively. Distance between the slits is
View SolutionIn Young's double slit experiment the distance of the screen from the plane of the slits is 1.0 m. The wavelength of light used and width of the fringe are 6000 Å and 2 mm respectively.
If the wavelength of the light used is 4800 Å, the width of the fringe will be
View Solutionयंग के द्विस्लिट प्रयोग में स्लिटों के बीच की दुरी 2 मिमी, स्लिटों से पर्दे की दुरी 10 सेमी तथा प्रयुक्त प्रकाश की तरंगदैर्ध्य 6000Å है | एक स्लिट के सामने मोटाई 0⋅5 मिमी की काँच की प्लेट रखने पर व्यतिकरण चित्र 5 मिमी सरक जाता है | प्लेट का अपवर्तनांक ज्ञात कीजिए |
View SolutionIn a Young's double-slit experiment, the slit separation is 0.2 mm and the distance between the screen and double-slit is 1.0 m. wavelength of light used is 5000 Å. The distance between two consecutive dark fringes is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.

The phase difference at point P without inserting the slab is
View Solution
