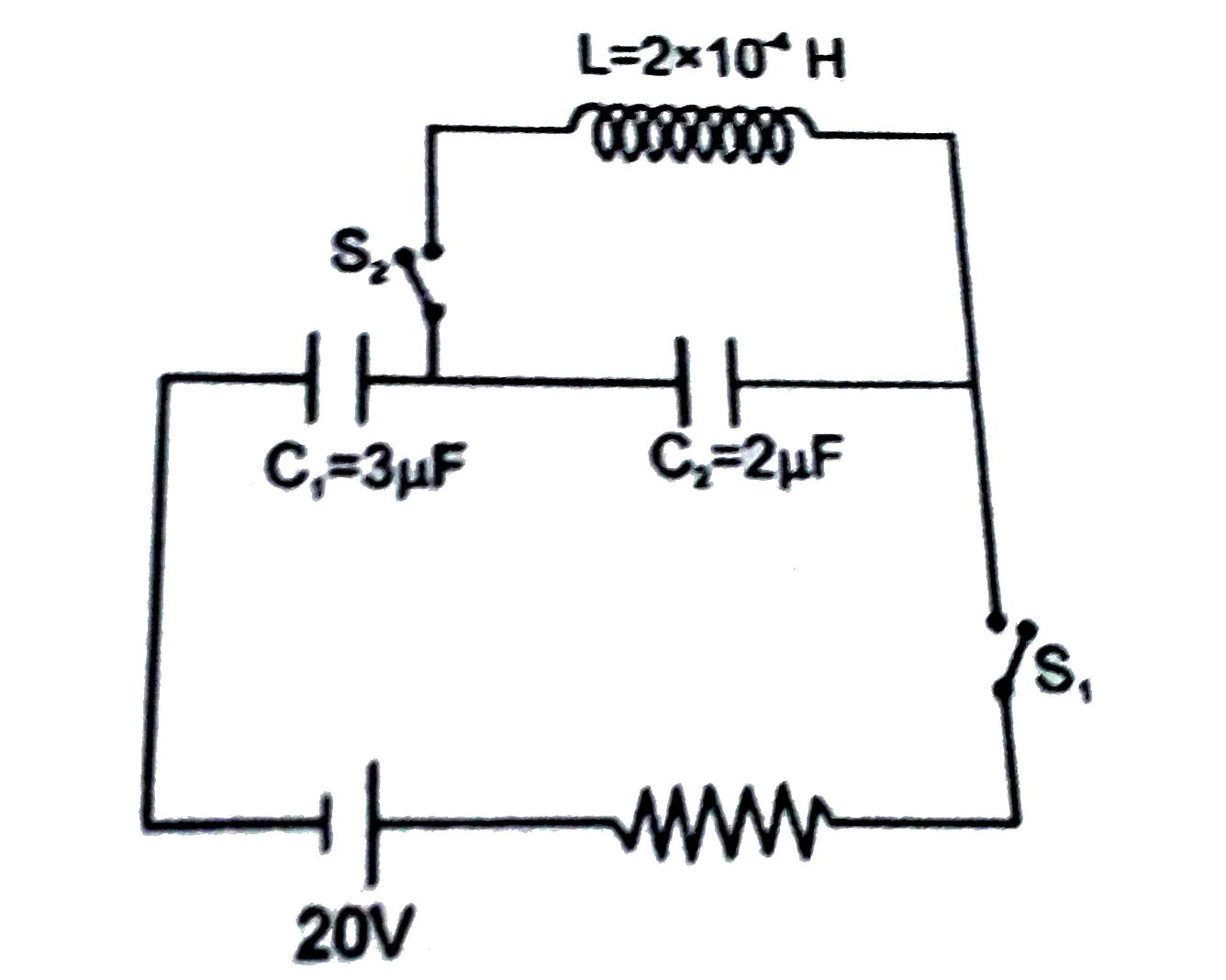
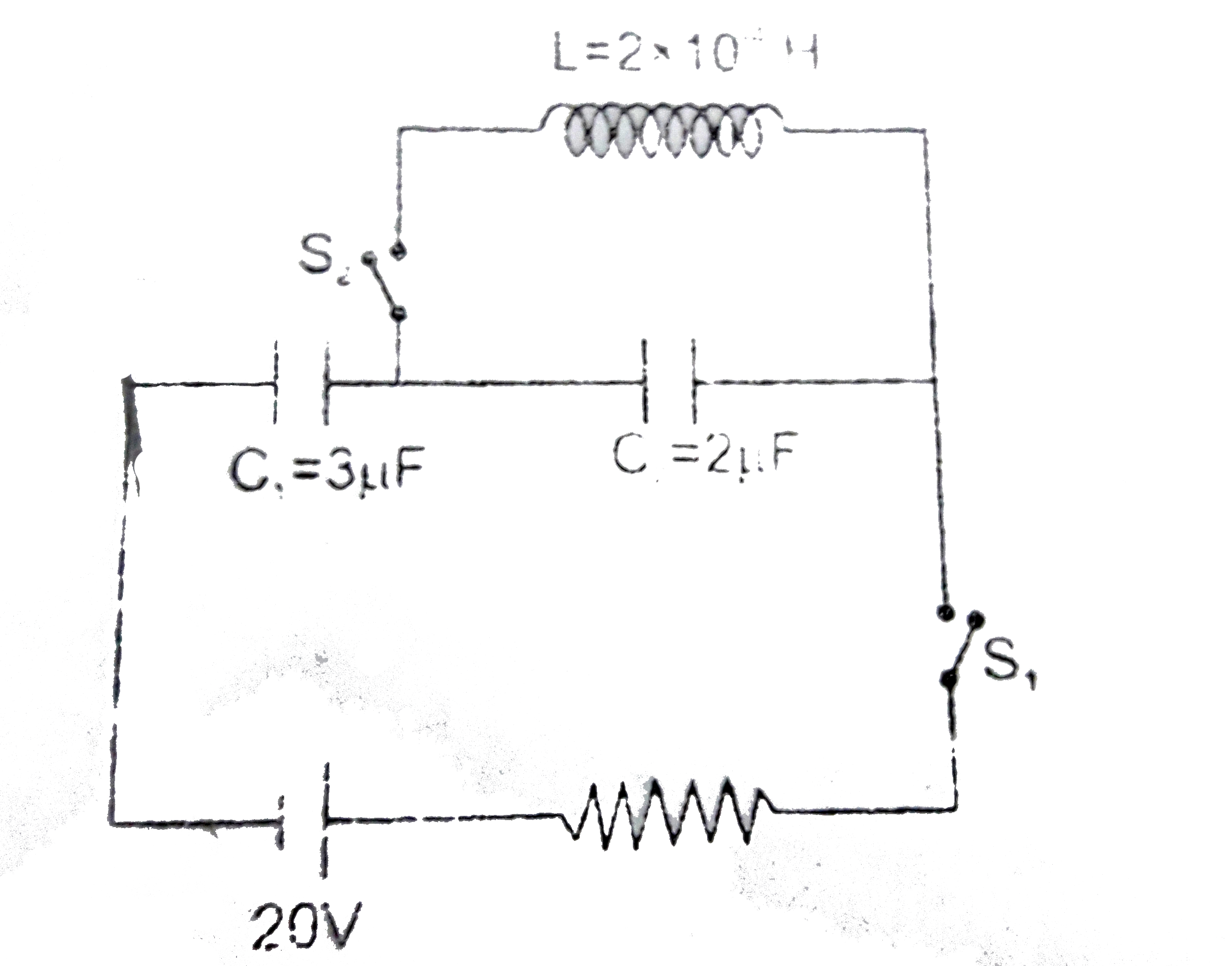
A circuit containing capacitors C1andC2 shown in Fig. is in the steady state with key K1 closed. At the instant t = 0, K1 is opened and K2 is closed. The angular frequency of oscillation of the circuit and charge across C1att=125(μ)s are respectively
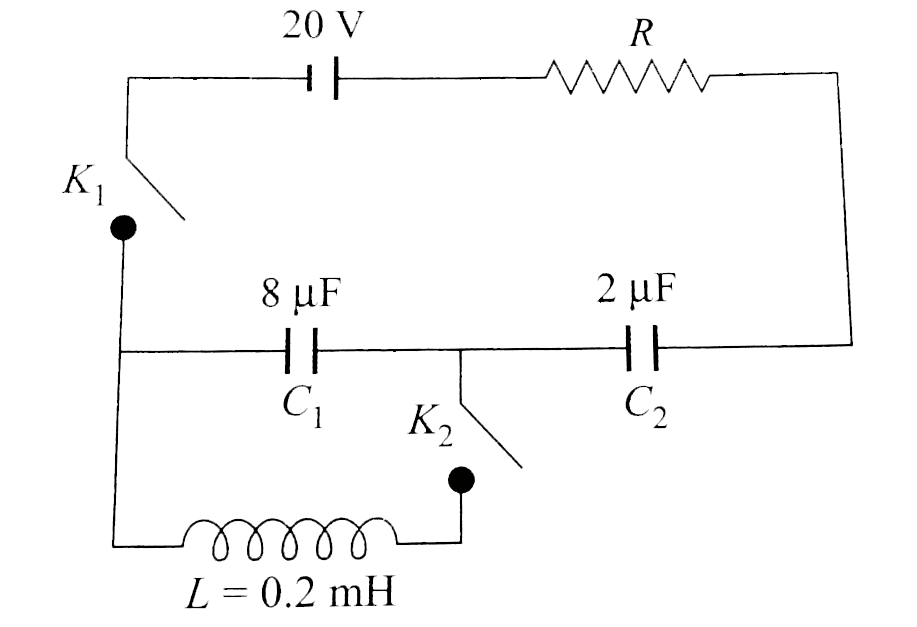
25×103rads−1,32(μ)C
5×104rads−1,16(μ)C
5×104rads−1,−16(μ)C
25×103rads−1,−32(μ)C
The correct Answer is:D
Angular frequency of oscillation
ω=1√LC=1√0.2×10−3×8×10−6
=2.5×104rad/s=25×103rad/s
QC1−LdIdt=0⇒QC1+Ld2Qdt2=0
The solution of this equation is Q=(Q0)sin(ωt+ϕ)
where at t=0,Q=Q0
Q0=CeqV=C1C2C1+C2V
=8×2×10−12×2010×10−6=32×10−6C
ϕ=π2
Q=(32μC)cos(2.5×104×125×10−6)≅−32(μ)C.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Multiple Correct
Explore 34 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Linked Comprehension
Explore 84 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- Moving charges and magnetismBook:CENGAGE PHYSICSChapter:Moving charges and magnetismExercise:Question Bank
Explore 20 Videos
Similar Questions
A circuit containing capacitors C1 and C2 shown in the figure is in the steady state with key K1 cloesed. At the instant t=0 , K1 is opened and K2 is closed.
(a) Find the angular frequency of oscillation of the LC circuit.
(b) Determine the first instant t , when enregy in the indctor becomes one third of that in the capacitor.
(c) Calculate the change on the plates of the capacitor at that instant.
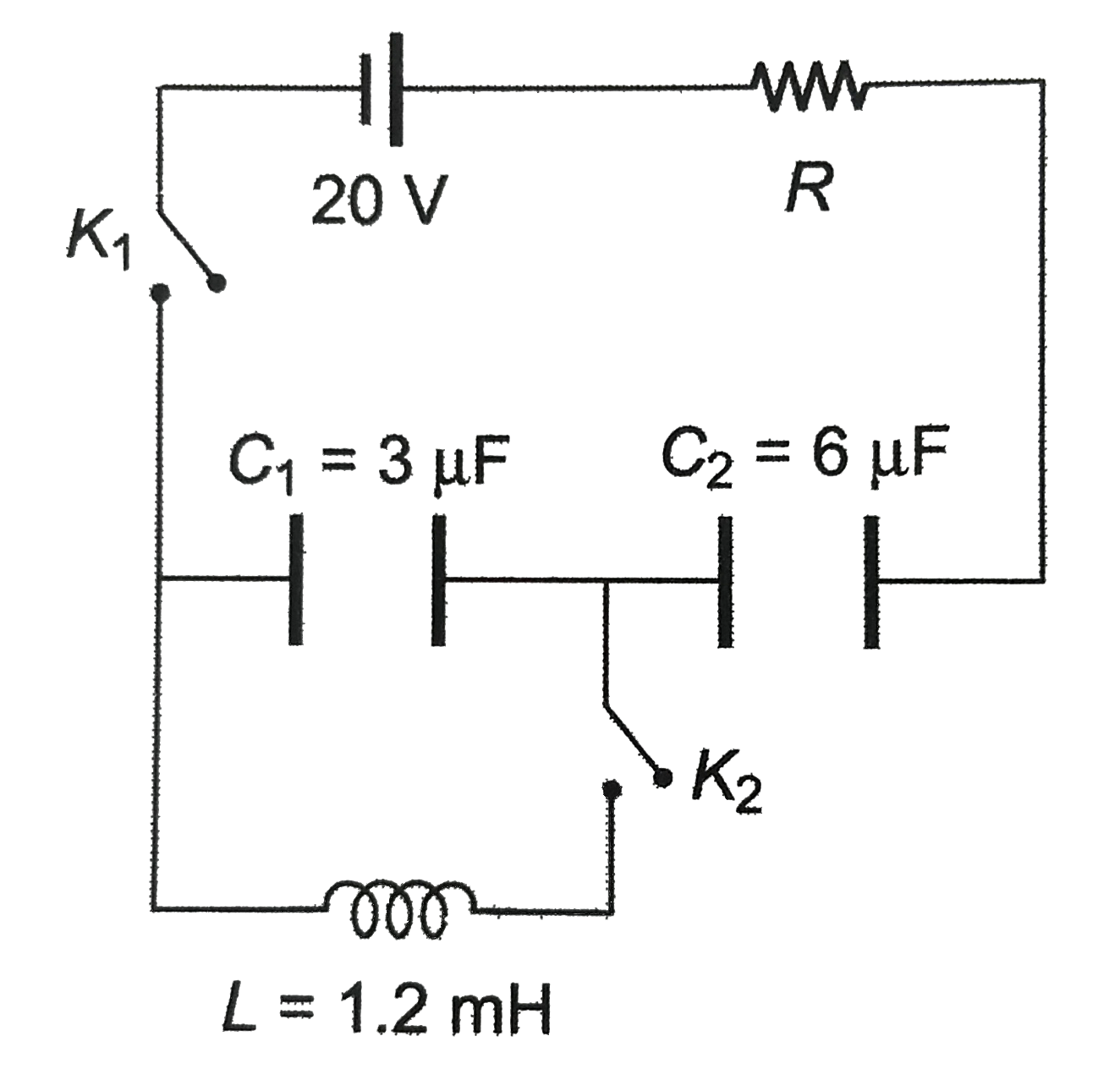
View SolutionA circuit containing capacitors C1 and C2, shown in the figure is in the steady state with key K1 and K2 opened. At the instant t=0, K1 is opened and K2 is closed.
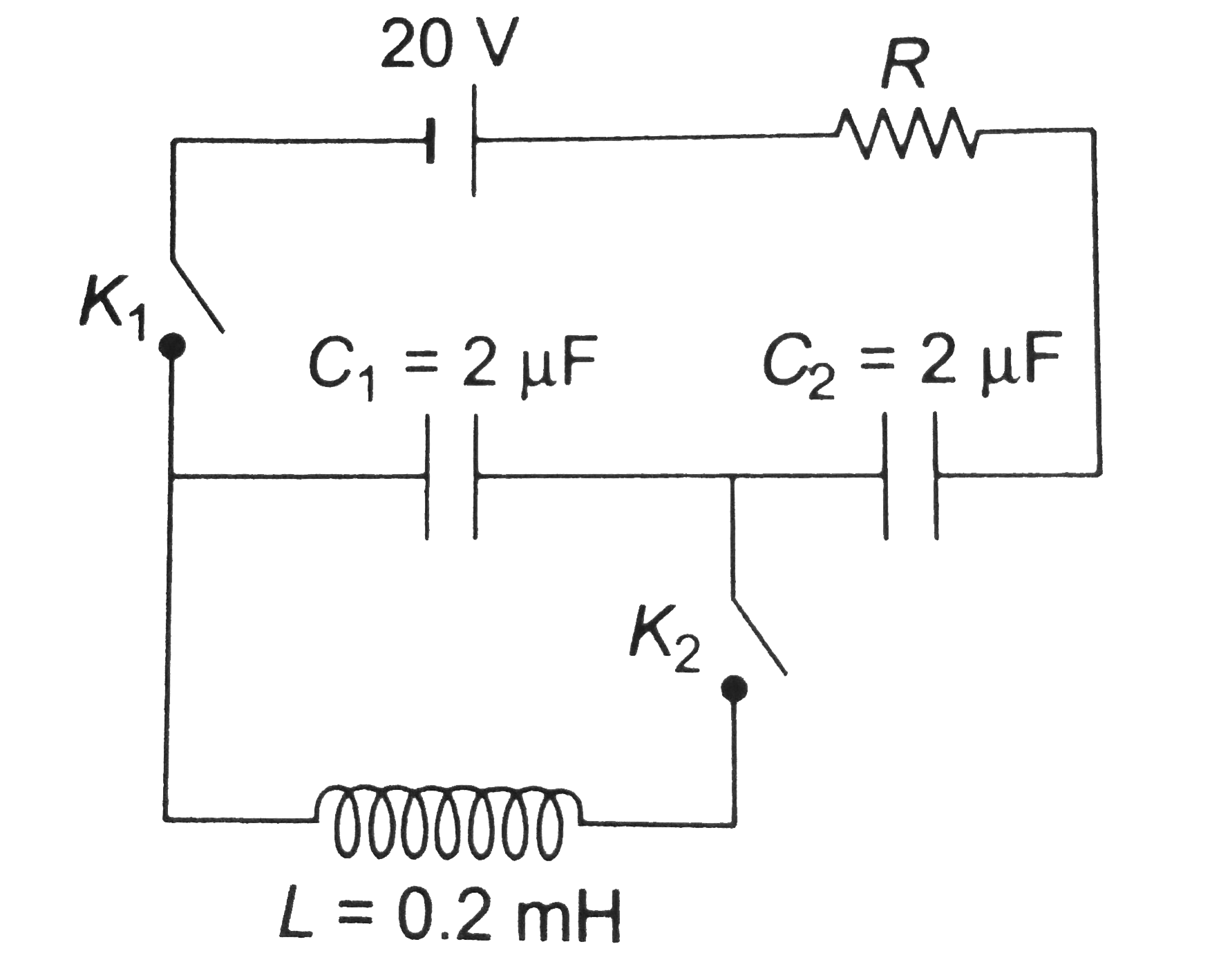
(a) Find the angular frequency of oscillations of L−C circuit.
(b) Determine the first instant t, when energy in the inductor becomes one third of that in the capacitor.
(c) Calculate the charge on the plates of the capacitor at that instant.
View Solution
Knowledge Check
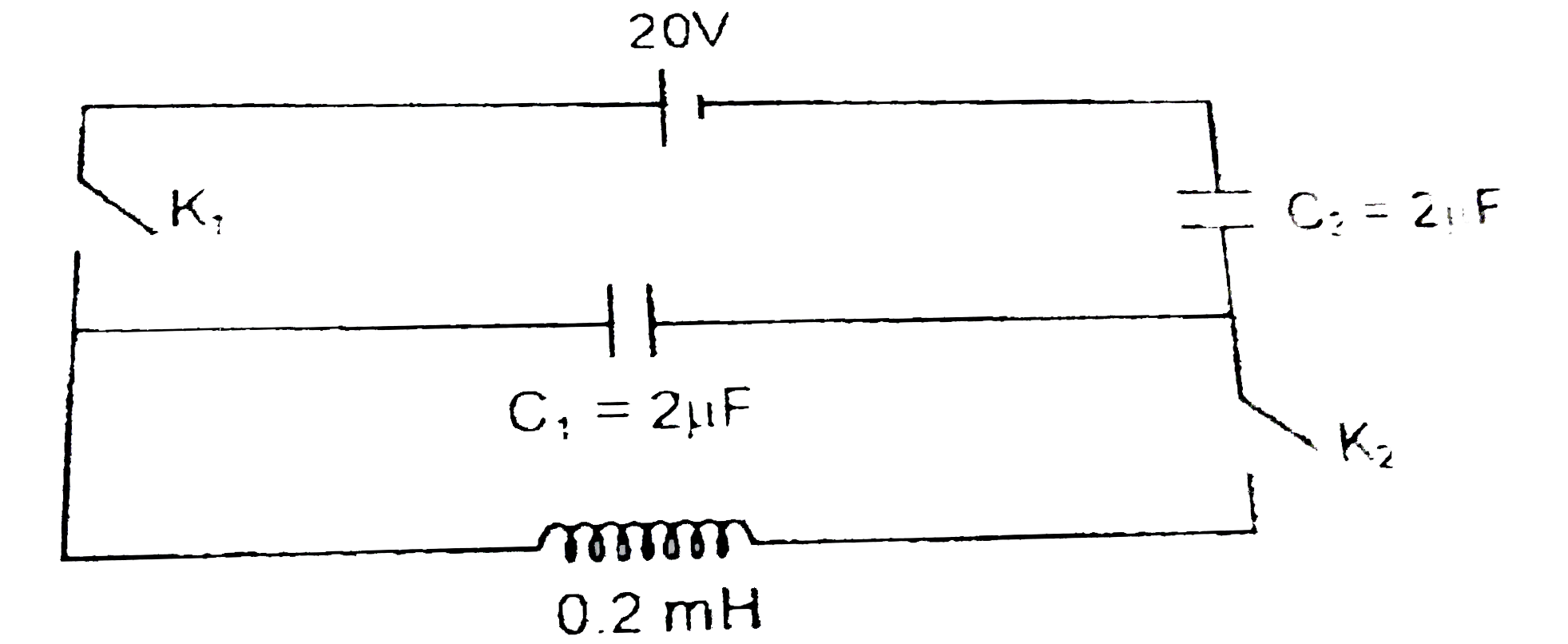
A circuit containing two capacitor C1 and C2 shown in figure is in steady state with switch K1 closed and K2 open. At the instant t=0,K1 is opened and K2 is closed. The correct statements are.AAngular frequency of oscillation of LC circuit is 5×104radsecBcharge on capacitor C1 at t=0 is 40μCCMaximum current in iductor is 1ADCharge on capacitor C1 is 10√3μC when energy in the inductor becomes one third of the energy in capacitor.In the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
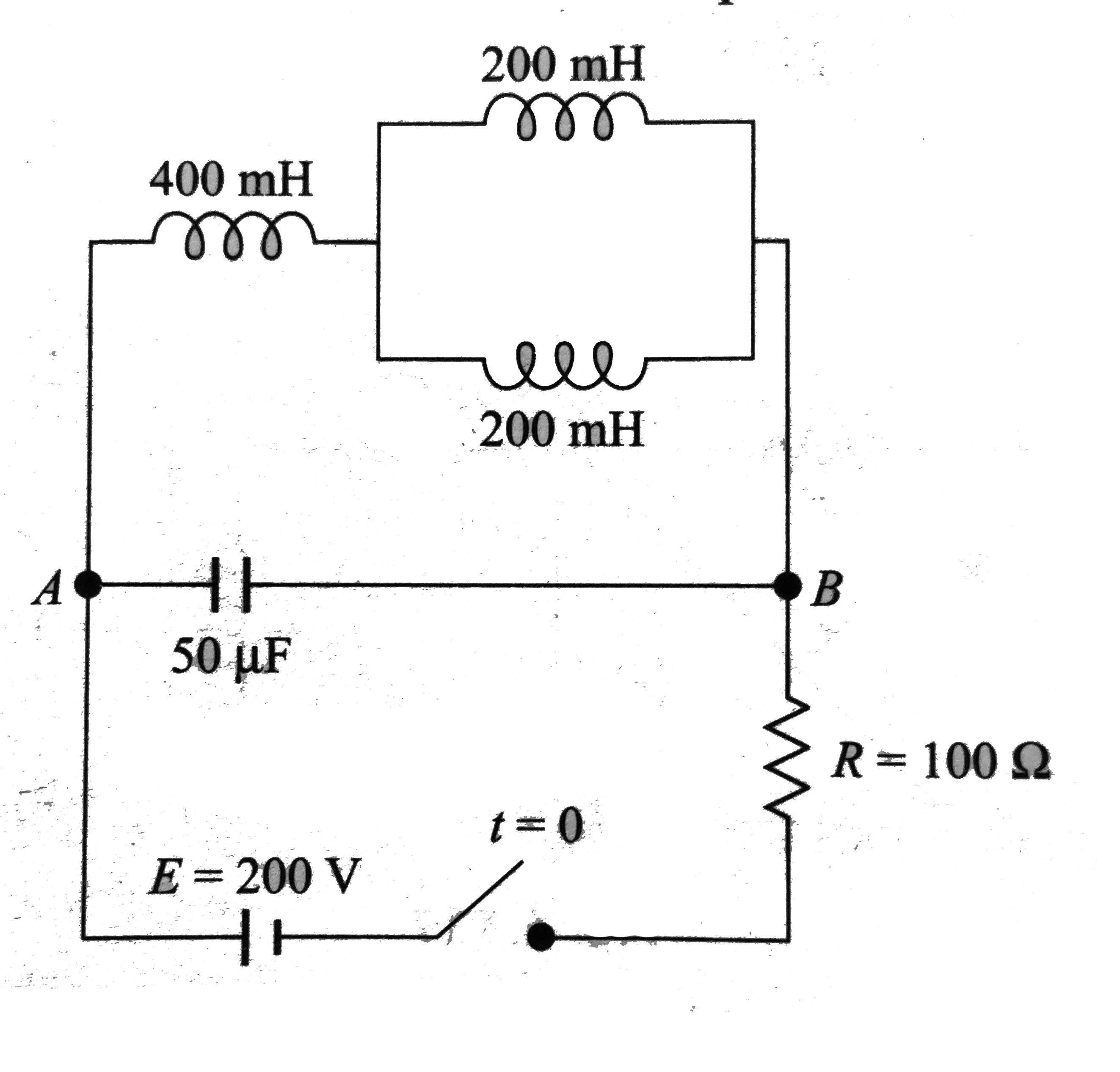
Find the angular frequency of oscillation of the charge on the capacitor.A100rads−1B200rads−1C300rads−1sD400rads−1For given circuit charge on capacitor C, and C2 in steady state will be equal to
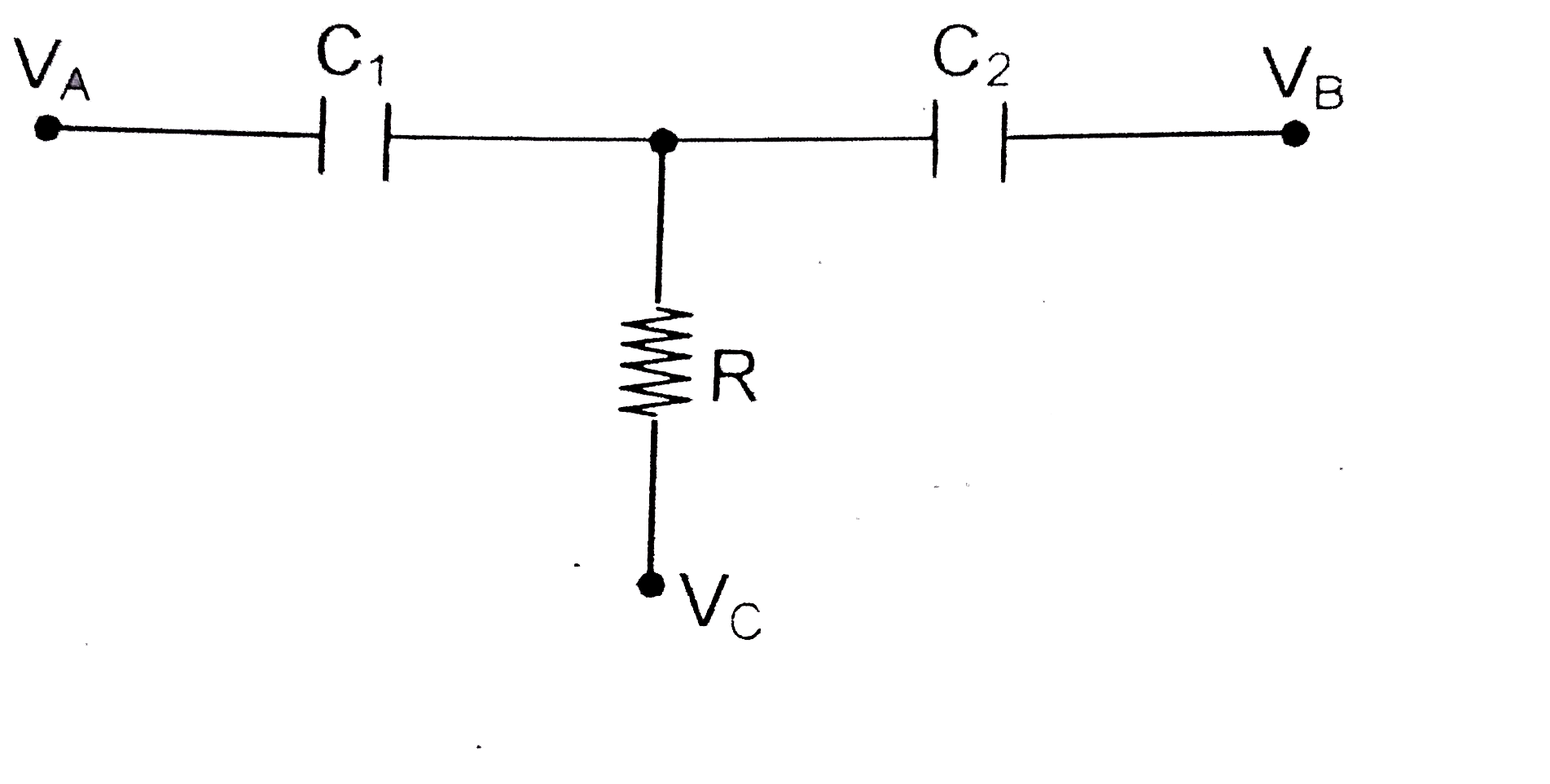 AC1(VA−Vc),(Vc−VB) respectivelyBC1(VA−VB),C2(VA−VB) respectivelyC(C1+C2)(VA−VB) on each capacitorD(C1C2C1+C2)(VA−VB) on each capacitor
AC1(VA−Vc),(Vc−VB) respectivelyBC1(VA−VB),C2(VA−VB) respectivelyC(C1+C2)(VA−VB) on each capacitorD(C1C2C1+C2)(VA−VB) on each capacitor
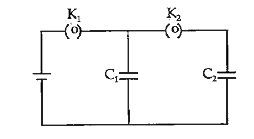
In the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.
Find the first instant t, when energy in inductor becomes one third of that in capacitor
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
View SolutionThe circuit shows in Fig. is in the steady state with switch S1 closed. At t=0,S1 is opened and switch S2 is closed.
a. Derive expression for the charge on capacitor C2 as a function of time.
b. Determine the first instant t, when the energy in the inductor becomes one-third of that in the capacitor.

View SolutionIn the circuit shows in Fig. switch k2 is open and switch k1 is closed at t=0. At time t=t0, switch k1 is opened and switch k2 is simultaneosuly closed. The variation of inductor current with time is
View Solution