In a magnetic field as shown, in Fig. two horizontal wires of same mass and length l1andl2 are free to slide on different vertical rails with velocities v1andv2 respectively. If the resistance of two circuits are same and a1anda2 are acceleration of two horizontal wires respectively, the condition for a1>a2 is

l1l2=v2v1
l1l2<(v2v1)1/2
l1l2>(v1v2)1/2
l1l2<v1v2
The correct Answer is:B
B2v1l21R−mg=ma1...(i)
B2v1l22R−mg=ma1−mg=ma2 ...(ii)
a1−a2=(B2mR)(v1l21−v2l22)
for a1>a2,v1l21>v2l22
l1l2>(v2v1)1/2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank20videos
Moving charges and magnetism
Similar Questions
Knowledge Check
- Question 1 - Select One
Two cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
At1t2Bt21t22Cmt1t2D√t1t2 - Question 2 - Select One
Two wires of same radius having lengths l1, and l2 and resistivities ρ1 and ρ2 are connected in series. The equivalent resistivity will be
Aρ1l2+ρ2l1ρ1+ρ2Bρ1l1+ρ2l2l1+l2Cρ1l1+ρ2l2l1−l2Dρ1l2+ρ2l1l1+l2 - Question 3 - Select One
Two wires of same radius having lengths l1andl2 and resistivities ρ1andρ2 are connected in series. The equivalent resistivity will be
Aρ1l2+ρ2l1ρ1+ρ2Bρ1l1+ρ2l2l1+l2Cρ1l1+ρ2l2l1−l2Dρ1l2+ρ2l1l1+l2
In an acute angled triangle ABC,AA1 and AA2 are the medians and altitudes respectively. Length A1A2 is equal to
View SolutionFind the mutual inductance of two concentric coils of radii a1 and a2(a1<<a2) if the planes of the coils are same.
 View Solution
View SolutionA uniform magnetic field passes through two areas, A1 and A2. The angles between the magnetic field and the normals of areas A1 and A2 are 30.0° and 60.0°, respectively. If the magnetic flux through the two areas is the same, what is the ratio A1/A2?
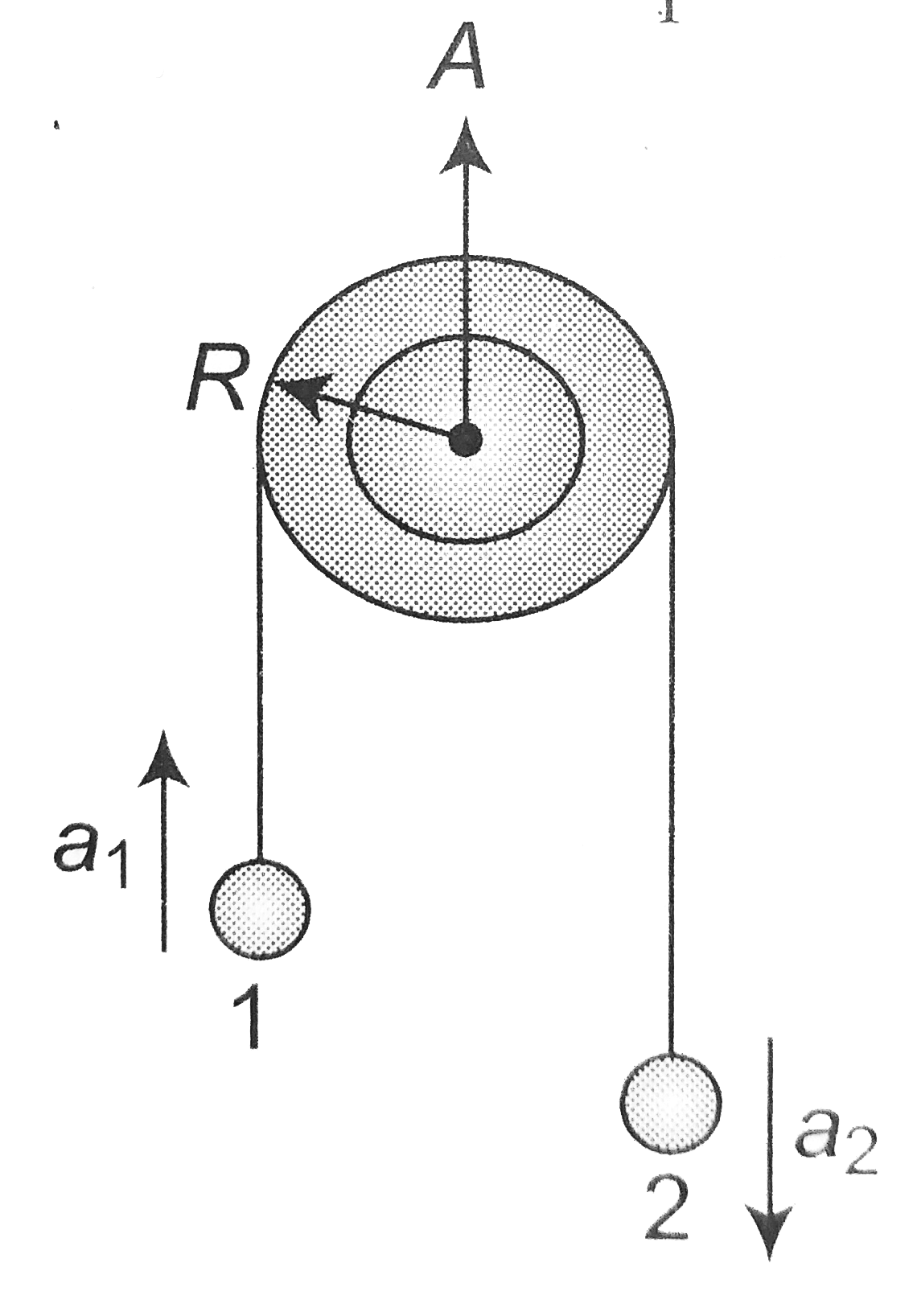
View SolutionTwo masses are connected by a string which passes over a pulley acceleration upward at a rate A shown. If a1 and a2 be the accelerations of bodies 1 and 2 respectively then,
 View Solution
View SolutionTwo wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
View Solution