A uniform rod of thermal conductivity of 65J/m−s−∘C is surrounded by an insulator on its sides. One of its ends is put in a furnace, while the other end is kept exposed. If the temperature gradient of the rod is −75∘C/m, find the emissive power of the exposed end.
If ΔQΔt is the rate of heat conduction through the rod from the end at the furnace to the exposed one, then
ΔQΔt=KA(−ΔTl)
Where A is the cross-sectional area and ΔTl the temperature ture gradient.
(ΔQΔt)1A=K(−ΔTl)
But (ΔQΔt)1A is the emissive power (E) of the free end.
E=K(−ΔTl)=65J/m−s−∘C×75∘C/m=4875W/m2\
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Single Correct148videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.318videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
The temperature gradient in a rod 0.5 m long is 40∘C per metre. The temperature of the hotter end is 30∘C. What is the temperature of its colder end?
View SolutionA cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
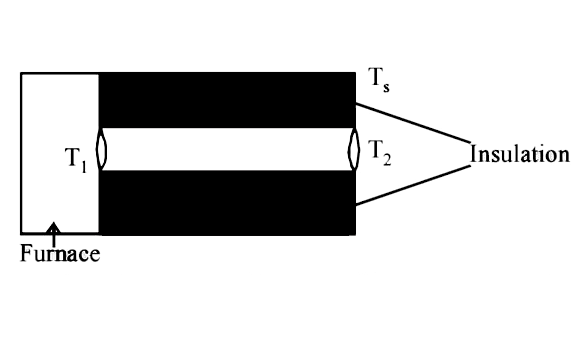 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The temperature gradient in a rod of 0.5 m long is 80∘C/m. If the temperature of hotter end of the rod is 30∘C, then the temperature of the colder end is
A40∘CB−10∘CC10∘CD0∘C - Question 2 - Select One
The temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
A40∘CB−10∘CC10∘CD0∘C - Question 3 - Select One or More
Two ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
AI∝ABI∝dTdlCI∝A∘DI∝1(dTdl)
A brass rod of length 1m is fixed to a vertical wall at one end, with the other end keeping free to expand. When the temperature of the rod is increased by 120∘C, the length increases by 3cm. What is the strain?
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
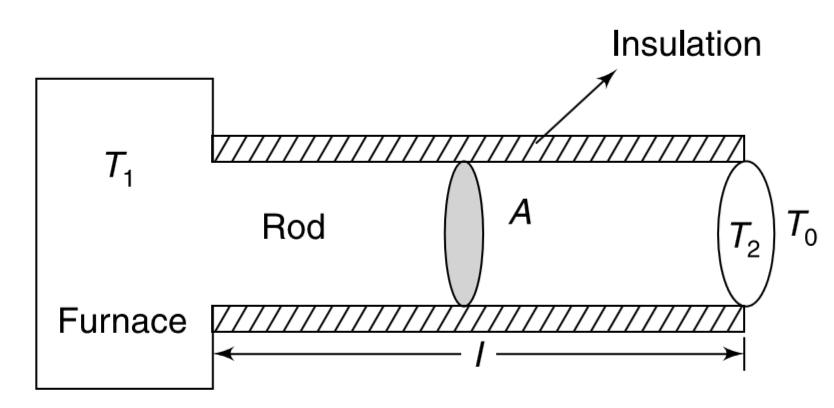 View Solution
View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .View Solution
.View SolutionA rod AB is 1m long. The temperature of its one end A is maintained at 100∘C and other end B at 10∘C, the temperature at a distance of 60 cm from point B is
View SolutionA uniform rod of mass M has an impulse applied at right angles to one end. If the other end begins to move with speed V, the magnitude of the impulse is
View Solution
