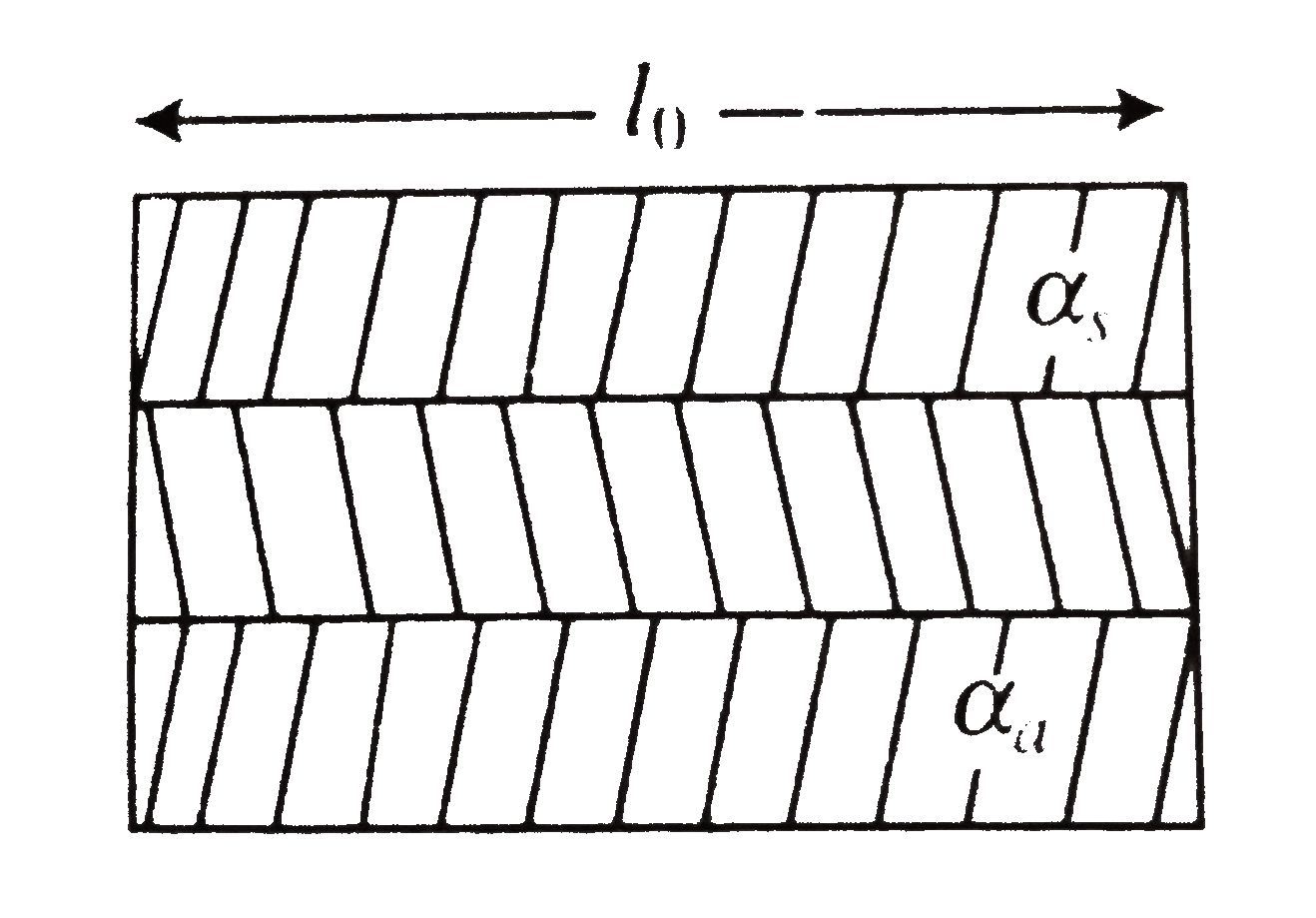
Two steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C
 . Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
At θ1
At θ2
If rods are free to expand,
lS=l0(1+αSθ)
lα=l0(1+αaθ)
Y=F/Ax/l
x=F×lAY if αs>αa
F×l0AYS=l0(1+αSΔθ)−1 ..(i)
ZF×l0AYa=l−l0(α+αaΔθ)..(ii)
By soving (i) and (ii) we get
l=l0[1+αaYa+ZαSYSYa+ZYS]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Single Correct148videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.318videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
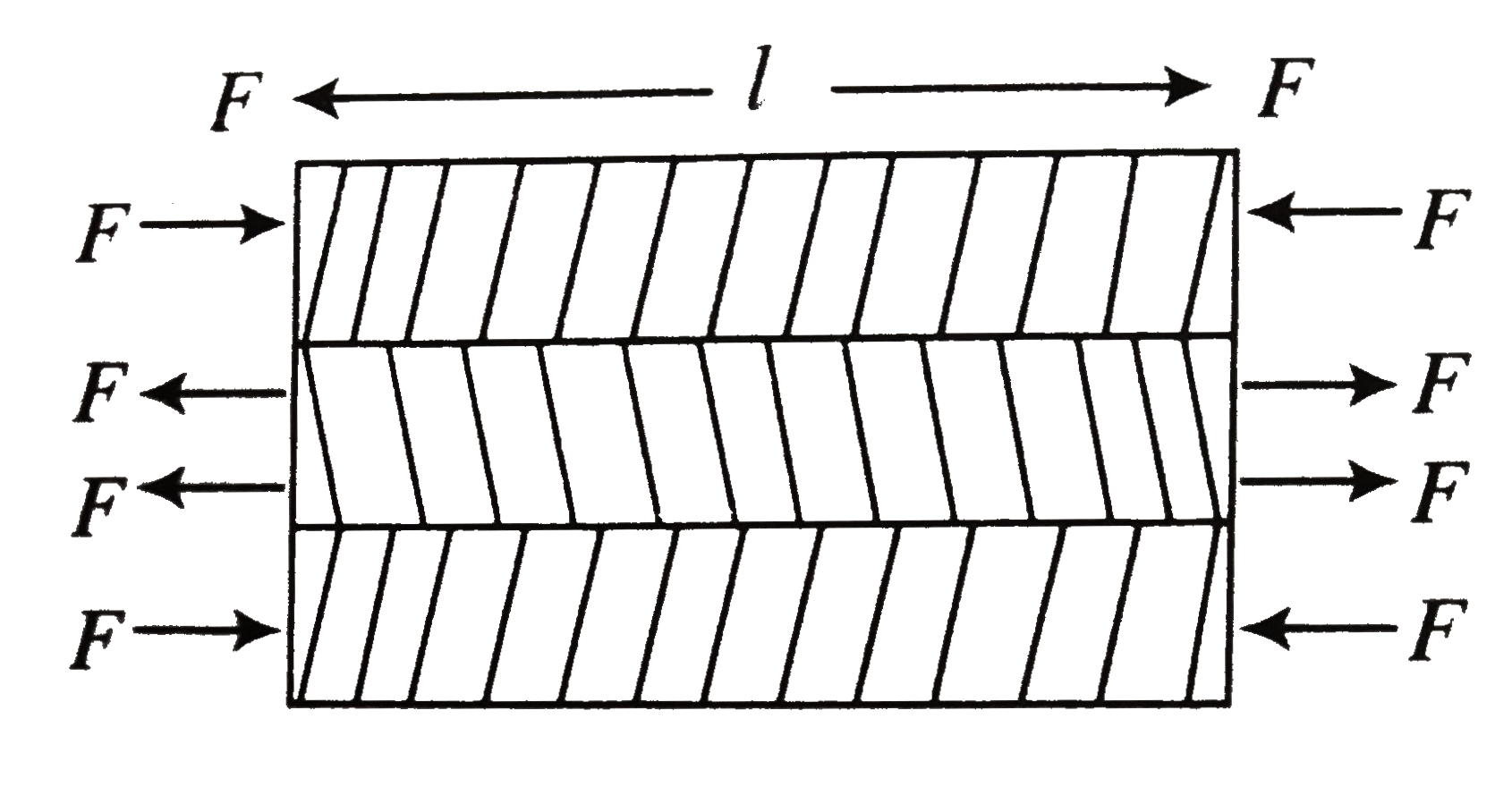
Two Aluminium rods and a steel rod of equal cross-sectional area and equal length l0 are joined rigidly side by side as shown in figure. Initially the rods are at 0∘C. Find the length of the rod at the temperature θ if young's modulus of elasticity of the aluminium and steel are Ya and Ys respectively and coefficient of linear expansion of aluminum and steel are αa and αs respectively.
∣∣ ∣∣AluminiumSteelAluminium∣∣ ∣∣View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
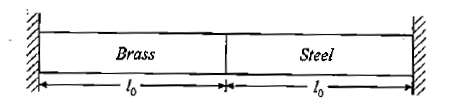 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22)) - Question 2 - Select One
Two rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
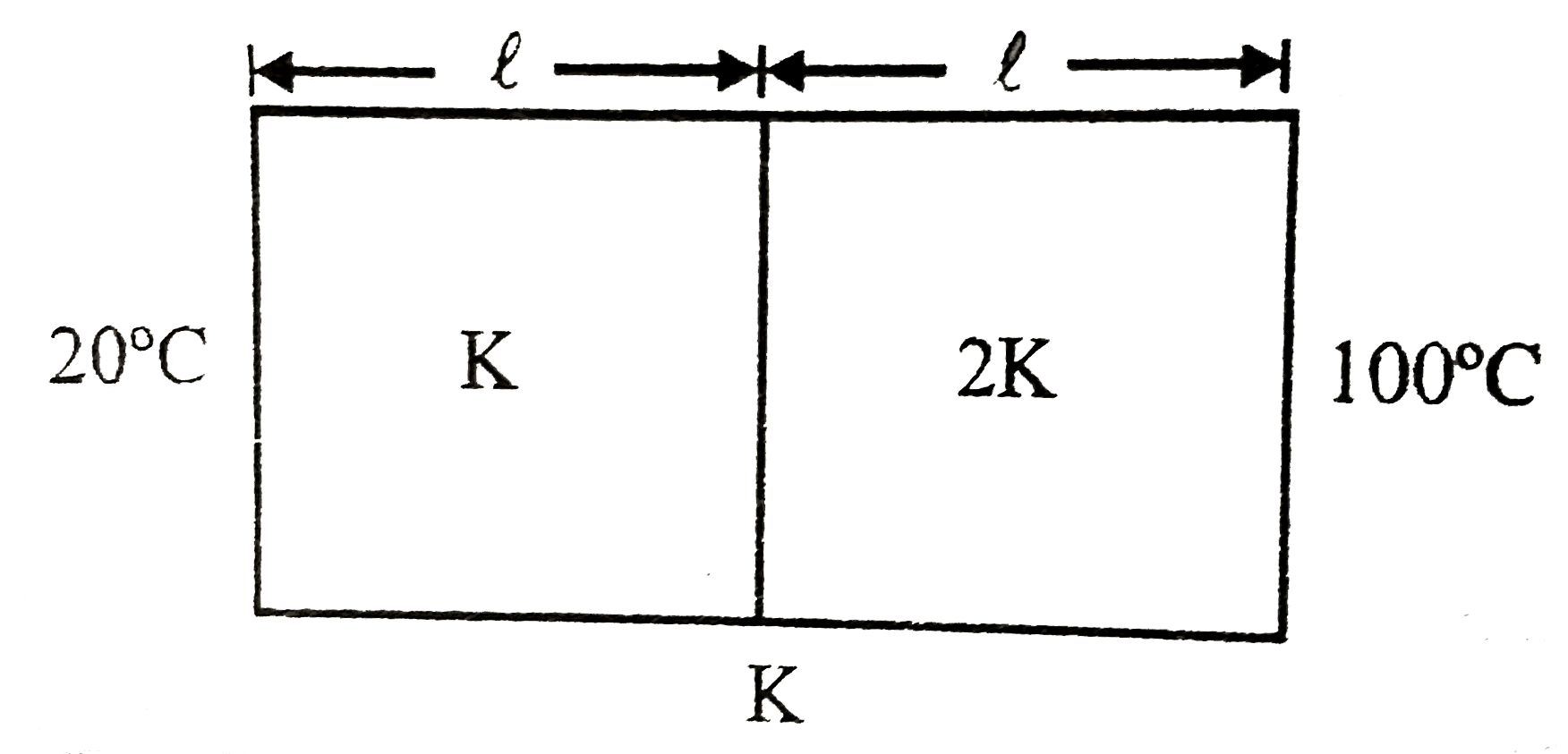 A60∘CB73.3∘CC46.7∘CD37.3∘C
A60∘CB73.3∘CC46.7∘CD37.3∘C - Question 3 - Select One or More
Two rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
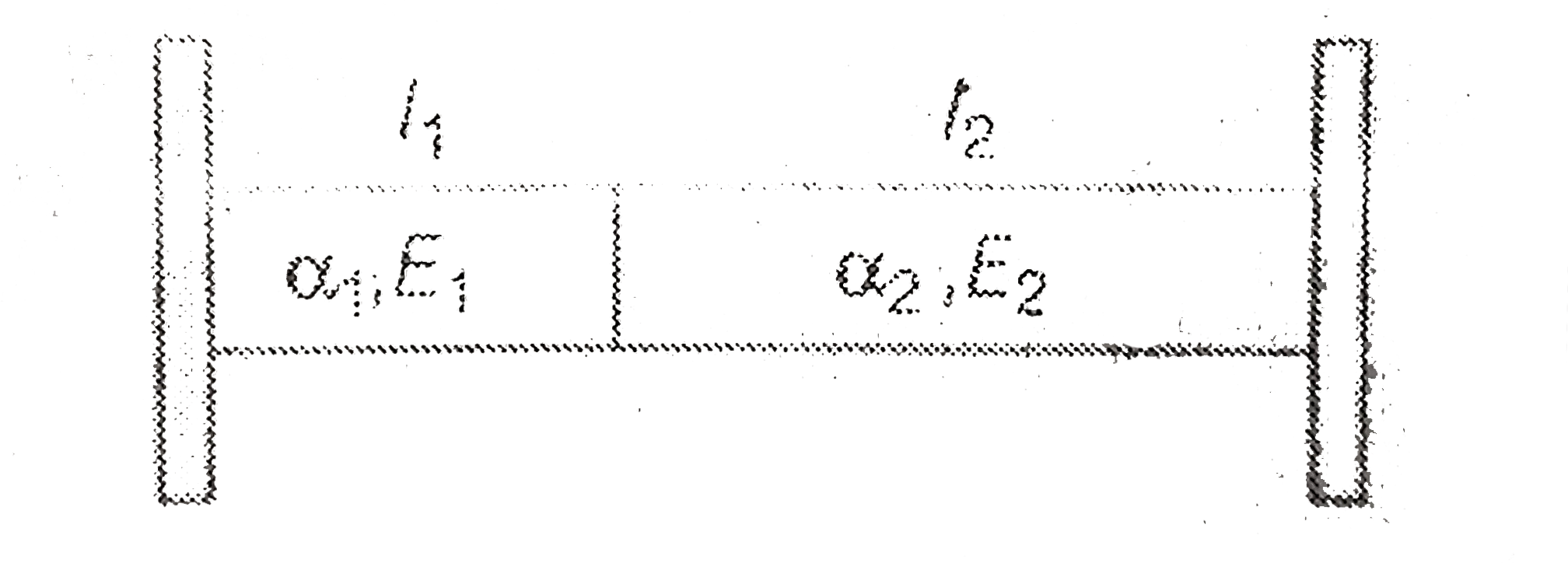 Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2
Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2
What should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionThere are two rods of length l1 l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.View SolutionA steel rod of length L0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through ΔT is (coefficient of linear expansion of steel is α and young's modulus for steel is Y ).
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remain constant at any temperature then
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_229_Q01.png)
If temperature of system is increased by ΔT then shifting in junction if junction if Y1α1>Y2α2 is given by -View Solution

