A vertical spring carries a 5kg body and is hanging in equilibrium an additional force is applied so that the spring is further stretched. When released from this position. It performs 50 complete oscillation in 25 s, with an amplitude of 5 cm. The additional force applied is
80 N
80π2N
4π2N
4N
The correct Answer is:C
T=2550=12s⇒ω=2πT=4πrads
Spring constant k=mω2=5×(4π)2=80π2Nm
Force required to stretch the spring by 5 cm is
F=kx=80π2×0.05N=4π2
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
View SolutionA spring is stretched by 5cm by a force 10N. The time period of the oscillations when a mass of 2Kg is suspended by it is
View Solution
Knowledge Check
A vertical spring of force cosntant 100N/m is attached with a hanging mass of 10 kg. Now an external force is applied on the mass so that the spring is stretched by additional 2m. The work done by the force F is (g=10m/s2)
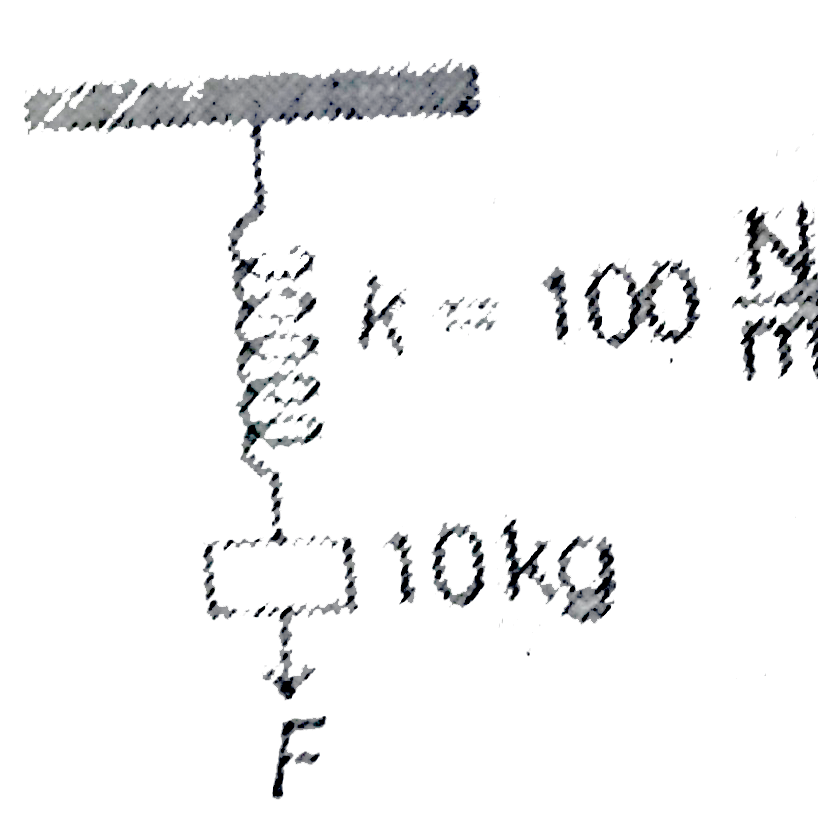A200 JB400 JC450 JD600 JA mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
A3.1cmB6.2cmC9.3cmD12.4cmA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
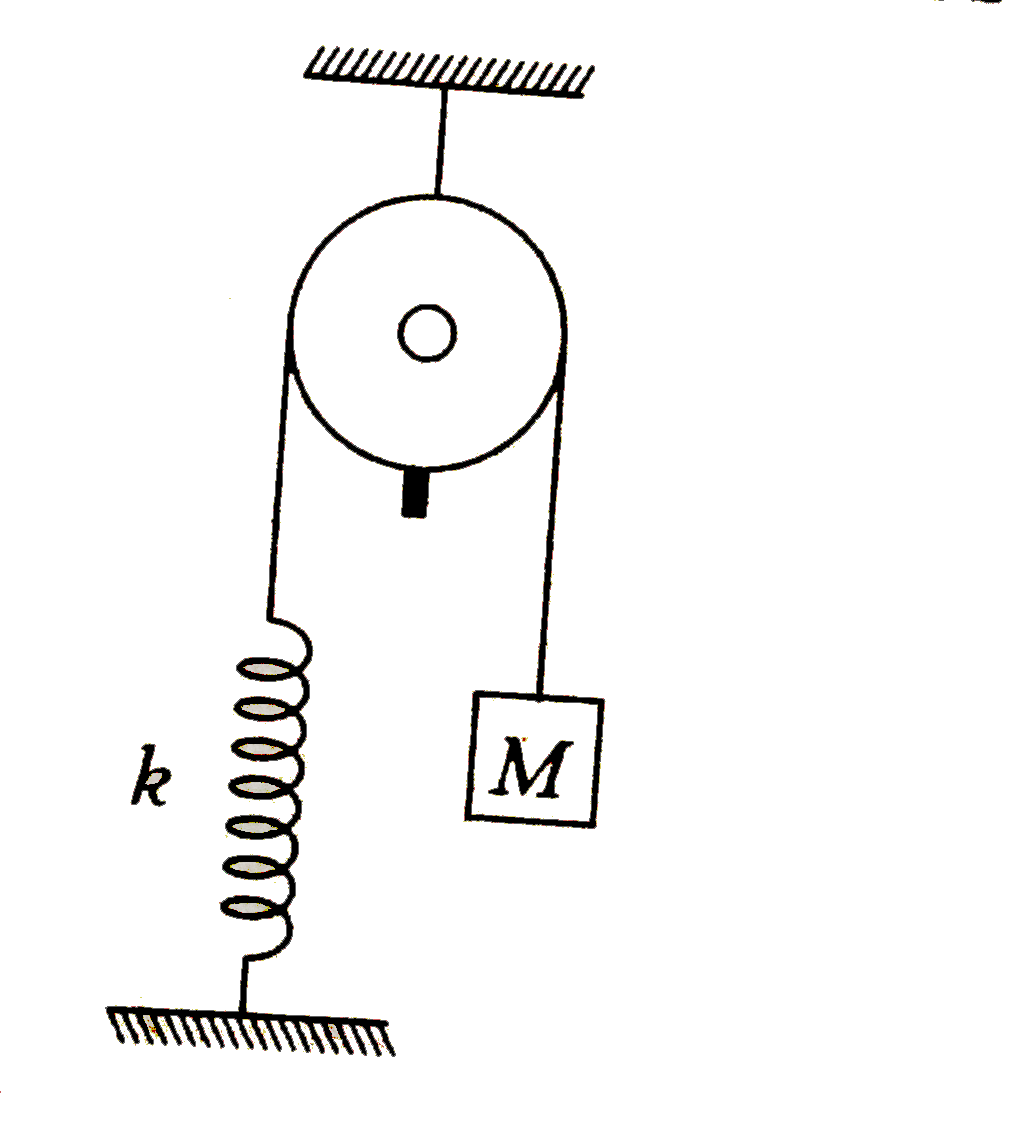A0.5 mB0.25 mC0.2 mD0.1 m
A 4-kg block extends a spring by 16 cm from its unstretched postion .The block is removed and a 0.5 -kg boby is hung from the same spring If the spring is then stretched and released , what is the time period of oscillations of the mass suspendrd ? What is the force constant of the spring ?
View SolutionA spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
View SolutionThe length of a spring is α when a force of 4N is applied on it and the length is β when 5N is applied. Then the leng of spring when 9N force is applied is-
View SolutionWhen a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
View SolutionWhen a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
View Solution