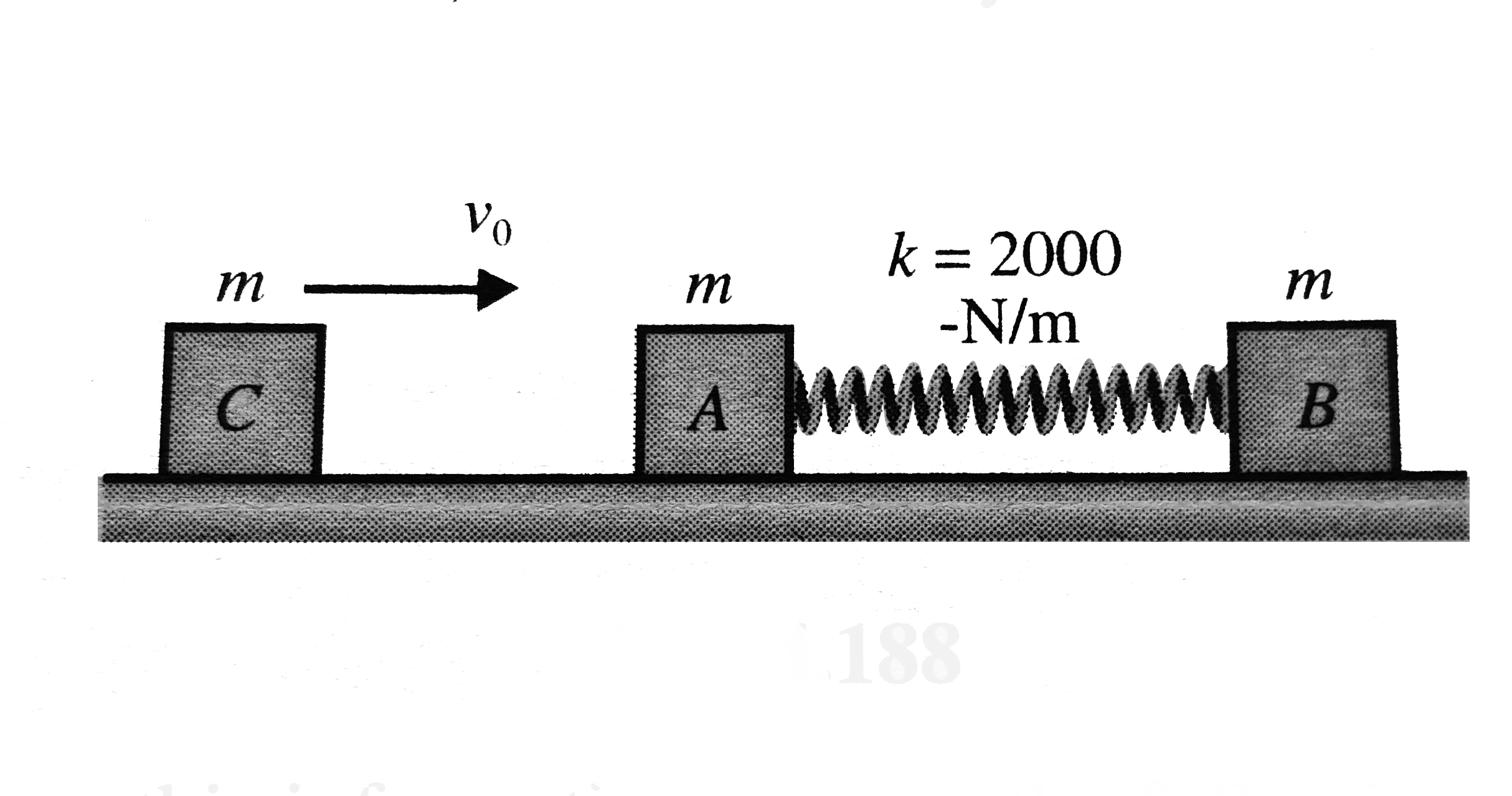
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. After the collision of C and A, the combined body and block B would
oscillate about centre of mass of system and centre of mass is at rest.
oscillate about centre of mass of system and centre of mass is moving.
oscillate but about different location other than the centre of mass.
not oscillate.
The correct Answer is:B
As C collides with A and sticks to its, the combined mass moves rightwards to compress the spring and hence B moves rightwards due to the spring force, i.e., B accelerates and the combined mass decelerates. The deformation in the spring is changing and the centre of mass of the system continues to move rightwards with contant speed, while both the blocks oscillate about centre of mass of the system.
The velocity of the combined mass just after collision is
mv0=2mv
v=v02=0.3ms
Velocity of centre of mass of system.
vCM=2mv+03m=2v3=v03=0.2ms
time period with which block B and the combined mass oscillate about centre of mass could be computed by using the reduced mass concept.
T=2π√2m3k=π5√10s
Oscillation energy of the system is
E=2mv22=0.27J
the translational kinetic energy of the centre of mass of system is
ECM=3mv22=0.18J
The remaining energy is oscillating between kinetic and potential energy during the motion of blocks. For maximum compression in spring either we can use cantre of mass approach or energy approach, here we are using the second method.
Oscillation energy = Maximum elastic potential energy
0.09=12kx2m⇒xm=3√10mm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Integer
Explore 10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
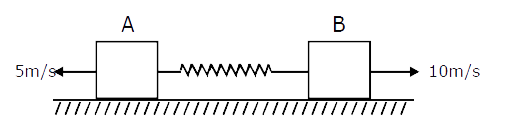
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
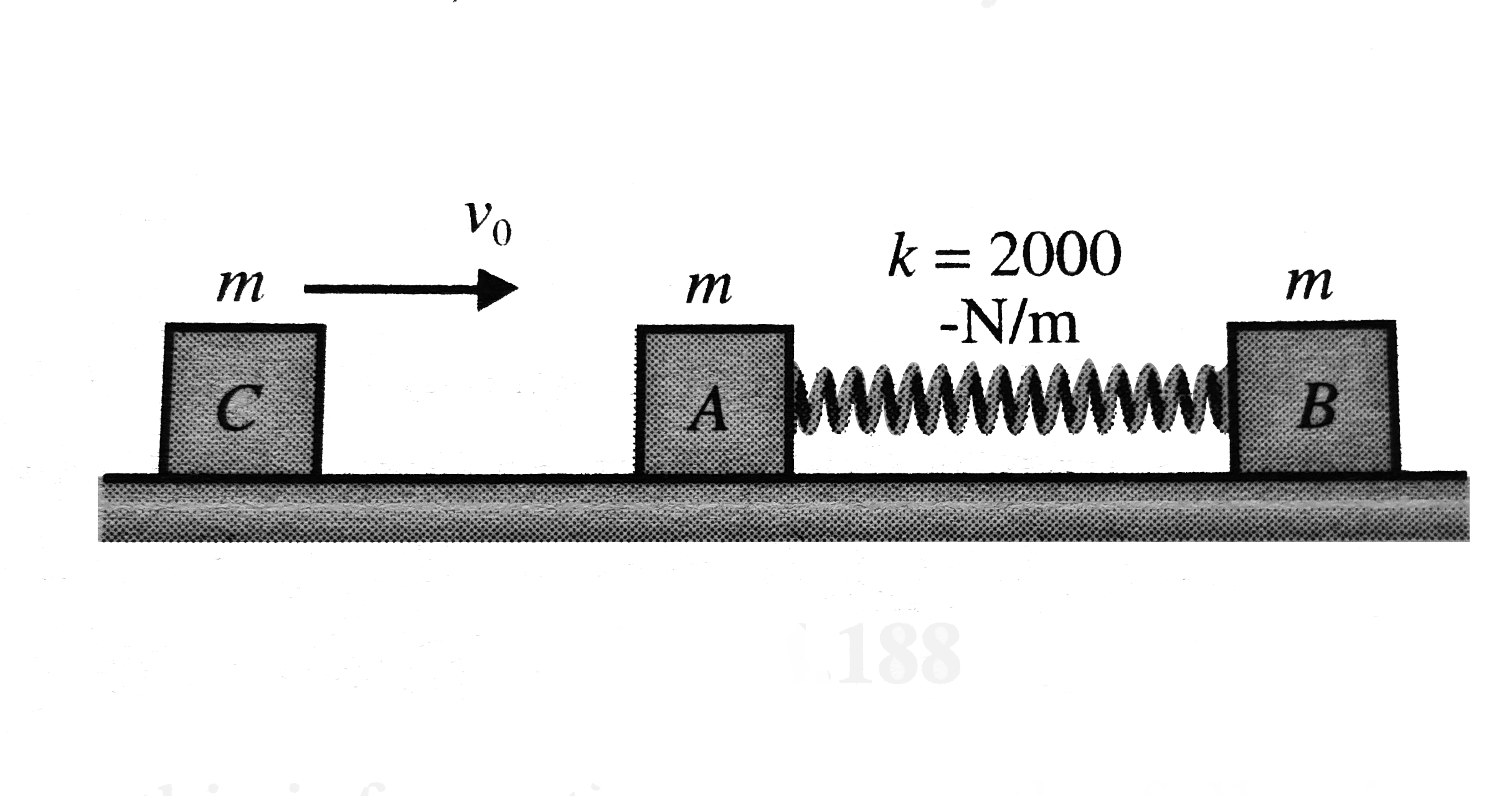
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. The maximum compression of the spring isA3√30mmB3√20mmC3√10mmD3√50mm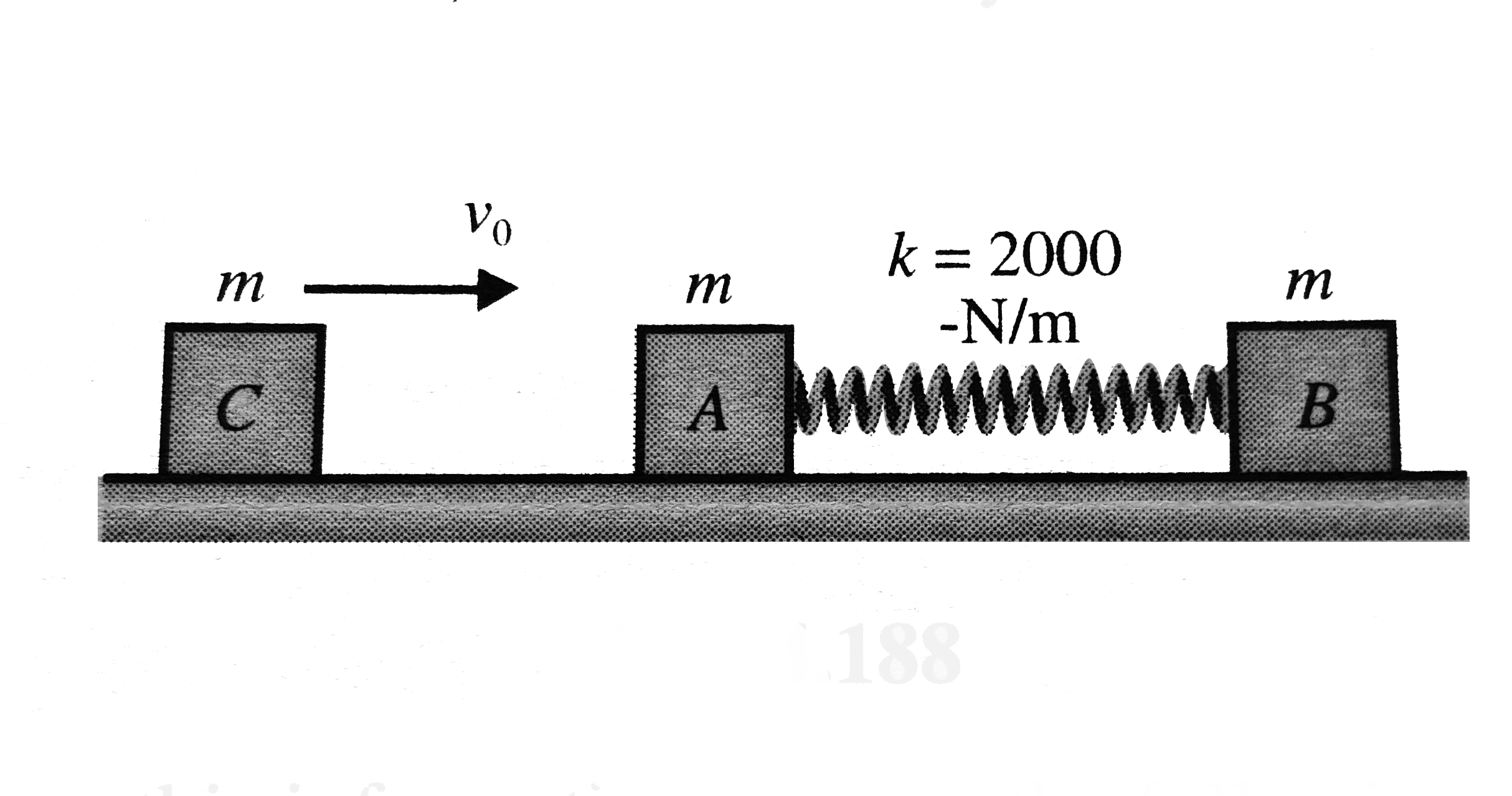
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. Oscillation energy of the system i.e., part of the energy which is oscillation (changing) between potention and kinetic forms isA0.27 JB0.09 JC0.18 JD0.45 JTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Two identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA block of mass m = 1 kg is placed over a plank Q of mass M = 6 kg, placed over a smooth horizontal surface as shown in figure. Block P is given a velocity v=2m/s2 to the right. If the coefficient of friction between P and Q is μ=0.3. Find the acceleration of Q relative to P.

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

View Solution
