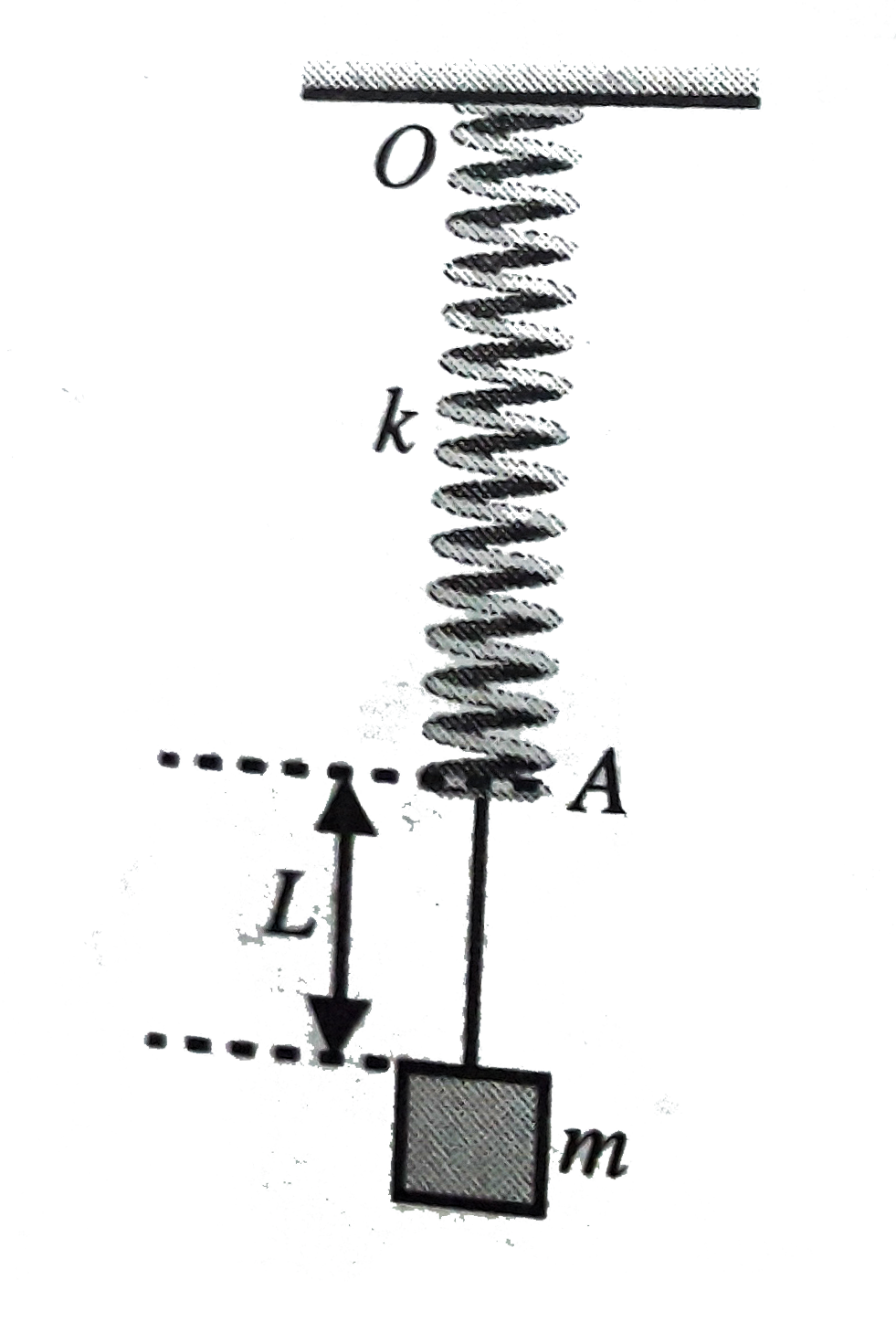
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
L
mgk
mgk√1+2kLmg
mgk[1+√1+2kLmg]
The correct Answer is:D
Let x be the maximum extension of the spring. The mass falls from rest through the vertical is Ek=mg(L+x). This must be stored in the spring as elastic energy at tis maximum extension Hence Ek=12kx2=mg(L+x)
This is quadratic, x2−2mgkx2mgLk=0
Hence, x=2mgk±√(2mgk)2+8mgLk2
Maximum value of x=mgk+mgk√1+2kLmg
=mgk(1+√1+2kLmg)
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion isAmg2kBmgkC2mg3kDLA body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
If the mass m, from the initial position of rest is pulled down a distance A and then released, assuming that the string remains taut throughout the motion, the maximum (downwards) acceleration of the oscillating body will beAkAmBkA2mCg2DgFor a body of mass m attached to the spring the spring factor is given by
Am/ω2Bmω2Cm2ωDm2ω2
A stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
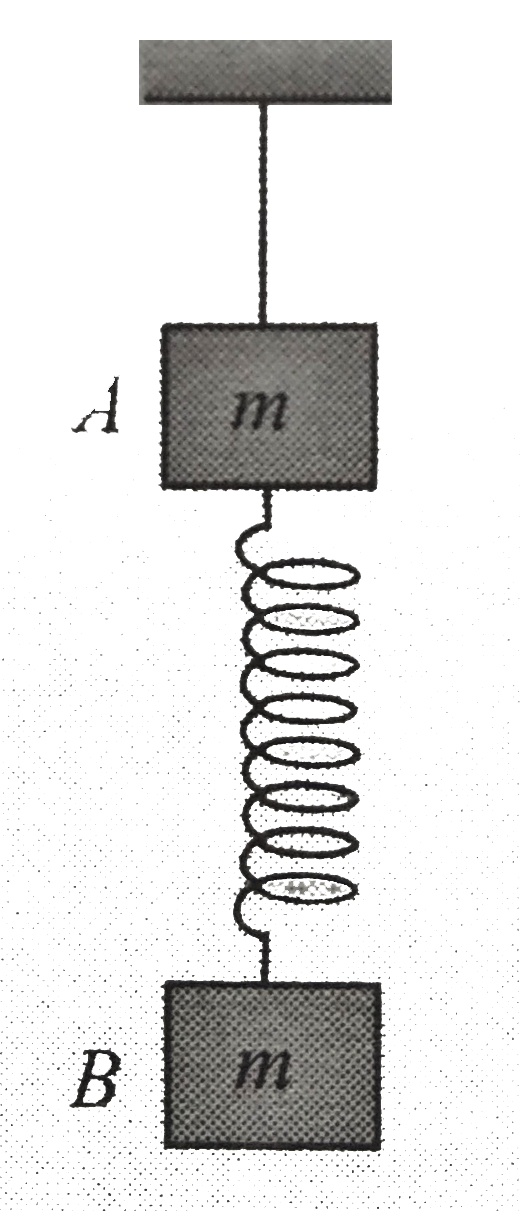
View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View Solution
