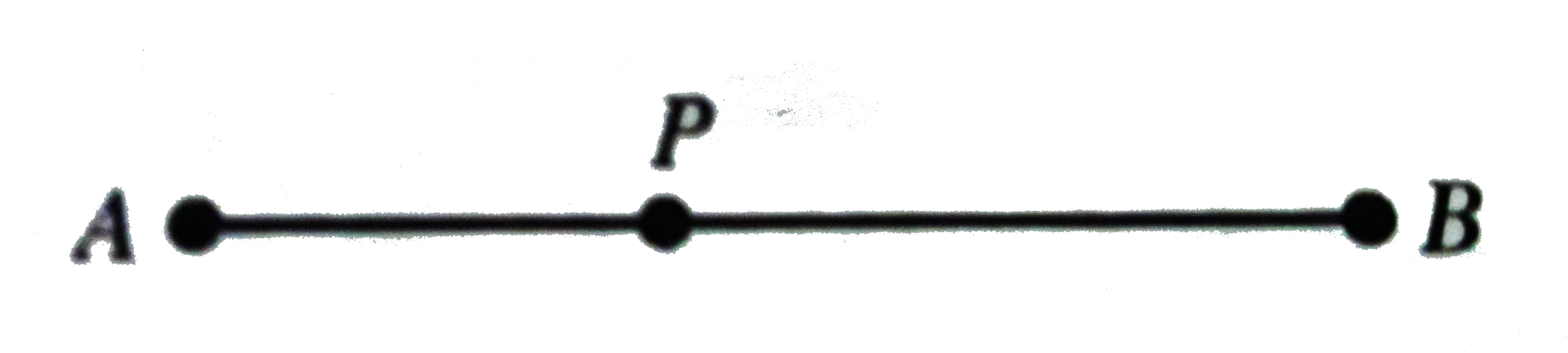
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB sumultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. Tha particle moves simple harmonically with period T and amplitude A.
A=2l,T=2π√lg
A=3l,T=2π√l2g
A=2l,T=2π√l3g
A=l,T=2π√lg.
The correct Answer is:C

Take x axis along AB and origin at A.
let AP=x, then PB=(3l−x)
The force on the particle of mass m at P is →F given by
→F=2(mgl)(−→x)+mgl(3l−xx)→x
=(3mg−3mglx) directed towards A
=3mgl(l−x) directed towards A
Hence equation of motion of mass m is
md2xdt2=−3mgl(l−x)=mω2(l−x)
where ω2=3gl
This is a simple harmonic motion of period T=2π√l2g.
The mean position is at the point x=l (i.e.) at O where AO=l.
Now for point A displacement =−l and hence
v2A=ω2(a2−(−l)2)=ω2(a2−l2)
where v2A=ω2(a2−(−l)2)=ω2(a2−l2) and a is the amplitude.
now nA=√gl (given) and hence v2A=9gm=3gl(a2−l2)
a2=4l2 or a=2l
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer10videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type2videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle of mass m is constrained to move along a straight line. A and B are two fixed points on the line at a separation of L. When the particle is at some point P, between A and B, it is acted upon by two forces
→F1=(6mgL)→PA and →F2=(3mgL)→PB
At time t=0, the particle is projected from A toward B with a speed of √gL.
At what time 't' will the particle reach at B for the first time ?
 View Solution
View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation isView Solution
Knowledge Check
- Question 1 - Select One
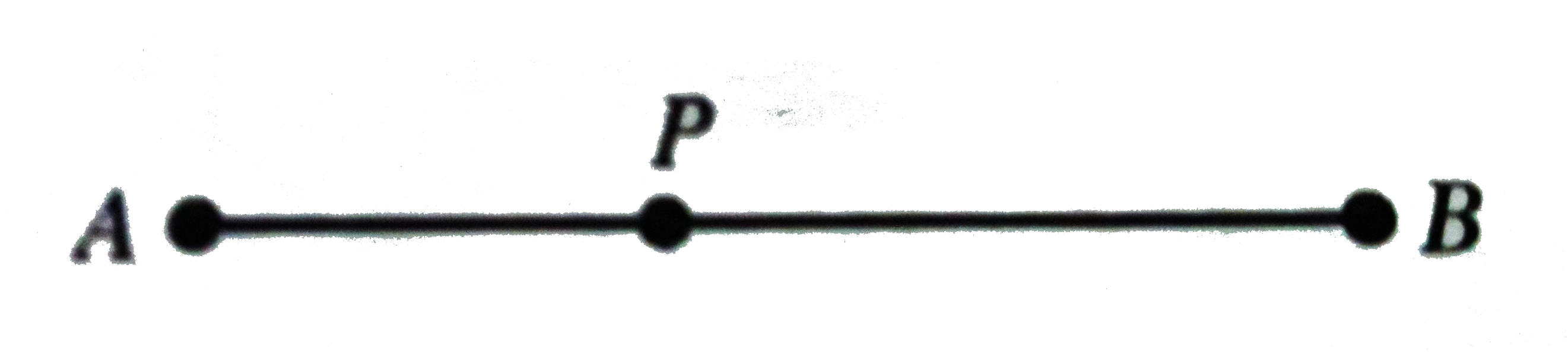
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB sumultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. The velocity of the particle when it reaches B will beAzeroB3√glC2√glD√gl - Question 2 - Select One
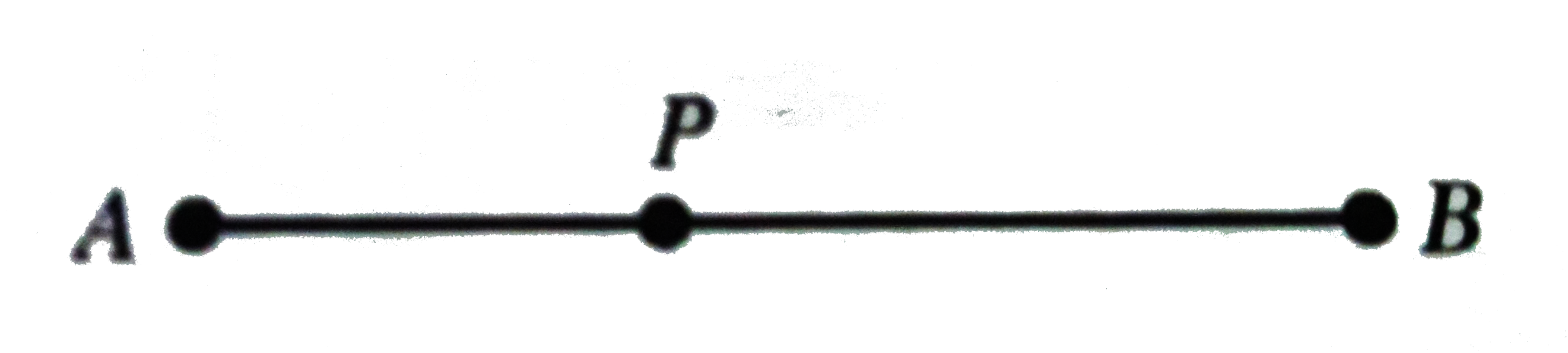
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB sumultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. The instant t at which the particle arrives at B in terms of the periodic time T will beAt=T2Bt=T3Ct=T4Dt=2T3 - Question 3 - Select One
A particle of mass m=5g is executing simple harmonic motion with an amplitude 0.3 m and time period π2 sec. The maximum value of force acting on the particle is
A5 NB4 NC0.5 ND0.15 N
Two particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
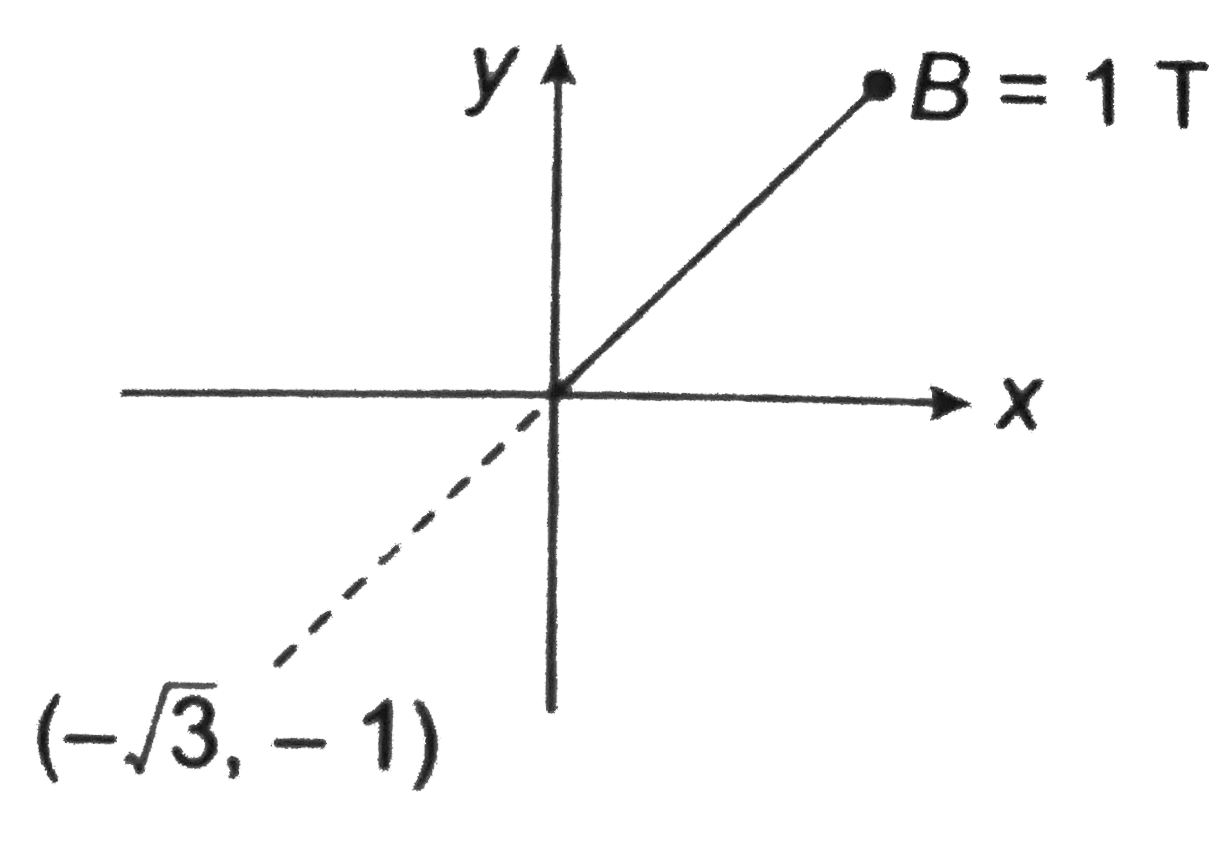
View SolutionA uniform magnetic field of magnitude 1T exists in region y≥0 along ˆk direction as shown. A particle of charge 1C is projected from point (−√3,−1) towards origin with speeds 1m/sec. If mass of particle moves are:
 View Solution
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.View SolutionA point particle is acted upon by a restoring force –kx3 . The time period of oscillation is T when the amplitude is A. The time period for an amplitude 2A will be :
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find the minimum distance of the particle from B during the motion.View Solution

