ABCD is a rectangle (Fig. 11.31) in which DP and BQ are perpendiculars from D and B respectively on diagonal AC. Show that(1) ΔADP=ΔACBQ (ii) ∠ADP=∠CBQ(iii) DP = BQ
Step by step video & image solution for ABCD is a rectangle (Fig. 11.31) in which DP and BQ are perpendiculars from D and B respectively on diagonal AC. Show that(1) Delta ADP = Delta ACBQ (ii) /_ADP = /_CBQ(iii) DP = BQ by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
In Figure, ABCD is a rectangle. BM and DN are perpendicular from B and D respectively on AC . Prove that MBC≅DNA (ii) BM=DN
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An isosceles ΔABC is right angled at B. D lies inside ΔABC. P and Q are resectively the base of perpendiculars drawnon side AB and AC of ΔABC from point D. If AP = a cm, AQ = b cm and ∠BAD=15∘, then what will be sin75∘?
A2b√3aBa2bC√3a2bD2a√3b - Question 2 - Select One
An isosceles triangle ABC is right angled at B.D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the sides AB and AC respectively of ΔABC. If AP = a cm, AQ = b cm and ∠BAD=15∘,sin75∘=
A2b√3aBa2bC√(3)(a)2bD2a√3b
ABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View SolutionIn an adjoining figure, ABCD is a rectangle, BM and DN are perpendicular from B and D on AC (i) Is ΔBMC=ΔDNA
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
 View Solution
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
 View Solution
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
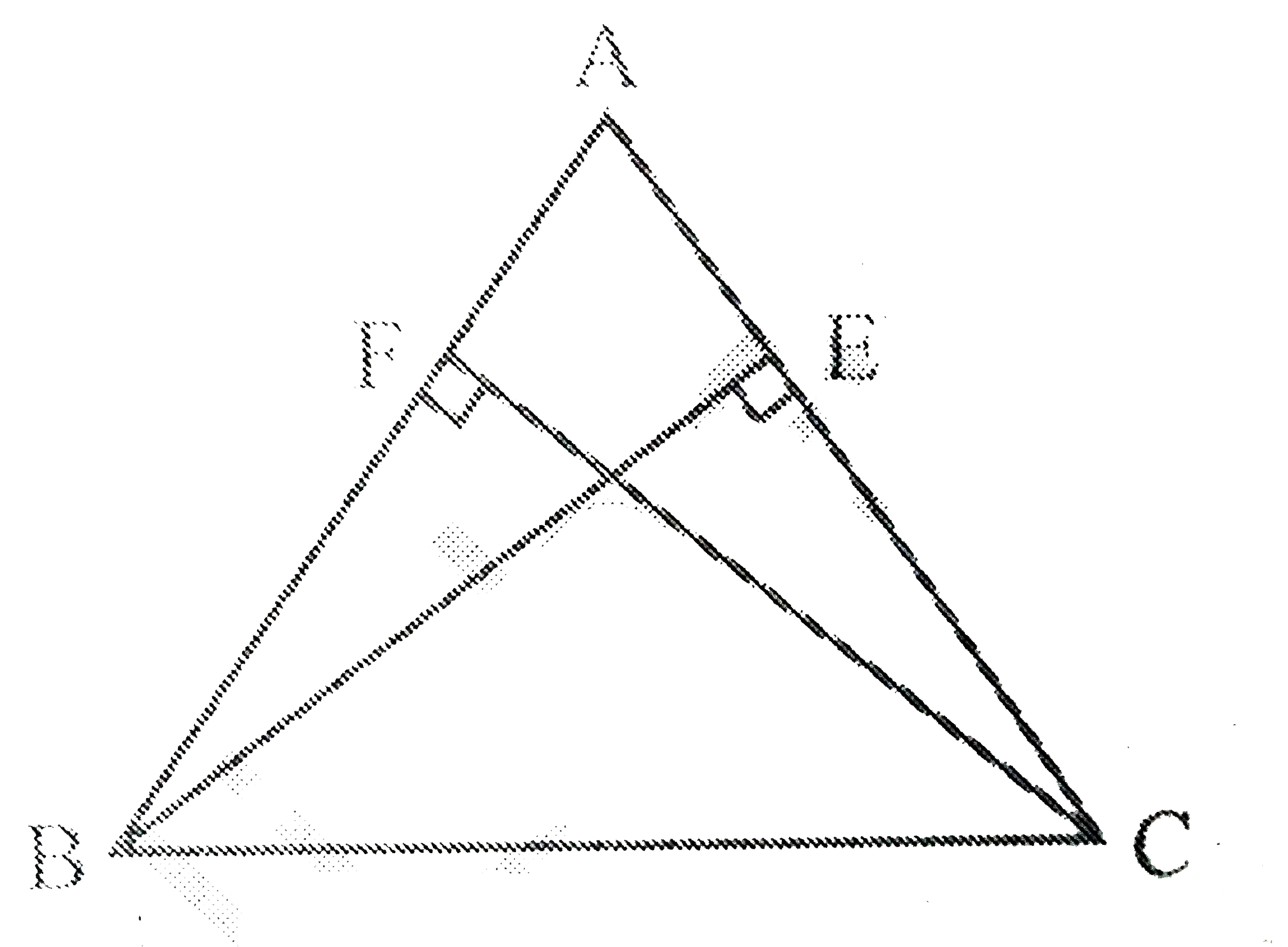 View Solution
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
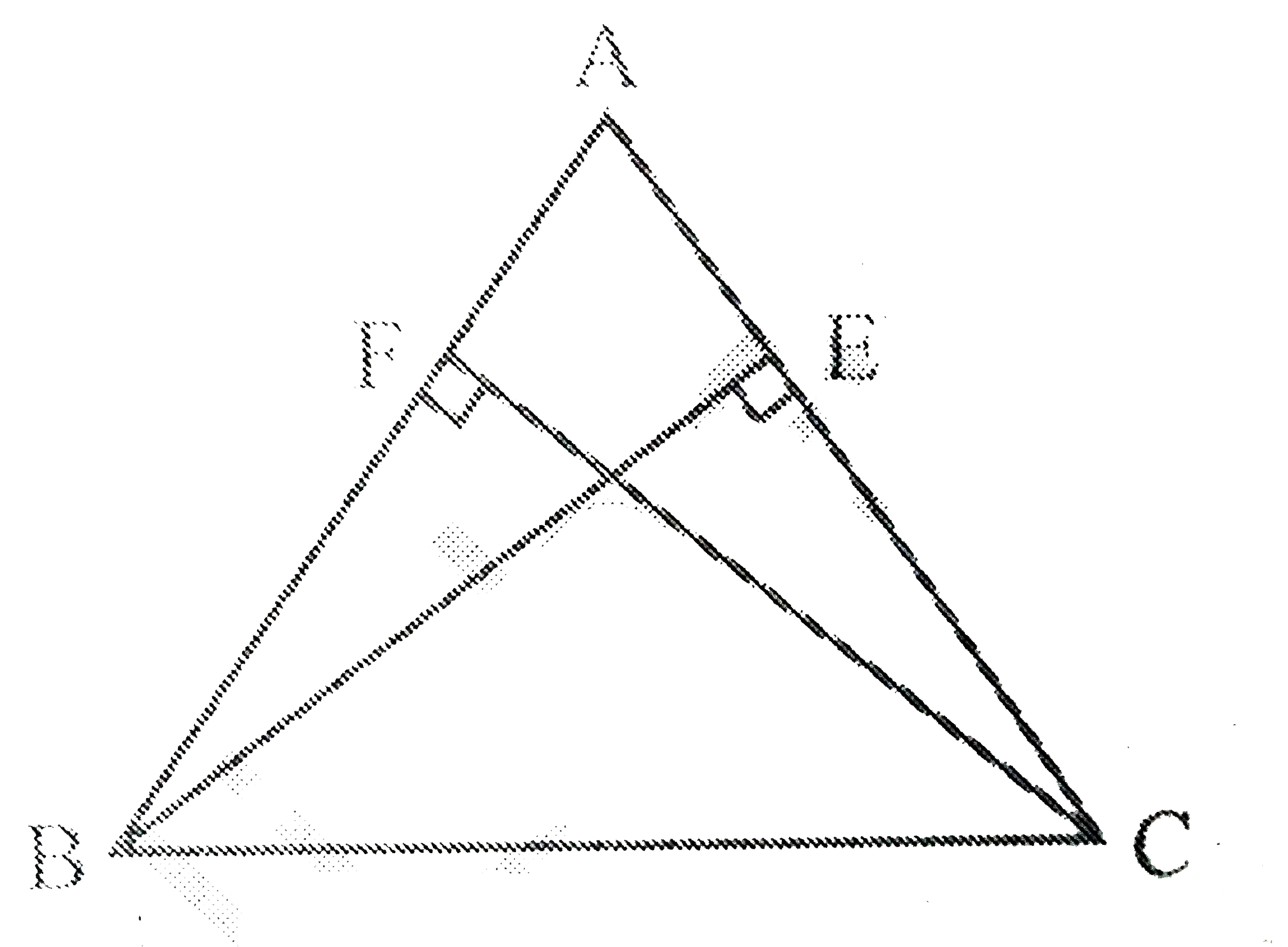 View Solution
View Solution

