A frog walking in a narrow lane takes 5 leaps forward and 3 leaps backward, then again 5 leaps forward and 3 leaps backward, and so on. Each leap is 1m long and requires 1s. Determine how long the frog takes to fall in a pit 13m away from the starting point.
35 s
36 s
37 s
38 s
The correct Answer is:C
To determine how long the frog takes to fall into a pit that is 13 m away from the starting point, we can analyze the frog's movement step by step.
Step 1: Understand the frog's movement pattern
The frog takes 5 leaps forward and then 3 leaps backward. Each leap is 1 meter long and takes 1 second.
Step 2: Calculate the net distance covered in one complete cycle
In one complete cycle:
- The frog moves forward 5 meters.
- Then, it moves backward 3 meters.
Net distance covered in one cycle = Distance forward - Distance backward
= 5 m - 3 m = 2 m.
Step 3: Determine the time taken for one complete cycle
The time taken for one cycle consists of:
- Time for 5 leaps forward = 5 leaps × 1 second/leap = 5 seconds.
- Time for 3 leaps backward = 3 leaps × 1 second/leap = 3 seconds.
Total time for one cycle = Time forward + Time backward
= 5 seconds + 3 seconds = 8 seconds.
Step 4: Calculate how many cycles are needed to reach or exceed 13 m
To find out how many complete cycles the frog needs to reach or exceed 13 m, we divide the total distance by the net distance covered in one cycle.
Number of complete cycles = Total distance / Net distance per cycle
= 13 m / 2 m = 6.5 cycles.
Since the frog cannot complete half a cycle, we will consider 6 complete cycles first.
Step 5: Calculate the distance covered in 6 complete cycles
Distance covered in 6 complete cycles = Number of cycles × Net distance per cycle
= 6 cycles × 2 m/cycle = 12 m.
Step 6: Calculate the time taken for 6 complete cycles
Time taken for 6 complete cycles = Number of cycles × Time per cycle
= 6 cycles × 8 seconds/cycle = 48 seconds.
Step 7: Determine the remaining distance to the pit
After 6 complete cycles, the frog is at a distance of 12 m from the starting point. The pit is at 13 m, so the remaining distance to the pit is:
Remaining distance = 13 m - 12 m = 1 m.
Step 8: Calculate the time taken to cover the remaining distance
To cover the remaining distance of 1 m, the frog will take 1 leap forward, which takes 1 second.
Step 9: Calculate the total time taken to reach the pit
Total time taken = Time for 6 complete cycles + Time for the last leap
= 48 seconds + 1 second = 49 seconds.
Final Answer
The frog takes a total of 49 seconds to fall into the pit that is 13 m away from the starting point.
---
The frog takes 5 leaps forward and then 3 leaps backward. Each leap is 1 meter long and takes 1 second.
In one complete cycle:
- The frog moves forward 5 meters.
- Then, it moves backward 3 meters.
= 5 m - 3 m = 2 m.
The time taken for one cycle consists of:
- Time for 5 leaps forward = 5 leaps × 1 second/leap = 5 seconds.
- Time for 3 leaps backward = 3 leaps × 1 second/leap = 3 seconds.
= 5 seconds + 3 seconds = 8 seconds.
To find out how many complete cycles the frog needs to reach or exceed 13 m, we divide the total distance by the net distance covered in one cycle.
= 13 m / 2 m = 6.5 cycles.
Distance covered in 6 complete cycles = Number of cycles × Net distance per cycle
= 6 cycles × 2 m/cycle = 12 m.
Time taken for 6 complete cycles = Number of cycles × Time per cycle
= 6 cycles × 8 seconds/cycle = 48 seconds.
After 6 complete cycles, the frog is at a distance of 12 m from the starting point. The pit is at 13 m, so the remaining distance to the pit is:
Remaining distance = 13 m - 12 m = 1 m.
To cover the remaining distance of 1 m, the frog will take 1 leap forward, which takes 1 second.
Total time taken = Time for 6 complete cycles + Time for the last leap
= 48 seconds + 1 second = 49 seconds.
The frog takes a total of 49 seconds to fall into the pit that is 13 m away from the starting point.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Motion With Constant Acceleration30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Motion Under Gravity30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test29videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test29videos
GRAVITATION
Similar Questions
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, and again takes 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Determine how long the drunkard takes to fall into a pit 13 m away from the start.
View SolutionA drunkard waking in a barrow lane takes 5 steps forward and 3 steps backward, followed again 5 steps forward and 3 steps backward, and so on. Each step is 1mlong and requires 1 s.Determinehowlongthedrunkardtakes→fall∈aπt 13 m away from start.
View Solution
Knowledge Check
- Question 1 - Select One
A drunkard is walking along a stsraight road. He takes five steps forward and three steps backward and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m, away from the starting point. The drunkard will fall into the pit after.
A29sB21sC37sD31s - Question 2 - Select One
A boy starts from home in early morning and walks straight for 8 km facing the Sun. Then he takes a right turn and walks for 3 km. Then he turns right again and walks for 2 km and then turns left and walks for 1 km. Then he turns right, travels 1 km and then turns right and travels for 4 km straight. How far is he from the starting point ?
A4 kmB5 kmC6 kmD2 km
A drunkard waking in a borrow lane takes 6 steps forward and 4 steps backward, following againg 6 steps forward and 4 steps backward and so on Each step is 1m long and requires 1s. Determine how long the drunkard takes to fall in a pit 15m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x−t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1s. Plot the x-t graph of his motion. Determine graphically or otherwise how long the drunkard takes to fall in a pit 9 m away from the start.
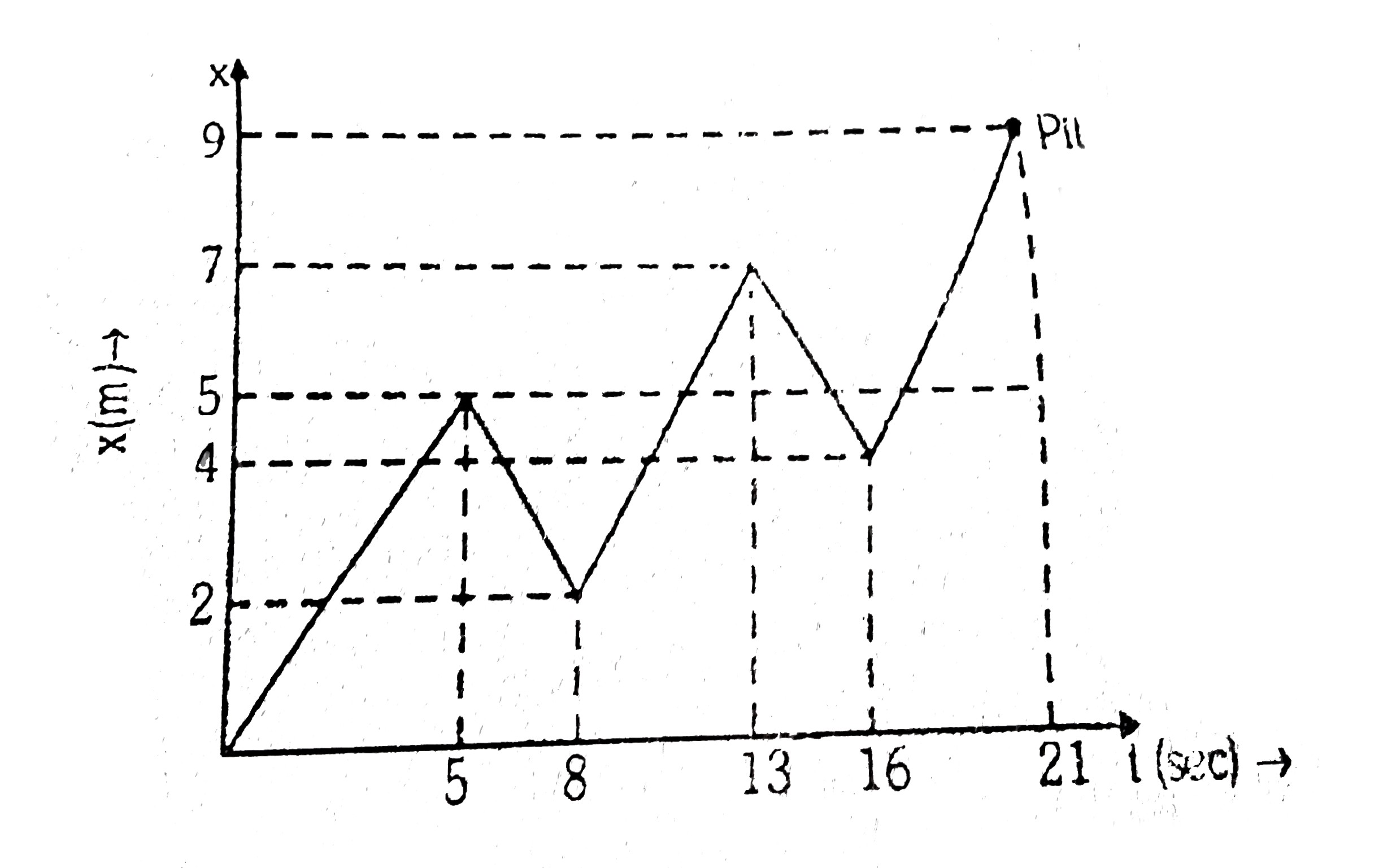 View Solution
View SolutionA drunkard man walking in a narrowlane takes (5) steps forward and 3 steps backward each stepe of (1) m ling, per second and os on. Determine how long the drunkard takes to fall in a pot 15m away from the start.
View SolutionA man takes a step forward with probability 0.4 and backward with probability 0.6. Find the probability that at the end of 5 steps, he is one step away from the starting point.
View SolutionA drunkard moves on a straight road such that he takes 7 steps forward and 2 steps backward in each cycle. If the stride length of each step is 1 feet and the drunkard moves with a speed 2 feet/s in forward direction and 4 feet/s in backward direction, then the time after which the drunkard will fall into a pit 11 feet further from his starting point is
View Solution

