A body of mass M at rest explodes into three pieces, two of which of mass M//4 each are thrown off in prependicular directions eith velocities of 3/s and 4m/s respectively. The third piece willl be thrown off with a velocity of
1.5m/s
2.0m/s
2.5m/s
3.0m/s
The correct Answer is:C
To solve the problem step by step, we will use the principle of conservation of momentum.
Step 1: Understand the problem
A body of mass M explodes into three pieces. Two pieces have masses M4 each and are thrown off in perpendicular directions with velocities 3m/s and 4m/s respectively. We need to find the velocity of the third piece.
Step 2: Set up the momentum conservation equation
Since the body is initially at rest, the total initial momentum is zero. Therefore, the total final momentum must also equal zero.
Let:
- P1 be the momentum of the first piece,
- P2 be the momentum of the second piece,
- P3 be the momentum of the third piece.
The momentum of each piece can be calculated as:
- P1=M4×3 (in the x-direction)
- P2=M4×4 (in the y-direction)
Step 3: Calculate the momenta of the first two pieces
Calculating P1 and P2:
- P1=M4×3=3M4 (in the x-direction)
- P2=M4×4=4M4=M (in the y-direction)
Step 4: Find the resultant momentum of the first two pieces
Since P1 and P2 are perpendicular, we can find the resultant momentum PR using the Pythagorean theorem:
PR=√P21+P22=√(3M4)2+(M)2
Calculating this gives:
PR=√9M216+M2=√9M216+16M216=√25M216=5M4
Step 5: Set up the equation for the third piece
Since the total momentum must equal zero, the momentum of the third piece P3 must equal the negative of the resultant momentum of the first two pieces:
P3=−PR=−5M4
The mass of the third piece is:
M3=M−M4−M4=M2
Thus, the momentum of the third piece can be expressed as:
P3=M2×v3
Setting the two expressions for P3 equal gives:
M2×v3=−5M4
Step 6: Solve for the velocity of the third piece
Dividing both sides by M2:
v3=−5M4×2M=−52=−2.5m/s
The negative sign indicates the direction of the velocity is opposite to the resultant momentum of the first two pieces.
Final Answer
The velocity of the third piece is 2.5m/s in the opposite direction.
---
A body of mass M explodes into three pieces. Two pieces have masses M4 each and are thrown off in perpendicular directions with velocities 3m/s and 4m/s respectively. We need to find the velocity of the third piece.
Since the body is initially at rest, the total initial momentum is zero. Therefore, the total final momentum must also equal zero.
- P1 be the momentum of the first piece,
- P2 be the momentum of the second piece,
- P3 be the momentum of the third piece.
- P1=M4×3 (in the x-direction)
- P2=M4×4 (in the y-direction)
Calculating P1 and P2:
- P1=M4×3=3M4 (in the x-direction)
- P2=M4×4=4M4=M (in the y-direction)
Since P1 and P2 are perpendicular, we can find the resultant momentum PR using the Pythagorean theorem:
PR=√P21+P22=√(3M4)2+(M)2
Calculating this gives:
PR=√9M216+M2=√9M216+16M216=√25M216=5M4
Since the total momentum must equal zero, the momentum of the third piece P3 must equal the negative of the resultant momentum of the first two pieces:
P3=−PR=−5M4
The mass of the third piece is:
M3=M−M4−M4=M2
Thus, the momentum of the third piece can be expressed as:
P3=M2×v3
Setting the two expressions for P3 equal gives:
M2×v3=−5M4
Dividing both sides by M2:
v3=−5M4×2M=−52=−2.5m/s
The negative sign indicates the direction of the velocity is opposite to the resultant momentum of the first two pieces.
The velocity of the third piece is 2.5m/s in the opposite direction.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle19videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Applications Of Newton'S Laws Of Motion33videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
Similar Questions
A body of mass 4m at rest explodes into three pieces. Two of the pieces each of mass m move with a speed v each in mutually perpendicular directions. The total kinetic energy released is
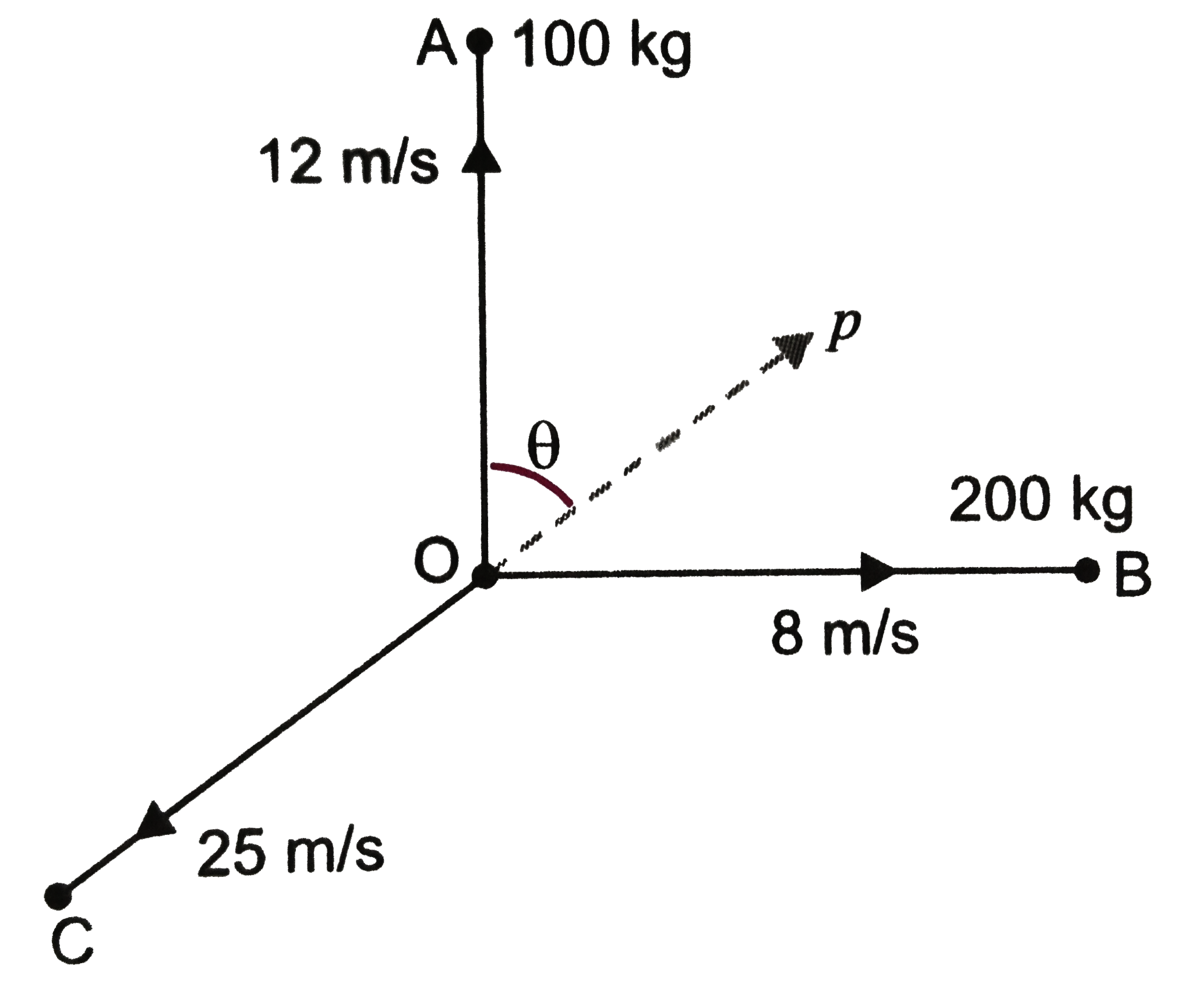
View SolutionAn explosion blows a rock into three pieces Two pieces whose masses are 200 kg and 100 kg go off at 90∘ to eachother with a velocity of 8m/s and 12m/s respectively If the third piece flies off with a velocity of25m/s then calculate the mass of this piece and indicate the direction of flight of this piece in a diagram.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body oa mass M at rest explodes into three pieces, two of which of mass (M/4) each are thrown- off in perpendicular directions with velocities of 6ms−1 and 8ms−1 respectively. The third piece will be thrown-off with a velocity of
A1.5ms−1B2ms−1C5ms−1D3ms−1 - Question 2 - Select One
A body of mass M at rest explodes into 3 pieces, A,B and C of masses M4,M4 and M2 respectively. A and B move in perpendicular directions with velocities 5m/s and 12 m/s respectively. What is the speed of the third piece?
A3.5m/sB5.5m/sC6.5m/sD8m/s - Question 3 - Select One
A body of mass 4m at rest explodes into three fragments. Two of the fragments each of mass m move with speed v in mutually perpendicular directions. Total energy released in the process is
Amv2B32mv2C2mv2D3mv2
A stationary body of mass 3 kg explodes into three equal pieces. Two of the pieces fly off in two mutually perpendicular directions, one with a velocity of 3ˆims1 and the other with a velocity of 4ˆjms−1 . - If the explosion occurs in 10–4s, the average force acting on the third piece in newton is
View SolutionA body of mass 1 kg at rest explodes into three fragments of masses in the ratio 1 : 1 : 3 . The two pieces of equal mass fly in mutually perpendicular directions with a speed of 30m/s each . What is the velocity of the heavier fragment ?
View SolutionA Diwali cracker of mass 60 g at rest, explodes into three pieces A, B and C of mass 10 g, 20 g and 30 g respectively. After explosion velocities of A and B are 30 m/s along east and 20 m/s along north respectively. The instantaneous velocity of C will be
View SolutionA bomb at rest explodes into three fragments of equal massses Two fragments fly off at right angles to each other with velocities of 9m/s and 12/s Calculate the speed of the third fragment .
View SolutionIf the velocities of three molecules are 2 m/s, 3 m/s, 4m/s respectively. Then the mean velocity will be
View Solution

